2.1.3 Обязательная (директивная) корреспонденция

Директивная корреспонденция означает обязательность поставки из точки Аi; в точку Вj части или всего объема груза, имеющегося в точке Аi, В этом случае величина обязательной поставки вычитается из суммы спроса Вj и суммы ограничения Аi и при решении задачи не учитывается.

Например, из точки А2 нужно обязательно поставить 400 т груза в В3 (Таблица 6). Следовательно, при решении задачи ограничения столбца В3 и строки А2 должны быть уменьшены на 400 т, т.е. будут равны для В3 - 400 т (800 - 400 = 400) и для А2 - 200 т (600 - 400 = 200).

При подсчете окончательного грузооборота обязательный объем (400*8 = 3200 т*км) прибавляют к полученному оптимальному объему грузооборота.

2.1.4 Открытая модель распределительного метода

Открытая модель распределительного метода возникает в тех случаях, когда отсутствует какая-либо из групп ограничений — спрос bj или предложение ai. Это означает, что любой потребитель может взять всю сумму имеющихся у поставщиков материалов или, наоборот, любой из поставщиков может удовлетворить спрос всех потребителей данного материала.

Задача решается просто. Если отсутствуют ограничения по предложению, то ограничения по спросу в каждом столбце таблицы переносятся в клетки с оптимальным элементом целевой матрицы данного столбца, а при отсутствии ограничений по спросу - в клетки каждой строки. Полученное решение всегда будет оптимальным.

Рассмотрим пример. Чтобы удовлетворить потребности в строительном песке пяти потребителей В1, В2, В3, В4, В5, его можно добывать в неограниченном количестве в любой из трёх точек А1, А2, А3. Потребность в сутки: В1 - 300 т, В2 - 200 т, В3 - 400 т, В4 – 250 т, В5 - 400 т.

Расстояния (элементы целевой матрицы) между потребителями и возможными местами добычи песка указаны в правых верхних углах клеток (Таблица 7) .Сколько в каждой точке нужно добывать песка и как спланировать грузопотоки, чтобы транспортная работа была оптимальной?

Таблица 7

Возможные поставщики песка	Потребители песка					Запасы, т
	B1	B2	B3	B4	B5
A1	2	4	6	3	4	--
A2	5	3	8	5	4	--
A3	3	1	4	5	3	--
Потребность, т	300	200	400	250	400	1550

Переносим ограничения спроса по столбцам в клетки с минимальными расстояниями А1В1, А3В2, А3В3, А1В4, А3В5. Таким образом, эти клетки получают загрузку в 300 т, 200 т, 400 т, 250 т и 400 т (табл. 19).

Таблица 8

Возможные поставщики песка	Потребители песка					Запасы, т
	B1	B2	B3	B4	B5
A1	2 300	4	6	3 250	4	550
A2	5	3	8	5	4	--
A3	3	1 200	4 400	5	3 400	1000
Потребность, т	300	200	400	250	400	1550

Поскольку загружались клетки с оптимальным значением элемента целевой матрицы, то полученное решение с точки зрения транспортной работы будет оптимальным. При этом добыча песка в точках А1 и А2 должна быть соответственно 550 и 1000 т. В точке А2 добычу вести нерационально.

Открытая модель распределительного метода встречается при решении задач определения оптимального размещения и мощности АТП, закрепления маршрутов за АТП, размещения и ёмкости складов.

2.2 Решение транспортной задачи методом запрещения корреспонденции.

Грузообразующие точки (три мельницы) имеют контракт с четырьмя портами (грузопоглощающие точки), но в связи с отдаленностью некоторых объектов поставки являются невыгодными, в связи с этим прочерк между пунктами A2 и B2 ,A3 иB4 означают, что перевозки между указанными пунктами запрещены(Таблица 9).

Таблица 9

Грузопоглощающие точки (Bj) Грузообразующие точки (Ai)
	250	100	150	50
80	6	6	1	4
320	12	-	6	5
150	5	4	3	-

Решение. Проверяем условие баланса:

80+320+150=550=250+100+150 +50.

Для решения задачи полагаем, что стоимости перевозки единицы груза по запрещенным маршрутам равны достаточно большому числу М>0.

Далее эта М-задача решается обычным методом потенциалов, но потенциалы будут зависеть от коэффициента М. Если оптимальный план М-задачи содержит положительные перевозки по запрещенным маршрутам, то исходная ТЗ неразрешима (множество ее планов пусто). В противном случае получаем решение исходной ТЗ.

Предварительный этап. Составляем методом ‘‘минимального

элемента’’ исходный опорный план x₀ (Таблица 10)

Итерация 1. Вычисляем потенциалы и проверяем план на оптимальность

Таблица 10

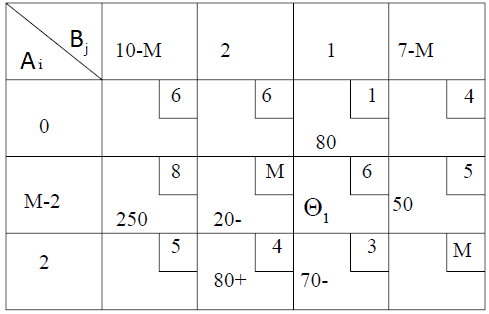
В клетке (2;3) имеем

А2 + В3 = M − 2 + 1 > 6 , т.е. план x₀ не является оптимальным. Проставляем в эту клеткуΘ₁ и составляем замкнутый маршрут. Получаем Θ₁ = 20 . Опорный план x₁ (Таблица 11)

Итерация 2. Проверяем план x₁ на оптимальность:

Таблица 11

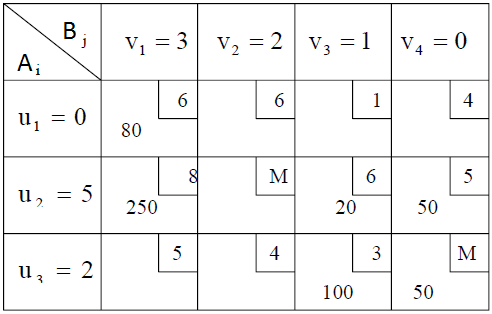
Так как для всех свободных клеток:

A_i +B_j ≤ C_ij,то план x₁ - оптимальный и не содержит положительных перевозок по запрещенным маршрутам.

Минимальные транспортные расходы составляют 3000.

Заключение

В данной работе рассмотрена не только простейшая транспортная задача, но и методы решения транспортной задачи с дополнительными ограничениями, что наиболее приближено к реальным ситуациям определения плана снабжения, в котором суммарные производственные потребности на период планирования сбалансированы с фондами, предназначенными на тот же период. Баланс производства и потребления - необходимое условие составления планов материально-технического снабжения. В рамках же сбалансированности производства и потребления роль системы материально-технического обеспечения заключается в оказании услуг на всех уровнях управления обращением средств производства, которые состоят в размещении заказов на отгрузку конкретных видов продукции по поставщикам, прикреплении потребителей на прямые длительные связи, транзитное и складское снабжение, в установлении оптимальных уровней запасов и методов управления ими, оказании услуг по гарантированному комплексному снабжению, плановому распределению средств производства путем оптовой торговли.

Рациональное прикрепление потребителей к поставщикам в значительной степени определяет структуру хозяйственных связей, их экономическую эффективность. Под оптимальным мы понимаем такой план их прикрепления, который позволяет при минимальных издержках на поставки и содержание запасов максимально использовать производственные мощности поставщиков и бесперебойно питать потребителей.

Именно благодаря методам приведенным в курсовой работе решаются такие задачи, потому что в реальной жизни всегда присутствуют какие либо ограничения.

Список литературы

1. Карманов, В.Г. Математическое программирование: Учебник для вузов. - М.: Наука, 1975. – 260 с.

2. И.Н. Мастяева, О.Н. Семенихина. МЕТОДЫ ОПТИМИЗАЦИИ: /

Московский государственный университет экономики, статистики и

информатики. – М.: МЭСИ, 2003. – 135 с.

3. Ельдештейн Ю.М. ЛОГИСТИКА электронный учебно-методический комплекс

4. В. М. Тропина Методы линейного программирования для решения транспортных задач: Учебное пособие; Тул. гос. ун-т.: Тула, 1999-356 с.