7. Проводники в электростатическом поле. Напряженность поля внутри и вне проводника. Электроемкость проводника (рассмотреть проводник шарообразной формы)

Носители заряда в проводнике способны перемещаться под действием сколь угодно малой силы. Поэтому для равновесия зарядов на проводнике необходимо выполнение следующих условий:

1. напряженность поля всюду внутри проводника должна быть равна нулю 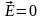; (потенциал внутри проводника должен быть постоянным)

напряженность поля на поверхности проводника должна быть в каждой точке направлена по нормали к поверхности .. Следовательно в случае равновесия зарядов поверхность проводника будет эквипотенциальной. Если проводящему телу сообщить заряд q, то он распределиться так, чтобы соблюдались условия равновесия. Пусть имеет произвольную замкнутую поверхность полностью заключенную внутри тела. При равновесии зарядов поле в каждой точке отсутствует, поэтому поток электрического смещения равен нулю

По теореме Гаусса сумма зарядов внутри поверхности тоже будет равна нулю. Следовательно при равновесии зарядов ни в каком месте проводника не может быть избытка зарядов, они распределяются равномерно по поверхности с некоторой плотностью σ.

Избыточный заряд распределяется на полом проводнике также как и на сплошном – на наружной поверхности. При внесении незаряженного проводника в электрическое поле носители заряда приходят в движение: положительные в направлении вектора , отрицательные в противоположную сторону. В результате на концах проводника возникают заряды противоположных знаков, называемые индуцированными зарядами. Поле этих зарядов направлено противоположно внешнему полю. Перераспределение зарядов происходит до тех пор, пока поле внутри проводника не станет равным нулю, а линии напряженности вне проводника – перпендикулярными к его поверхности. Т. о. нейтральный проводник, внесенный в электрическое поле, разрывает часть линий напряженности – они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются во внешней поверхности проводника. Если внутри проводника имеется полость, то при равновесном распределении зарядов поле внутри проводника становится равным нулю . На этом основывается электростатическая защита. Когда какой-то прибор хотят защитить от воздействия внешнего поля, его окружают проводящим экраном.

Внешнее поле компенсируется внутри экрана возникающими на его поверхности индуцированными зарядами. Такой экран может быть и не сплошным, а сделанным из густой сетки.

Электороемкость. Пусть имеем уединенный проводник, тогда его потенциал пропорционален находящемуся на нем заряду. Действительно увеличение увеличение в несколько раз заряда приводит к увеличению в то же число раз напряженности поля в каждой точке окружающего проводник пространства. Соответственно в такое же число раз возрастает и работа переноса единичного заряда из бесконечности на поверхность проводника, т.е. потенциал проводника. Т.о. для уединенного проводника .

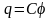Коэффициент пропорциональности С называется электроемкостью проводника (или емкостью) 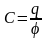. Емкость величина численно равная заряду, сообщение которого изменяет потенциал проводника на единицу. Е диница емкости – Фарада (Ф) 1Ф = 1Кл/1В (Вольт).

Вычислим емкость уединенного шара.

Сначала вычислим потенциал уединенного шара радиусом R. Между разностью потенциалов и напряженностью поля существует связь, поэтому потенциал можно найти проинтегрировав выражение для напряженности поля вне сферы 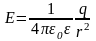по r от R до бесконечности ( ) (потенциал на бесконечности полагаем равным нулю) 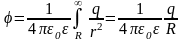. Подставим в формулу для емкости и получим . Емкостью 1Ф обладает уединенный шар радиуса 9*10⁹м, т.е. радиуса в 1500 раз больше радиуса Земли. Следовательно, фарад очень большая величина и на практике используются более мелкие единицы миллифарадом (мФ), микро фарфдом (мкФ), пикофарадом (пФ).