Введение

Совершенствование управления на базе автоматизации ведет к поиску эффективных форм обработки экономической информации и использования ее для принятия управленческих решений.

Лабораторные работы по курсу „Экономико-математические модели в управлении и экономике” предназначены для закрепления теоретического и практического материала, приобретения навыков работы с пакетами прикладных программ, которые обеспечивают построение и исследование различных типов моделей, а также расширение знаний студентов в области применения ПК для экономических расчетов, прогнозирования и анализа деятельности экономических систем.

Для выполнения лабораторных работ предлагается использование программного обеспечения MS EXCEL. Пакет включает статистические методы, которые поддерживают решение разнообразных экономико-математических задач.

Лабораторные работы базируются на основных темах дисциплины и обосновываются на теоретическом материале соответствующей темы и предыдущих темах. Каждая работа содержит цель, задания и методические указания для выполнения, а также варианты задачи.

Для сдачи лабораторной работы студенту необходимо оформить индивидуальный отчет, который включает: постановку задачи, распечатки основных результатов построения модели, анализ расчетов и выводы.

Оценка за выполнение работы ставится по результатам выполнения и защиты лабораторной работы. Внимание уделяется знанию теоретического материала, правильности выводов и полноте экономической интерпретации полученных результатов.

В подготовке лабораторных работ использовались научные методики построения экономико-математических моделей деятельности предприятий в современных условиях.

Лабораторная работа № 1 реализация детерминированной модели деятельности предприятия с помощью электронной таблицы ms excel

Цель – приобрести навыки моделирования электронных таблиц для создания отчета о финансово-экономической деятельности производственного предприятия с целью получить прибыль.

Модель бизнес-ситуации. Постановка задачи

Вновь созданная фирма „Вкусная еда” специализируется на том, что делает из двух закупаемых компонентов (фруктов и замороженного теста) яблочные пироги, обрабатывает их (выпекает, упаковывает, доставляет) и продает местным бакалейным магазинам.

Ставятся задачи:

- построить модель в электронной таблице Excel;

- выполнить анализ чувствительности модели;

- исследовать модель с помощью деловой графики;

- изучить возможности дальнейшего расширения фирмы.

Порядок выполнения работы

1. На основе теоретических знаний построить детерминированную модель в виде „черного ящика” и диаграмму влияния. Определить следующие переменные входа:

- цена пирога;

- спрос и объем продаж в неделю;

- удельные (на один пирог) затраты на обработку;

- удельные затраты на закупку начинки;

- удельные затраты на закупку теста;

- постоянные недельные издержки.

Математические уравнения для получения прибыли:

Прибыль = Доход – Общие затраты,

Доход = Цена пирога Спрос,

Общие затраты = Затраты на обработку + Затраты на продукты + Постоянные издержки,

Затраты на продукты = Количество начинки Удельные затраты на начинку + Количество теста Удельные затраты на тесто.

При построении моделей в электронных таблицах рекомендуется:

1. Переменные входа представлять вместе в виде отдельной поименованной таблицы.

2. Четко обозначить выходные результаты модели.

3. Там, где нужно, указывать единицы измерения.

4. Параметры хранить в отдельных ячейках и вызывать в формулах с использованием адресации ячеек.

5. Для удобства чтения таблиц следует использовать полужирный шрифт, сдвиг содержимого ячеек, подчеркивание и другие предлагаемые Excel возможности форматирования.

2. Построить на первом листе (Лист1) рабочей книги таблицу „Модель недельной прибыли” (рис. 1.1).

Рис. 1.1. Модель получения недельной прибыли в электронной таблице в числовом виде и с использованием формул

3. Скопировать построенную модель на Лист2 и провести анализ модели при изменении ее параметров (анализ „что-если…”):

- увеличить спрос на 4000 штук при уменьшении цены на 1 гр за штуку;

- уменьшить спрос на 4000 штук при увеличении цены на 1 гр за штуку.

Сделать выводы об изменении прибыли.

4. Уточнить модель, установив обратно пропорциональную зависимость между ценой пирога и спросом (чем выше цена, тем меньше спрос или продажи).

На листе 2 скопировать содержимое диапазона В2:В19 в столбцы С, D, E, F, G, H. Ввести цену пирога от 6 гр. до 12 гр, а спрос – от 24 000 штук до 0 штук. Соотношение исходных данных цены (в примере – 8 гр. за штуку) и спроса (в примере – 16 000 штук) за неделю должно быть зафиксировано в одном из столбцов.

Построить точечную диаграмму зависимости спроса от цены пирога. Добавить линию тренда и обеспечить вывод его уравнения.

Должна получиться зависимость:

Спрос = a Цена пирога + b.

В примере a = -4 000 и b = 48 000. На рис. 1.2 показаны результаты анализа модели для ее уточнения.

Рис. 1.2. Результаты анализа модели

На следующем листе Лист3 сформировать уточненную модель, в которой входная переменная Спрос является линейной функцией переменной Цена (рис.1.3), т.е. внести в ячейку В10 полученное значение b, а в ячейку В11 – a.

Рис. 1.3. Модель производства, в которой отражена связь между спросом и ценой пирога

Для анализа „что-если…” на листе 4 скопировать содержимое диапазона В2:В21 в столбцы С, D, E, F, G, H. Ввести цену пирога от 6 гр. до 12 гр.

Построить точечные диаграммы зависимости финансовых результатов от цены пирога. Пример результата показан на рис. 1.4.

Рис. 1.4. Выходные результаты для различных значений цены

Сделать выводы по графическому анализу модели, выбрать оптимальную цену пирога. В данном примере определено, что прибыль будет наибольшей при значении цены около 9,00 гр, а точка безубыточности, в которой прибыль становится равной 0, соответствует цене, приблизительно равной 6,25 гр. Кроме того, из графика следует, что прибыль не слишком зависит от цены около 9,00 гр.

5. Скопировать исходную модель на новый лист рабочей книги и выполнить анализ чувствительности модели. В ходе анализа чувствительности исследуется воздействие (относительно незначительных) изменений входных переменных на другие переменные, чаще всего — на показатель эффективности.

С этой целью выбрать базовое значение цены, при которой прибыль максимальная (в примере 9,00 гр). Исследовать воздействие малых изменений цены на прибыль, которая является критерием эффективности.

Использовать экономический подход – анализ эластичности: на сколько процентов изменится прибыль при заданном процентном изменении цены. Включить в модель дополнительные строки для вычисления процентных отношений. На рис. 1.5. показан пример проведенных расчетов.

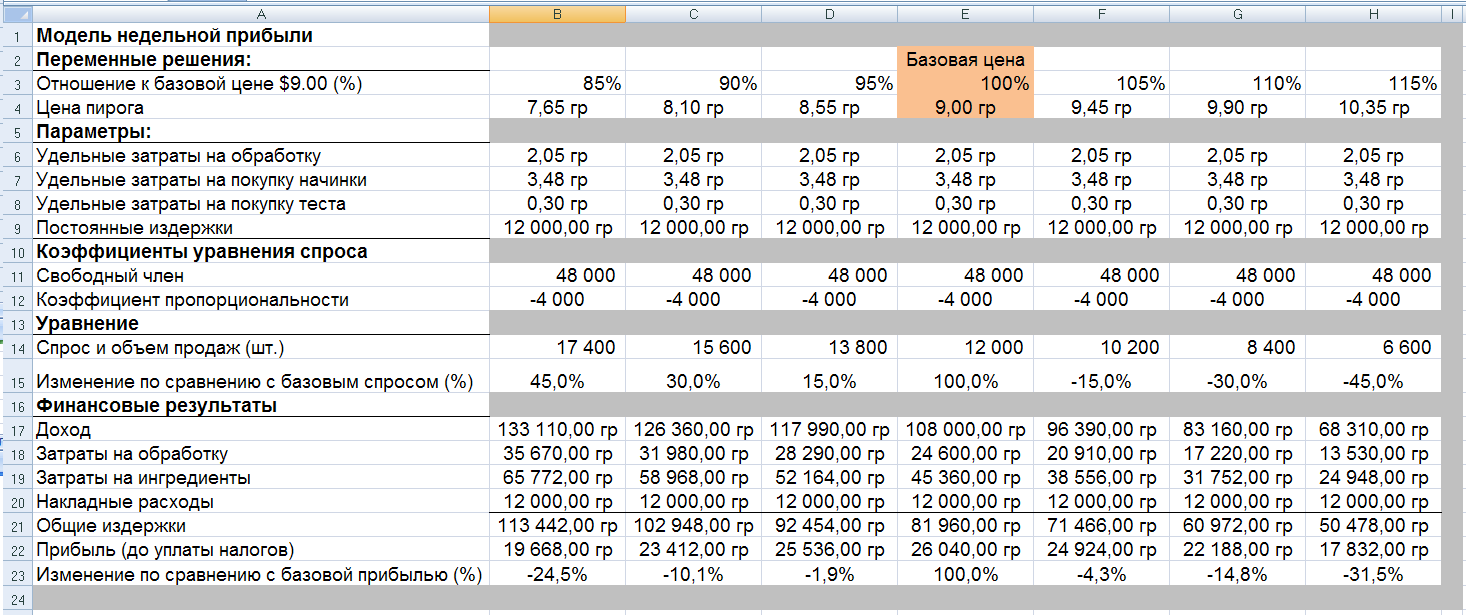
Рис. 1.5. Анализ чувствительности модели

Сделать выводы о влиянии цены на прибыль. В примере анализ чувствительности (рис. 1.5) открыл важный факт: небольшое (5%) уменьшение цены по сравнению с базовой приводит к заметному росту спроса и продаж (15%) при совсем незначительном снижении недельной прибыли (менее 2%). Можно установить цену 8,10 гр, что на 10% ниже базовой, но тем самым потерять около 10% прибыли, чтобы добиться 30% увеличения недельного объема продаж. Это решение привлекательно, так как компания имеет статус вновь созданной, и ей нужно быстро завоевывать рынок и привлечь клиентов. Такие соображения часто называют анализом компромиссов, поскольку они отражают, насколько нужно пожертвовать одним критерием эффективности (прибылью), чтобы добиться определенного улучшения другого критерия (спрос и объем продаж).

6. На новом листе сформировать модель прибыли за месяц. Указать различные цены для каждой недели. В столбце „Итого” найти суммы результатов модели. Пример формирования модели прибыли за месяц показан на рис. 1.6.

Рис. 1.6. Модель производства за месяц

7. Выполнить табличные и графические исследования зависимости результатов модели от цены. Использовать инструмент Excel – Таблица подстановки (Таблица данных для MS Excel-2007).

Таблица подстановки с одним входом позволяет изменять только одну входную переменную, но при этом рассчитывает значения нескольких выходных переменных.

Задать в строке значения переменной оптимальные цены яблочного пирога с разницей в 0,1 – 0,2 гр. Сформировать два столбца с выходными данными модели: 1) названия переменных – спрос, доход, общие издержки и прибыль; 2) ссылки на ячейки рабочего листа, содержащие формулы для вычисления значений этих переменных. Общий вид таблицы подстановки с одним входом и соответствующими формулами показан на рис. 1.7.

Рис. 1.7. Структура таблицы подстановки с одним входом для модели

После выделения диапазона ячеек F2:P6, содержащего все строки таблицы и левый столбец со ссылками на ячейки модели, выбирается команда Таблица подстановки… (Таблица данных…). Поскольку значения переменной задаются в первой строке, ссылка на ячейку рабочего листа, указывающая, куда нужно подставлять эти значения, задается в поле Подставлять значения по столбцам в диалогового окна Таблица подстановки, как показано на рис. 1.8. Второе поле ввода в диалоговом окне Таблица подстановки остается пустым.

Рис. 1.8. Создание таблицы подстановки с одним входом

После нажатия на кнопку ОК в диалоговом окне Таблица подстановки рабочий лист будет пересчитан для каждого значения переменной.

Построить по полученной таблице точечные диаграммы зависимости результатов модели от цены. Пример заполнения таблицы и диаграммы представлен на рис. 1.9.

Рис. 1.9. Таблица подстановки с одним входом и диаграмма для модели производства пирогов

Сделать выводы о дальнейшем расширении фирмы: недогруженность производственной мощности фирмы, возможность выпуска пирогов с другой начинкой, исследование затрат (создание математических моделей для вычисления затрат и др.).

Сохранить файл.

Варианты значений входных параметров

Вари-ант	Цена пирога в гр	Спрос и объем продаж в шт.	Удельные затраты на производство в гр	Удельные затраты на закупку начинки в гр	Удельные затраты на закупку теста в гр	Постоянные недельные издержки в гр
1	8,50	16 000	2	3,48	0,30	12 000
2	8,50	16 500	2,01	3,48	0,30	12 500
3	8,50	16 000	2,02	3,48	0,30	13 000
4	8,50	16 500	2,03	3,48	0,30	12 000
5	8,50	16 000	2,04	3,48	0,30	12 500
6	8,50	16 500	2,05	3,48	0,30	13 000
7	8,50	16 000	2,06	3,48	0,30	12 000
8	8,50	16 500	2,07	3,48	0,30	12 500
9	8,50	16 000	2,08	3,48	0,30	13 000
10	8,50	16 500	2	3,48	0,30	12 000
11	8	16 000	2,01	3,48	0,30	12 500
12	8	16 500	2,02	3,48	0,30	13 000
13	8	16 000	2,03	3,48	0,30	12 000
14	8	16 500	2,04	3,48	0,30	12 500
15	8	16 000	2,05	3,48	0,30	13 000
16	8	16 500	2,06	3,48	0,30	12 000
17	8	16 000	2,07	3,48	0,30	12 500
18	8	16 500	2,08	3,48	0,30	13 000
19	8	16 000	2,09	3,48	0,30	12 000
20	8	16 500	2	3,48	0,30	12 500
21	9	16 000	2,01	3,48	0,30	13 000
22	9	16 500	2,02	3,48	0,30	12 000
23	9	16 000	2,03	3,48	0,30	12 500
24	9	16 500	2,04	3,48	0,30	13 000
25	9	16 000	2,05	3,48	0,30	12 000
26	9	16 500	2,06	3,48	0,30	12 500
27	9	16 000	2,07	3,48	0,30	13 000
28	9	16 500	2,08	3,48	0,30	12 000
29	9	16 000	2,09	3,48	0,30	12 500
30	9	16 500	2	3,48	0,30	13 000