Числовые характеристики случайных величин.
Одно из центральных понятий теории вероятностей - понятие случайной величины.
Случайная величина - это величина, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Математическое ожидание. Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений хi с вероятностями рi , называется сумма:
(6а)
Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f(x):
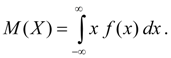(6б)
Несобственный интеграл (6б) предполагается абсолютно сходящимся (в противном случае говорят, что математическое ожидание М ( Х ) не существует). Математическое ожидание характеризует среднее значение случайной величины Х. Его размерность совпадает с размерностью случайной величины.
Дисперсия. Дисперсией случайной величины Х называется число:
(6в)
Дисперсия
является характеристикой рассеяния
значений случайной величины Х относительно
ее среднего значения М ( Х ). Размерность
дисперсии равна размерности случайной
величины в квадрате. Исходя из определений
дисперсии (8) и математического ожидания
(5) для дискретной случайной величины и
(6) для непрерывной случайной величины
получим аналогичные выражения для
дисперсии:
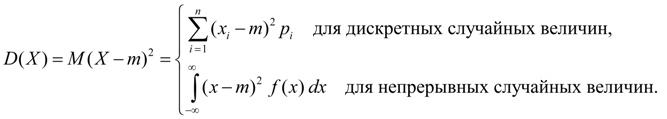
где m = М ( Х ).
Среднее квадратичное отклонение:
(6г)
Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.