4. Формула полной вероятности и формулы Бейеса

Формула полной вероятности применяется в тех случаях, когда при выполнении события В имеется несколько вариантов его осуществления. Каждый вариант связан с определенной гипотезой. Гипотезы представляют собой множество попарно несовместных событий. Событие В обязательно выполняется, причем, только с одной из гипотез, но с какой именно – неизвестно.

Рассмотрим полную группу n попарно несовместимых событий А₁, А₂, ... А_n, то есть U = А₁+А₂+...+А_n и А_iА_j=V при 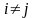, и некоторое событие В. Возьмем произведение события U на событие В:

и, применяя свойства операций над событиями, получим

.

События А_iB и А_j B при i ≠ j попарно несовместимы, так как . По теореме сложения вероятностей для несовместимых событий получим

,

далее, применяя теорему умножения, окончательно будем иметь

. (4.1)

Итак, вероятность Р(В) события В, которое может произойти только совместно с одним из событий А₁, А₂, ... А_n, образующих полную группу попарно несовместимых событий, определяется последней формулой, носящий название формулы полной вероятности.

Пример 1. Имеется 5 одинаковых на вид урн. Из них в двух урнах находятся по 3 белых и 1 черному шару (урна I типа), а в трех урнах – по 3 черных и 1 белому шару (урна II типа). Наугад выбирают одну из урн и из нее наугад извлекают шар. Найти вероятность того, что он окажется белым.

Решение. Имеет две гипотезы: А₁ – шар извлечен из урны I типа,

А₂ – шар извлечен из урны II типа.

Вероятность того, что будет выбрана урна первого типа, равна Р (А₁) =2/5, а для урн второго типа эта вероятность равна Р (А₂) =3/5. Вероятность того, что из урны первого типа будет извлечен белый шар, равна =3/4, соответствующая вероятность для урн второго типа равна 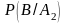=1/4. Пользуясь формулой полной вероятности, получаем вероятность того, что шар, выбранный наугад, окажется белым, равна .

Пусть, как и при выводе формулы полной вероятности, событие В может наступить в различных условиях, относительно которых можно сделать n предположений, гипотез: А₁, А₂, ... А_n. Вероятности Р(А₁), Р(А₂),..., Р(А_n) этих гипотез известны до испытания, и, кроме того, известна вероятность P(B/A_i), сообщаемая событию В гипотезой А_i. Пусть после проведенного испытания событие В наступило, требуется при этом условии найти вероятность гипотезы.

Воспользуемся для вывода формулы искомой вероятности теоремой умножения:

,

Откуда .

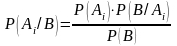Подставив в знаменатель этой формулы правую часть формулы полной вероятности (4.1), окончательно будем иметь:

. (4.2)

Полученные формулы носят название формул вероятности гипотез, или формул Бейеса.

Пример 2. Предположим, что в условии примера 1 извлеченный шар оказался белым. Найти вероятность того, что он оказался извлеченным из урны первого типа.

Решение. Применяя формулу (4.2), получаем

.

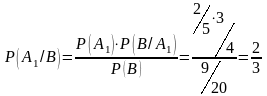5. Повторение испытаний

5.1 Формула Бернулли

При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание (опыт) повторяется многократно.

Поставим задачу в общем виде. Пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие . Проведем n испытаний Бернулли. Это означает, что все п испытаний независимы; вероятность появления события А в каждом отдельно взятом испытании постоянна и от испытания к испытанию не изменяется (то есть испытания проводятся в одинаковых условиях). Обозначим вероятность Р(А) появления события в единичном испытании буквой p, то есть Р(А)=р, а вероятность Р( ) – буквой q, то есть .

Вероятность Р_n(m) наступления события A ровно m раз (не наступления события n-m раз) в этих n испытаниях, при условии, что здесь не требуется появление т раз события А в определенной последовательности, вычисляется по формуле

, (5.1)

которую называют формулой Бернулли.

Пример 1. Монету бросают наугад 5 раз. Найти вероятность того, что герб выпадет при этом 3 раза.

Решение. , тогда по формуле Бернулли (5.1) получаем .