Функциональные последовательности и ряды

1. Основные определения

Пусть M – некоторое числовое множество

Если каждому натуральному числу n поставлена в соответствие некоторая функция определенная на множестве M, то говорят, что на множестве M задана функциональная последовательность

. (1)

П

ри каждом фиксированном функциональная последовательность (1) превращается в числовую .

 , .

.

.

Пусть на множестве M определена функциональная последовательность и при функциональная последовательность (1) превращается в сходящуюся числовую последовательность . Тогда говорят, что функциональная последовательность (1) сходится в точке .

 Функциональная последовательность сходится в точках

, ,

, ,

.

Если функциональная последовательность сходится в каждой точке множества M, говорят, что она сходится на множестве M.

 Функциональная последовательность сходится на множестве

Пусть функциональная последовательность (1) сходится на множестве M и функция, которая на множестве M определяется формулой

, (2)

тогда называется предельной функцией функциональной последовательности (1) на множестве M.



Найдем предельную функцию

функциональной последовательности

, , .

При ,

При ,

При .

Таким образом, предельная функция имеет вид .

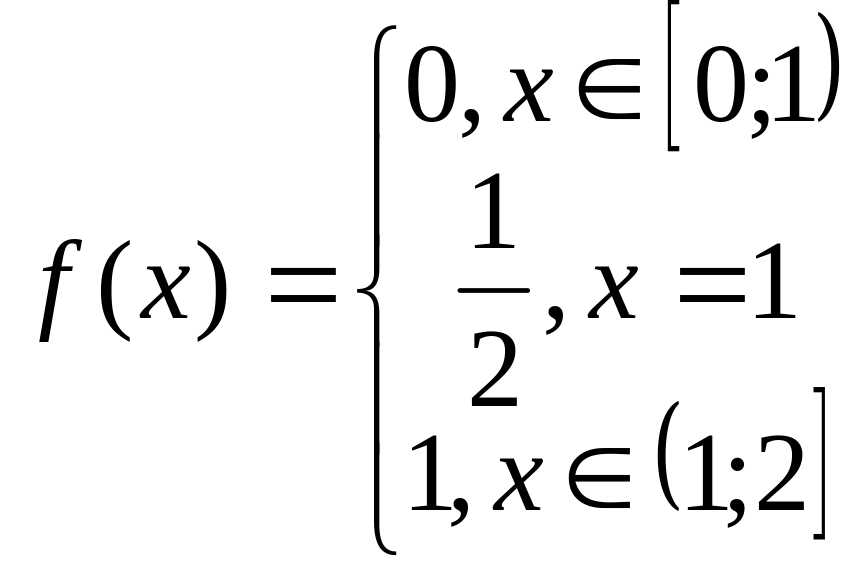Пусть на множестве M определена функциональная последовательность , тогда выражение

или

(3)

называется функциональным рядом на множестве M (функциональный ряд).

При каждом фиксированном функциональный ряд (3) превращается в числовой ряд.

Пусть на множестве M задан функциональный ряд тогда функции

(4)

называются частичными суммами функционального ряда.

Говорят, что функциональный ряд (3), заданный на множестве M сходится или расходится в точке , если в этой точке сходится или расходится функциональная последовательность частичных сумм функционального ряда, т.е. сходится или расходится числовой ряд .

Пусть функциональный ряд (3) сходится на числовом множестве M и - предельная функция функциональной последовательности частичных сумм функционального ряда (4), тогда эту функцию называем суммой данного функционального ряда и пишут

. (5)

Очевидно, при каждом является обычной суммой числового ряда .

2. Равномерная сходимость функциональных последовательностей

Пусть функциональная последовательность (1) сходится на числовом множестве M к предельной функции . Это означает, что

, такое, что при всех будет .

Обратим внимание на то, что N зависит не только от , но и от точки .

Если номер оказывается пригодным сразу для всех значений и зависит только от . В этом случае функциональную последовательность (1) называют равномерно сходящейся на множестве M.

Пусть на числовом множестве задана функциональная последовательность (1). Говорят, что эта последовательность сходится на множестве M равномерно к функции , если выполняется:

, такое, что при всех и будет . (6)

Th1. Критерий Коши равномерной сходимости функциональной последовательности

Для того, чтобы функциональная последовательность (1) равномерно сходилась на часловом множестве M необходимо и достаточно, чтобы

, такое, что при всех , и будет . (7)

□

Необходимость. Предположим, что функциональная последовательность сходится равномерно на множестве M. Обозначим - предельную функцию этой функциональной последовательности. Возьмем произвольное и , для этого будет выполняться условие (6), тогда

.

Доказано (7).

Достаточность. Предположим, что числовое условие (7) выполняется в некоторой точке , тогда числовая последовательность сходится к предельной функции .

Докажем теперь равномерную сходимость.

Возьмем произвольно и положим . Обозначим через такое натуральное число, что при всех и и для будет выполняться (7). Так как и , тогда выполняется одновременно и .

Тогда

, что означает равномерную сходимость (1).

■

Th2. Второй критерий

Для того, чтобы функциональная последовательность (1) равномерно сходилась к предельной функции на множестве M необходимо и достаточно, чтобы

(8)

□

Необходимость. Пусть выполняется условие (6), покажем, что тогда выполняется (8).

Возьмем произвольное. По нему найдем N из выполнения условия (6).

Если теперь , то для всех , тогда . В силу произвольности это означает выполнение (8).

Достаточность. Пусть выполняется условие (8). Возьмем - произвольное, тогда для этого найдем N из выполнения условия (8): т.е. такое, что для выполняется , тогда, тем более , то есть выполняется условие равномерной сходимости функциональной последовательности (6).

■



Исследуем функциональную последовательность на равномерную сходимость , , .

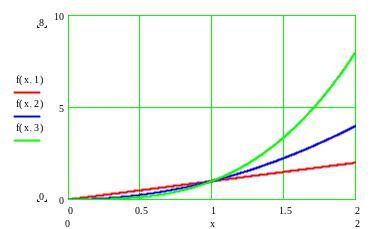
1. Найдем предельную функцию .

, следовательно .

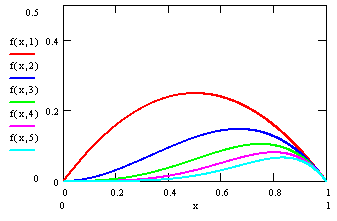
2. Найдем Исследуем на max, функцию , производная - точка max, , , - максимальное значение функции.

3. Найдем =

=0.

Ответ: исходная функциональная последовательность сходится к равномерно.