
- •1. Структурная схема системы цифровой связи
- •Исходные данные.
- •Расчет характеристик источника сообщения:
- •Аналого-цифровой преобразователь
- •Построение решетчатой диаграммы кодера
- •Формирователь модулирующих сигналов
- •Модулятор
- •Написать аналитические выражения для корреляционной функции сигнала и для спектральной плотности мощности сигнала заданного вида квадратурной модуляции на выходе сумматора.
- •Декодер
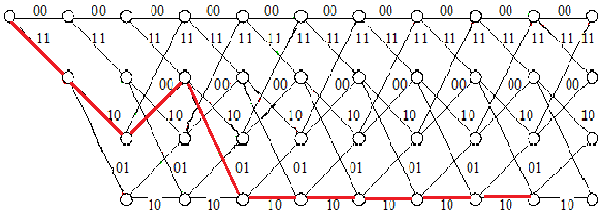
Построение решетчатой диаграммы кодера
Обозначим буквами a, b, c, d состояния сверточного кодера: a = 00,b = 10, c = 01, d = 11. При построении решетчатой диаграммы поступление на вход кодера символа «0» отмечается сплошной линией, а символа «1» - пунктирной. Над каждой линией (ребром) указаны символы, формируемые на выходе кодера. Последовательность информационных символов, поступающих на вход сверточного кодера заканчивается и в ее конце передают K - 1 нулей (так называемый хвост кода). В результате кодер переходит в состояние a. После этого он готов к приему следующей информационной последовательности
-
Информационные
символы (ИС)
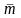
1
0
1
1
1
1
1
1
1
Кодовые символы (КС)

11
10
00
01
10
10
10
10
10
При b(iT) = 101111111 c(iTb) = 111000011010101010
Определить длительность двоичного символа ТВ на выходе кодера (в последовательном формате)

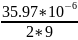 =2
мкс.
=2
мкс.
Определить техническую скорость передачи VВ
VВ
=
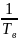 =
=
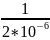 = 500000 символов/с
= 500000 символов/с
Формирователь модулирующих сигналов
С
выхода кодера (К) формируются реализации
случайного сигнала (процесса)
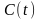 и поступают на вход блока ФМС. В сигнал
с выхода сверточного кодера представляет
собой случайную последовательность
однополярных прямоугольных импульсов
с амплитудой
и поступают на вход блока ФМС. В сигнал
с выхода сверточного кодера представляет
собой случайную последовательность
однополярных прямоугольных импульсов
с амплитудой
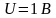 .
Предполагается, что этот сигнал
преобразуется в последовательность
биполярных прямоугольных импульсов:
.
Предполагается, что этот сигнал
преобразуется в последовательность
биполярных прямоугольных импульсов:
-
символ «1» передается импульсом
положительной полярности с амплитудой
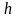 [9, с. 148]) и длительностью
[9, с. 148]) и длительностью
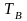 ,
где
бинарный интервал;
,
где
бинарный интервал;
-
символ «0» передается импульсом
отрицательной полярности. Параметр
безразмерная величина и может
принимать любые заданные значения,
например
 .
.
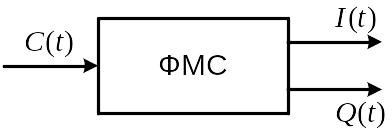
Формирователь модулирующих символов (ФМС).
Блок ФМС имеет два выхода, на которых формируются выходные
сигналы
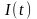 и
и
 .
.
Реализацию
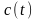 случайного процесса
случайного процесса
 (30)
(30)
можно представить в следующей аналитической форме
 (31),
(31),
где
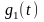 прямоугольный импульс длительностью
(рис. 13,а),
прямоугольный импульс длительностью
(рис. 13,а),
 при
при
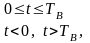 (32).
(32).
где
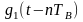 прямоугольный импульс такой же
формы, как
,
но сдвинутый вправо относительно
импульса
на величину
прямоугольный импульс такой же
формы, как
,
но сдвинутый вправо относительно
импульса
на величину
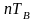 ,
если
,
если
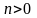 ,
или влево, если
,
или влево, если
 ;
;
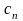 - численный коэффициент, являющийся
реализацией случайной величины
- численный коэффициент, являющийся
реализацией случайной величины
 на
на
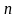 - интервале
.
- интервале
.
Величина
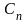 принимает два дискретных значения
и
принимает два дискретных значения
и
 с вероятностью 0,5 каждое, т. е.
с вероятностью 0,5 каждое, т. е.
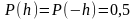 .
.
Если
в заданной реализации
на
интервале передается информационный
символ «1», то
 ,
если передается символ «0», то
,
если передается символ «0», то
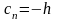 .Связь
между входным сигналом и выходными
сигналами блока ФМС характеризует
сигнальное созвездие для заданного
вида модуляции. Сигнальное созвездие
строится в декартовой системе координат
.Связь
между входным сигналом и выходными
сигналами блока ФМС характеризует
сигнальное созвездие для заданного
вида модуляции. Сигнальное созвездие
строится в декартовой системе координат
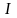 и
и
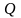 .
Каждой точке (звезде) сигнального
созвездия будут соответствовать
численные значения координат
и
.
Существуют разные формы сигнальных
созвездий, но наибольшее практическое
применение получили созвездия квадратной
формы. Примерами таких созвездий являются
КАМ-16
.
Каждой точке (звезде) сигнального
созвездия будут соответствовать
численные значения координат
и
.
Существуют разные формы сигнальных
созвездий, но наибольшее практическое
применение получили созвездия квадратной
формы. Примерами таких созвездий являются
КАМ-16
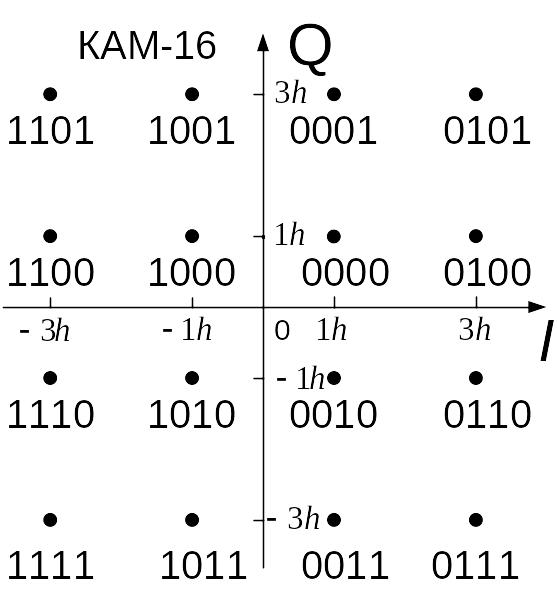
Число точек в
созвездии равное 16 представляем в виде
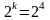 ,
где
,
где
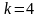 .
Определяем величину
.
Определяем величину
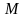 – число дискретных значений, которые
могут принимать координаты
и
точек на сигнальном созвездии, т. е.
– число дискретных значений, которые
могут принимать координаты
и
точек на сигнальном созвездии, т. е.
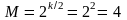 .
Используя , находим значения координат
точек созвездия КАМ-16 на осях
и
:
–3
,
–
,
,
3
.
.
Используя , находим значения координат
точек созвездия КАМ-16 на осях
и
:
–3
,
–
,
,
3
.
Использованием
сигнального созвездия КАМ-16 строятся
реализации
 и
и
 выходных случайных процессов
и
.
Процессы
и
можно представить в виде
выходных случайных процессов
и
.
Процессы
и
можно представить в виде
 ;
;
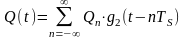 ,
,
где
 – прямоугольный импульс длительностью
– прямоугольный импульс длительностью

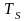 – символьный интервал;
– бинарный интервал.
– символьный интервал;
– бинарный интервал.
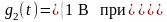

где
 – прямоугольный импульс такой же формы,
как импульс
,
но сдвинутый вправо относительно
импульса
на величину
– прямоугольный импульс такой же формы,
как импульс
,
но сдвинутый вправо относительно
импульса
на величину
 ,
если
,
или влево, если
;
,
если
,
или влево, если
;
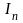 и
и
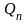 – независимые случайные величины,
заданные на символьном интервале с
номером
,
которые согласно сигнальному созвездию
принимают четыре дискретных значения
– независимые случайные величины,
заданные на символьном интервале с
номером
,
которые согласно сигнальному созвездию
принимают четыре дискретных значения
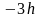 ,
,
,
,
,
,
 с вероятностью 0,25 каждое, т. е.
с вероятностью 0,25 каждое, т. е.

Изобразить график реализации c(t) случайного процесса C(t)
на входе блока ФМС (выходе сверточного кодера) для первых 16 бинарных интервалов

Осциллограмма реализации с выхода сверточного кодера
Написать аналитическое выражение для случайного процесса .
где прямоугольный импульс длительностью
 при
при
где прямоугольный импульс такой же формы, как , но сдвинутый вправо относительно импульса на величину , если , или влево, если ; - случайная величина 0, +h (значение бита на - интервале ).
В соответствии с сигнальным созвездием модулятора QPSK
(или QASK) изобразить для входной реализации графики реализаций и на выходе блока ФМС случайных процессов и .Написать аналитические выражения для случайных процессов и .
;
где прямоугольный импульс длительностью TS.

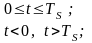 (36)
(36)
прямоугольный импульс такой же формы, как импульс , но сдвинутый вправо относительно импульса на величину , если , или влево, если ; и независимые случайные величины, заданные на символьном интервале с номером , которые согласно сигнальному созвездию принимают:
для QАSK четыре дискретных значения –3h, –h, +h , +3h с вероятностями

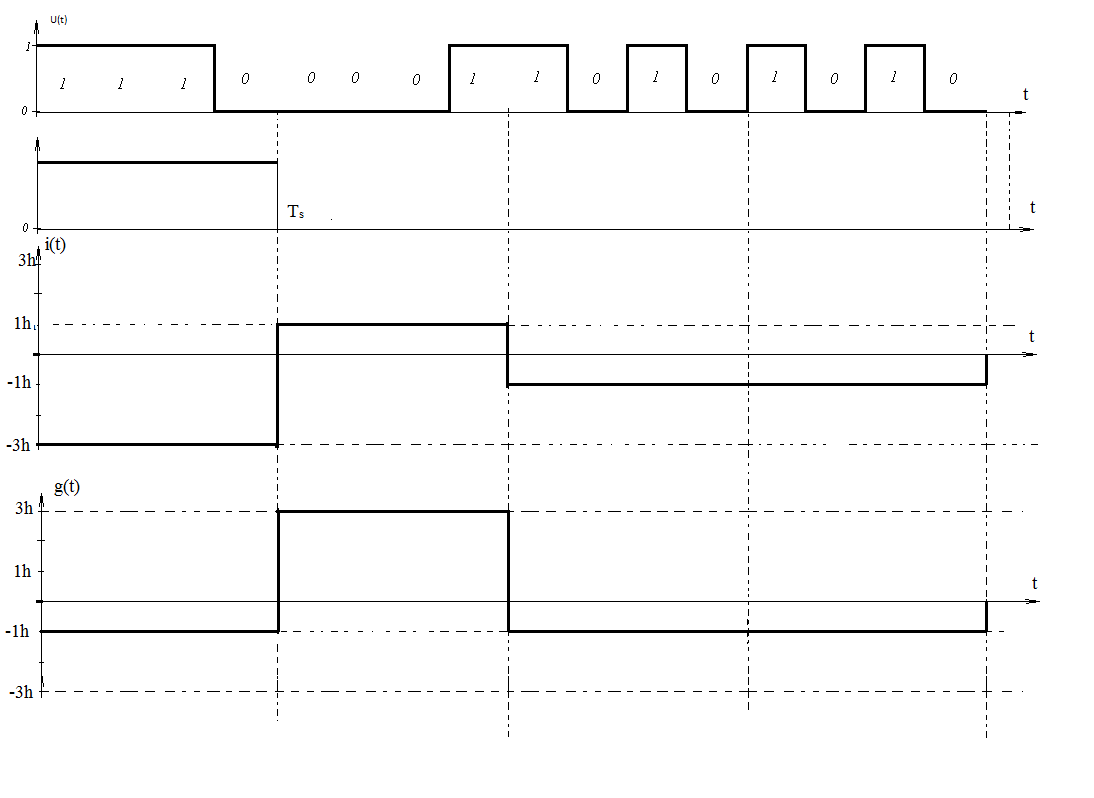
Фрагменты реализаций и случайных процессов и , соответствующие заданной реализации входного процесса .
Написать аналитические выражения для корреляционной функции
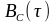 и спектральной плотности мощности
и спектральной плотности мощности
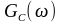 входного случайного процесса
и построить графики этих функций.
входного случайного процесса
и построить графики этих функций.
Процесс C(t) является случайным синхронным телеграфным сигналом. Его корреляционная функция имеет вид
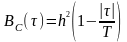 ,
,
а энергетический спектр
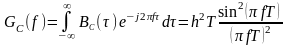 ,
,
где Т = ТВ – длительность тактового интервала.
Графики BC(τ) и GC(f) приведены на рис.
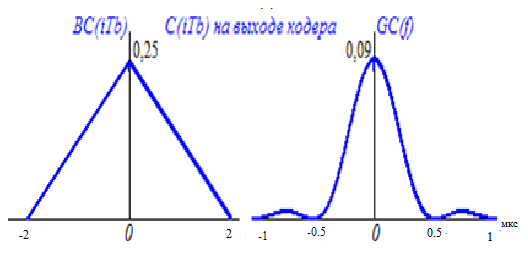
Корреляционная функция BC(τ) (а) и энергетический спектр GC(f) (б)
синхронного телеграфного сигнала C(t)
5. Написать аналитические выражения для корреляционных функций
BI(τ) и BQ(τ), спектральных плотностей мощности GI(f) и GQ(f) случайных процессов I(t) и Q(t). Построить графики этих функций.
Процессы I(t) и Q(t) отличаются от процесса C(t) длительностями тактовых интервалов (TS = 4TB для QАSK), а для QАSK ещё и начальными значениями BI(0) = BQ(0) = D[I(t)] = D[Q(t)] и GI(0) = GQ(0) = D[I(t)]/ TS = D[Q(t)]/ TS

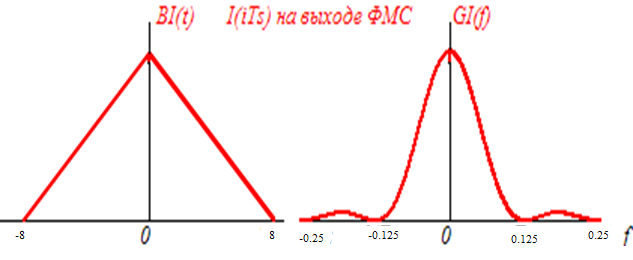
Корреляционная функция BI(τ) (а) и
энергетический GI(f) спектр (б) синхронного телеграфного сигнала I(t)
Если сигнал расширить в 4 раза, то спектр сжимается в 4 раза
7. Определить длительность символьного интервала TS.
TS = 4TB ,
где TB - бинарный интервал). TS = 4TB = 4·2*10-6 = 8 мкс .
