17. Аналіз електричних кіл методом вузлових напруг.

Метод вузлових напруг є найбільш загальним і широко застосовується для розрахунку електричних ланцюгів, зокрема в різних програмах автоматизованого проектування електронних схем.

Струм в будь-якої гілки складного ланцюга можна знайти, визначивши різницю потенціалів між вузлами. Метод розрахунку, заснований на визначенні напружень між вузлами складного ланцюга, називають методом вузлових напруг (вузлових потенціалів).

Число невідомих у цьому методі визначається кількістю рівнянь, які необхідно скласти за першим законом Кірхгофа, тобто метод вузлових напруг теж є модифікацією методу Кірхгофа. Даний метод має переваги у порівнянні з методом контурних струмів, коли кількість вузлів менше числа незалежних контурів складного ланцюга.

Прийнявши потенціал одного з вузлів (базисного або опорного) рівним нулю, одержимо деякі напруження інших вузлів відносно базисного, звані вузловими напругами.

Визначимо струми у всіх гілках ланцюга (рис.1), наведеної в прикладі 1.

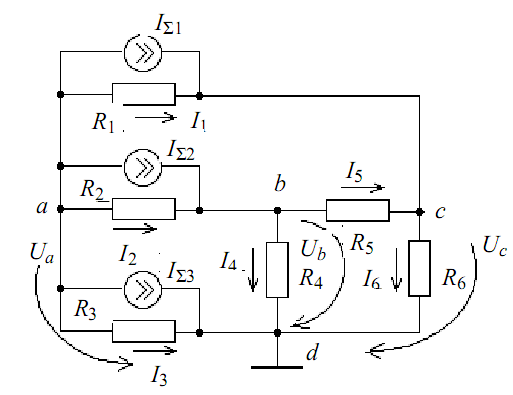
Рис.1.

Для вузлів a, b, c система рівнянь, складених по першому закону Кіргофа, наступна

де - струми джерел струму.

Струми, що протікають через опори,

Підставивши ці значення в останню систему рівнянь, отримаємо:

де .

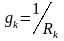Величини, що представляють собою суму провідностей гілок, що сходяться в даному вузлі, називаються власною провідністю вузла, величина, що дорівнює провідності гілки між вузлами, що входить зі знаком мінус у систему рівнянь, називається загальною провідністю між вузлами.

Вирішивши дану систему рівнянь, одержимо вузлові напруги і далі за законом Ома визначимо струми в гілках.

У загальному випадку для складного ланцюга, що містить g вузлів:

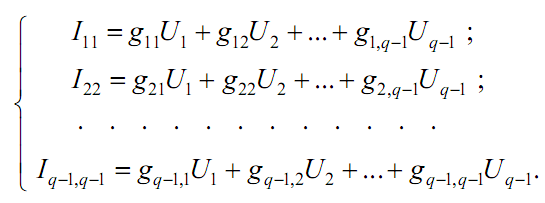
Тут I₁₁, I₂₂ …, I_q-1,q-1 - алгебраїчна сума струмів джерел, пов'язаних з вузлами; g_ii - власна провідність i-го вузла; g_ik - загальна провідність між i-м і k-м вузлами, що входить із знаком (-) при обраному напрямку вузлових напруг до базисного вузла.

Вирішивши систему рівнянь за допомогою визначників, отримаємо:

де Δ – визначник системи

Δ_ik – алгебраічне доповнення елемента g_ik , отримане із визначника Δ шляхом викреслення k-го стовпчика та і-го рядка та множенням отриманого визначника на .

В розгорнутому вигляді:

З останніх рівнянь випливає, що вузлові напруги визначаються алгебраїчною сумою приватних вузлових напруг, обумовлених дією кожного джерела струму, тобто як і в методі контурних струмів, ці рівняння відображають принцип накладення, характерний для лінійних електричних ланцюгів. У рівняннях з'являються додаткові складові, обумовлені взаємної провідністю між вузлами через залежні джерела.

18. Метод комплексних амплітуд розрахунку кіл при гармонічної дії.

При гармонійному впливі на лінійну ланцюг всі струми і напруги мають форму гармонійних коливань, тому завдання розрахунку ланцюга зводиться до знаходження амплітуд і початкових фаз цих коливань. У зв'язку з цим був розроблений метод комплексних амплітуд, заснований на представленні гармонійних функцій у вигляді проекцій обертових векторів, які виражаються аналітично в комплексній формі. Метод зручно поєднує аналітичні розрахунки з геометричними уявленнями.

Гармонійні коливання згідно методу комплексних амплітуд можуть бути представлені як проекції вектора на комплексній площині обертового проти годинникової стрілки з кутовою частотою ω (рис. 1) на осі координат.

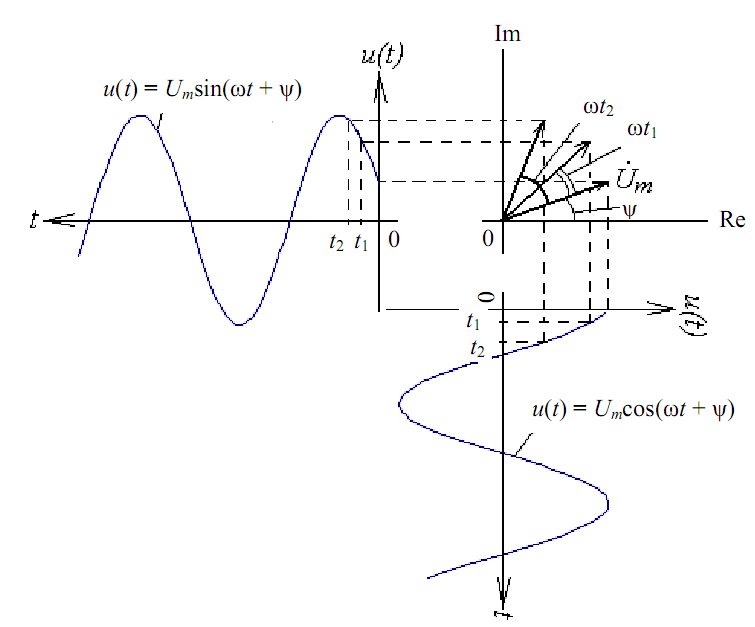
Рис. 1

Проекція вектора на дійсну вісь являє собою миттєве значення, яке виражається косинусоїдальною функцією

а на уявну вісь - синусоїдальної функцією

Символічний вектор на комплексній площині математично може бути представлений в трьох формах:

алгебраічній

показниковій

тригонометричній

У випадку гармонійного коливання аргумент комплексного числа 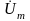є функцією часу

Тому число, що символізує обертається вектор, виражається в показовій формі

в тригонометричній формі

Крім розглянутого вище, можливий і дещо інший спосіб представлення гармонійних коливань у вигляді двох обертових назустріч векторів (рис. 2).

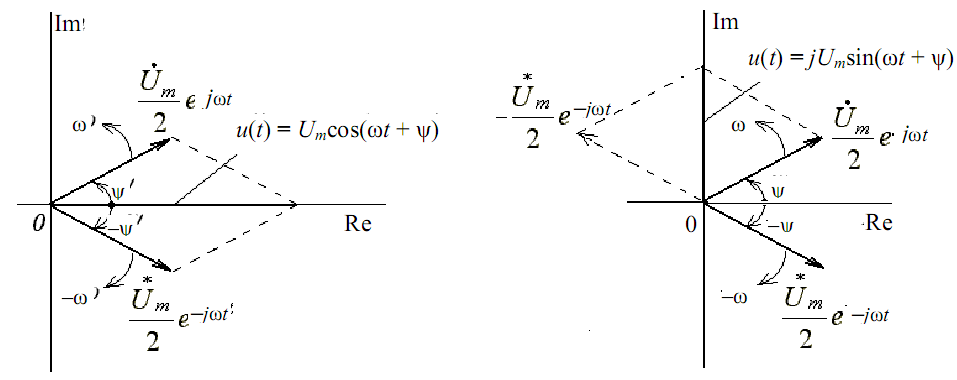
На основі формули Ейлера:

або

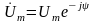де , а - комплексно-спряжене число.

або .

Обертання векторів у від’ємному напрямі (по ходу годинникової стрілки рис. 2) пов'язано з поняттям негативною частоти, що, звичайно, позбавлене фізичного змісту, однак дозволяє спростити вирішення багатьох завдань у радіотехніці та електроніці.

Таким чином, при розгляді напруг і струмів в ланцюзі при гармонійному впливі може бути побудована векторна діаграма, що представляє собою сукупність радіус-векторів, відображають комплексні амплітуди коливань і обертових на комплексній площині проти годинникової стрілки з кутовою швидкістю ω

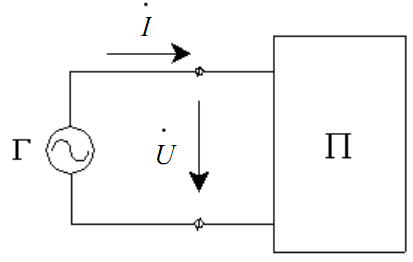
Рис. 3

Оскільки взаємне розташування векторів на діаграмі не змінюється, то зручно розглядати комплексні амплітуди напруг і струмів в момент часу t= 0.

На рис. 3 наведено схематичне зображення ланцюга змінного струму.

Генератор гармонійних коливань живить пасивний двухполюсник, що складається з опорів, індуктивностей і ємностей.

Відношення комплексних амплітуд напруги і струму на вході двухполюсника називається його комплексним вхідним опором:

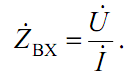
Величина, зворотня комплексному опору, називається його комплексною провідністю

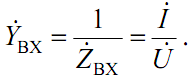
Враховуючи, що та , отримуємо .

Відношення - повний вхідний опір(модуль); - зсув фаз між напругами і струмом.

Як всяке комплексне число, комплексний опір і комплексна провідність можуть бути представлені в показовій, алгебраїчній і тригонометричній формах:

де - реальна активна складова;

- уявна реактивна складова комплексного опору;

Очевидно