19. Основные свойства дпф

Свойство 1. Линейность

, ,

Свойство 2. Периодичность

,

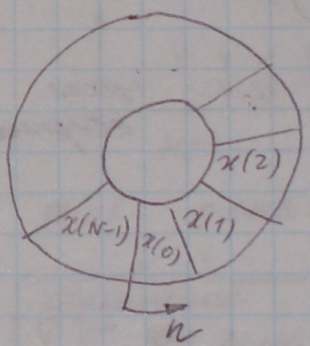
Свойство 3. Свойство сдвига

Если – периодическая с периодом и ее ДПФ , то ДПФ последовательности имеет вид

Свойство 4. Циклическая свертка последовательностей

и – периодические с периодом . Им соответствует ДПФ и . Найдем и вычислим ОДПФ от .

– круговая или циклическая свертка, .

Это нелинейная (апериодическая) свертка .

20. Вычисление линейной апериодической свертки при помощи дпф

Пусть и – две конечные последовательности. Найдем свертку .

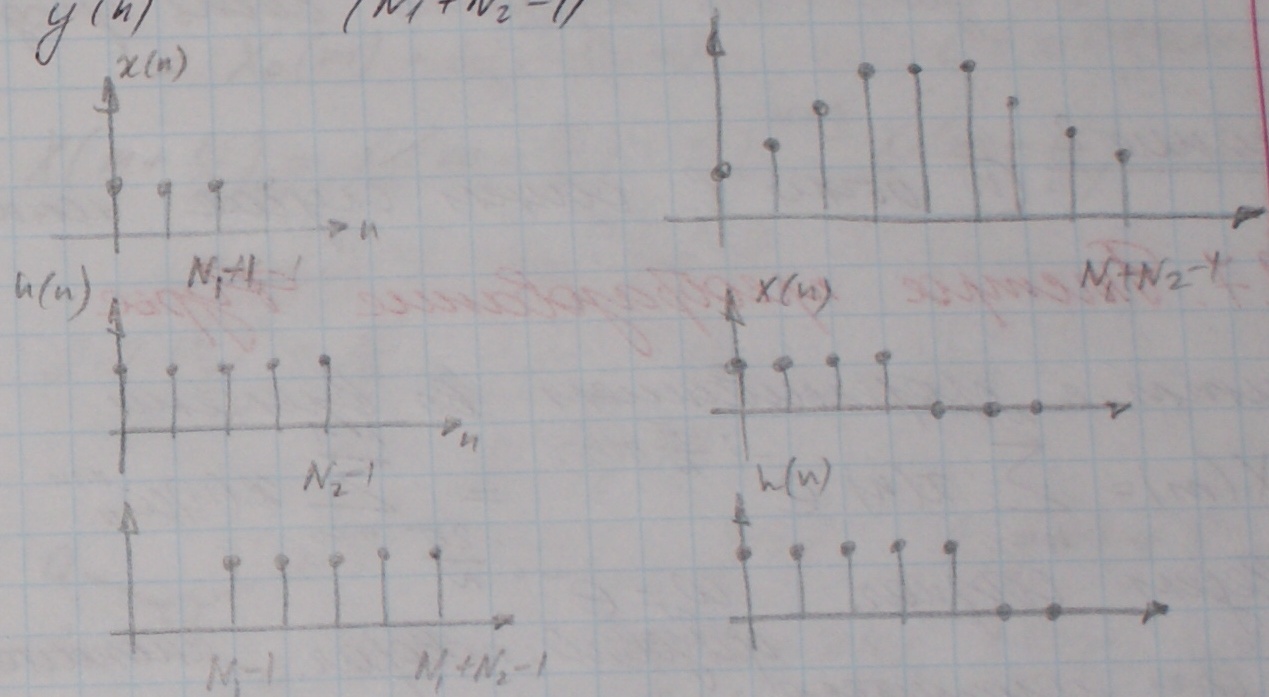
Длина итоговой последовательности составит .

Замечание 1.Последовательность можно дополнять нулями сколь угодно долго.

Замечание 2. В общем случае последовательности и могут быть комплексными.

21. Алгоритм быстрого преобразования Фурье. Оценка эффективности

Алгоритм с прореживанием во времени.

. Введем обозначение . Эта величина называется фазовым, поворачивающим множителем.

Свойства фазового множителя:

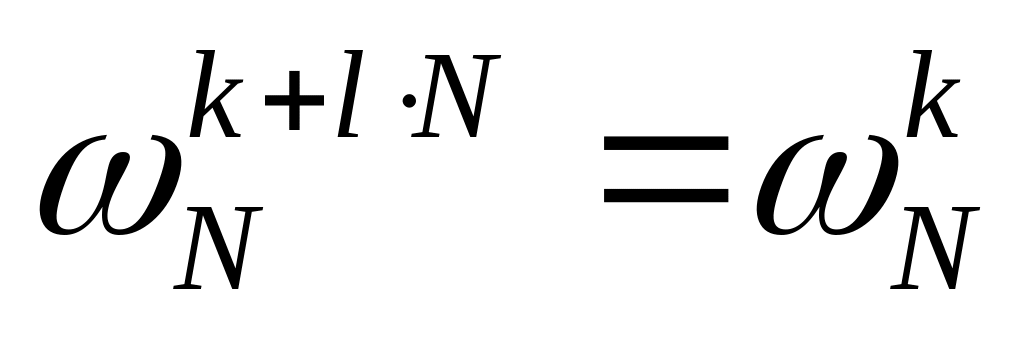1. – периодичность с периодом

2. 

3. 

4. 

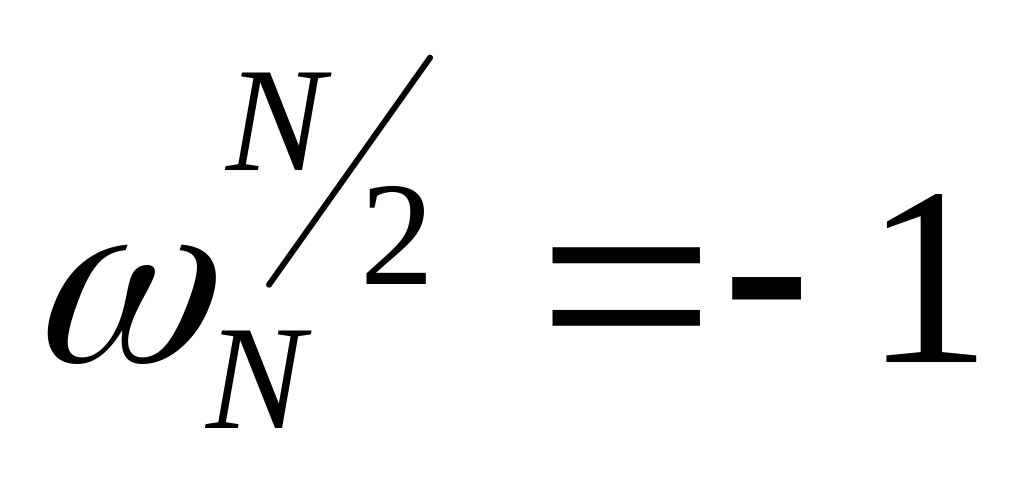
Поскольку дискретный спектр рассматривается в точках ( ), то если вычислять его непосредственно по формуле , потребуется раз выполнить по операций умножений и по операций сложения комплексных чисел. Так как преобразование вычисляется на ЭВМ, то общее вермя его выполнения (без учета служебных операций) равно . Возрастание вычислительной сложности ДПФ, пропорциональное квадрату длины, вызывает необходимость разработки алгоритмов БПФ.

Одна из основных идей БПФ заключается в том, что исходная -точечная последовательность разбивается на несколько более коротких последовательностей, дискретные спектры которых могут быть скомбинированы таким оразом, чтобы в итоге получилось ДПФ полной последовательности.

Разобьем длины на две подпоследовательности, в первую из которых войдут четные, а во вторую – нечетные элементы исходной последовательности:

, , .

Тогда -точечное ДПФ разбивается на два слагаемых:

при . Из свойств фазового множителя . Это позволяет в два раза сократить число используемых значений фазового множителя.

По свойствам спектров .

Окончательно, для

Полученное соотношение определяет операцию объединения «половинных» ДПФ в целое. Ее часто изображают графически.

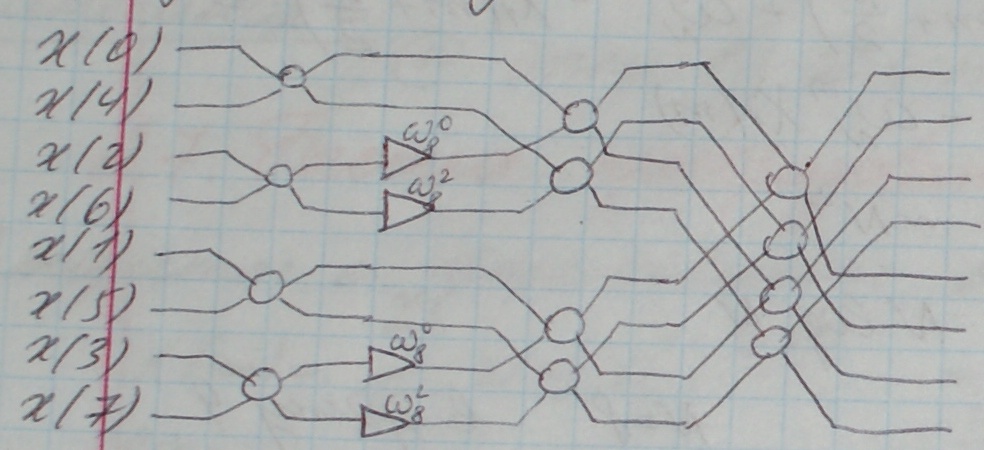
Замечание 1. На входе должны быть в двоично-инверсионном порядке

0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7

Замечание 2. Всё преобразование выполняется на одном и том же мете без использования дополнительной памяти. ,

Замечание 3. Схема БПФ годится и для обратного ПФ – достаточно заменить множитель.

22. Совмещенный алгоритм бпф для двух вещественных последовательностей

Пусть , , , , .

Рассчитаем спектр 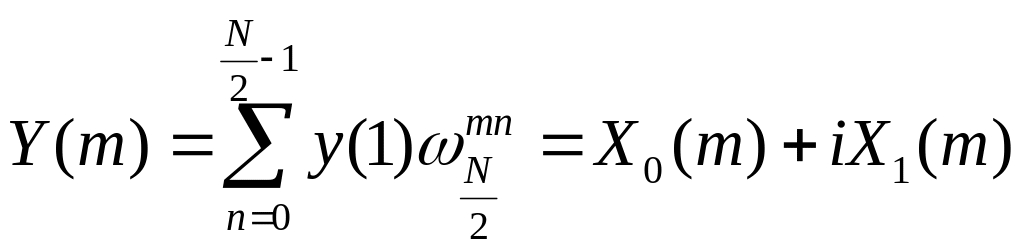, где , . Продолжим спектры и на промежуток : .

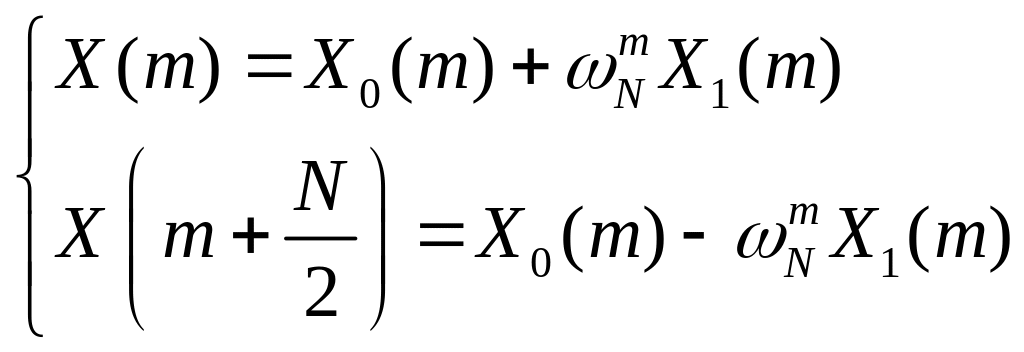Как разделить и в ?

Доказали свойство симметрии дискретного спектра вещественной последовательност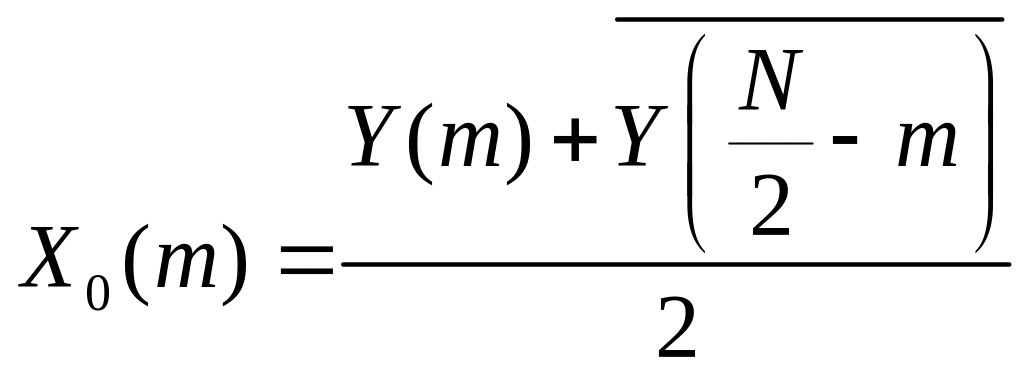и:

, , и