13. Методы вычисления обратного z-преобразования. Примеры.

Умножим обе части уравнения на и проинтегрируем их по , выбрав контур так, чтобы он полностью лежал внутри области сходимости -преобразования: .

Из интегральной теоремы Коши следует, что , где интеграл берется против часовой стрелки по замкнутому контуру , охватывающему начало координат комплексной -плоскости.

Тогда . Откуда обратное -преобразование имеет вид: , где –контур, окружающий начало координат с направлением обхода против часовой стрелки и расположенный в области сходимости .

Если подынтегральная функция является аналитической во всей внутренней области контура, за исключением конечного числа особых точек, то по теореме о вычетах интеграл определяется через сумму вычетов:

, где – число особых точек внутри контура , – особые точки, – -кратный вычет функции в точке . Он вычисляется так:

где – функция, не имеющая особенностей (аналитическая) в точке .

Пример: вычислить последовательность, соответствующую -преобразованию, с областью сходимости .

Решение:

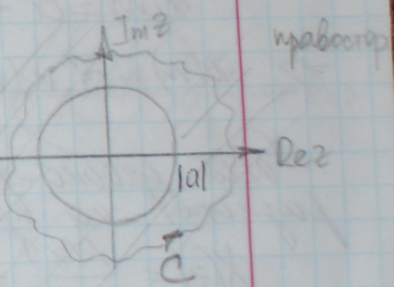
. При единственный полюс , .

При есть два полюса: простой и кратности . , будем вычислять при разных значениях :

При :

При :

При :

Тогда . В итоге получили

На практике приводят к представлению в виде суммы простых функций, обратные -преобразования которых известны. Для дробно-рациональной функции , где , и – полиномы от , – общее число полюсов, – кратность полюса , . – целая часть , в случае, если степень не меньше . Постоянные находятся методом неопределенных коэффициентов. Каждая из дробей соответствует последовательности правосторонней, если и левосторонней, если . Область сходимости такого элементарного -преобразования будет определяться сооветственно неравенством или .

Пример: вычислить последовательность, соответствующую -преобразованию , с областью сходимости .

Решение:

. Полюсы: , . Представим дробь в виде суммы двух дробей: . Найдем коэффициенты и : . Тогда .

. Полюс , , . . Полюс , . Найдем .

Рассмотрим . Для него областью сходимости будет , , откуда . Так как , то . Тогда окончательно .

14. Анализ и синтез одномерных лис-систем с использованием z-преобразования. Исследование устойчивости.

Передаточная функция дискретной ЛПП-системы есть -преобразование ее импульсной характеристики:

. Свертку можно записать -область в виде , где , – -преобразования выходной и входной последовательностей. Область сходимости состоит как минимум из пересечения областей сходимости и .

Разностное уравнение можно записать в преобразованной форме: . Отсюда находим передаточную функцию: , откуда .

Область сходимости дробно-рационального -преобразования ограничена полюсами. Если ЛПП-система физически реализуема, т.е. ее импульсная характеристика является правосторонней последовательностью, удовлетворяющей условию при , то область сходимости передаточной функции – внешняя часть круга, проходящего через наиболее удаленный от начала координат полюс. Такая система устойчива, если все полюсы ее передаточной функции лежат внутри единичной окружности.

Утверждение. Если ЛИС-система допускает представление в виде разностного уравнения конечного порядка, то она всегда имеет дробно-рациональную передаточную функцию.