1. Одномерные последовательности. Их классификация и способы задания

Два способа записи последовательности:

– отражает процесс дискретизации непрерывного во времени сигнала, где .

короче и используется в случае, когда не требуется учитывать реальный масштаб времени.

Интервал определения последовательности может быть

• Конечным: , где , 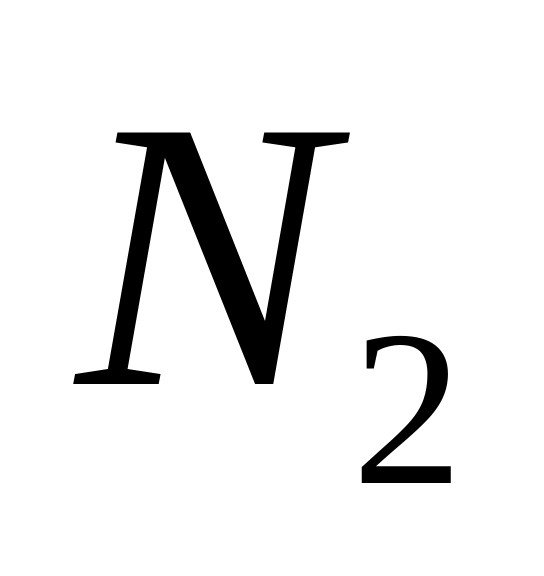– целые. Имееп последовательность конечной длины

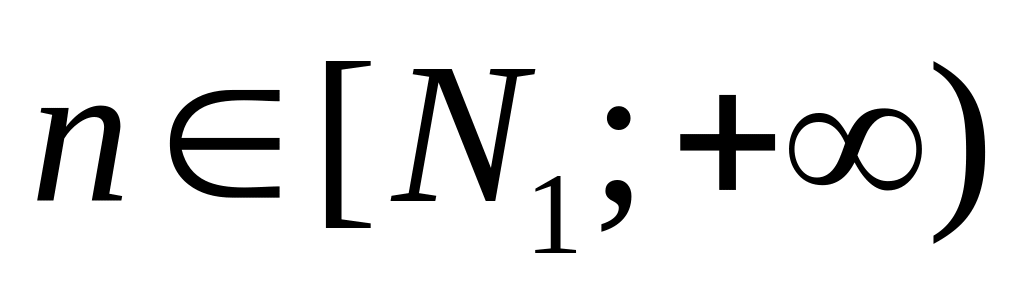• Полубесконечным: – левосторонняя или – правосторонняя

• Бесконечным: 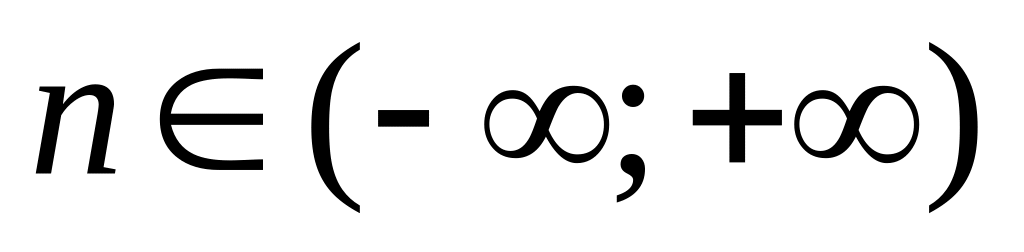– двусторонняя.

Для унификации всякую последовательность обычно приводят к бесконечной, полагая отсчеты, лежащие вне интервала определения, тождественно равными нулю.

Последовательность называется детерминированной, если можно точно указать ее значение для любого момента дискретного времени .

Последовательность – случайная, если ее элементы – случайные величины.

Способы задания детерминированной последовательности:

1. Задание значений:

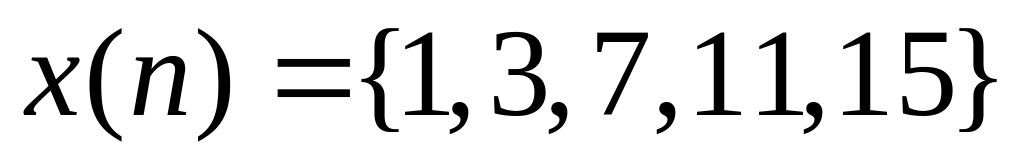
2. Аналитическое задание:

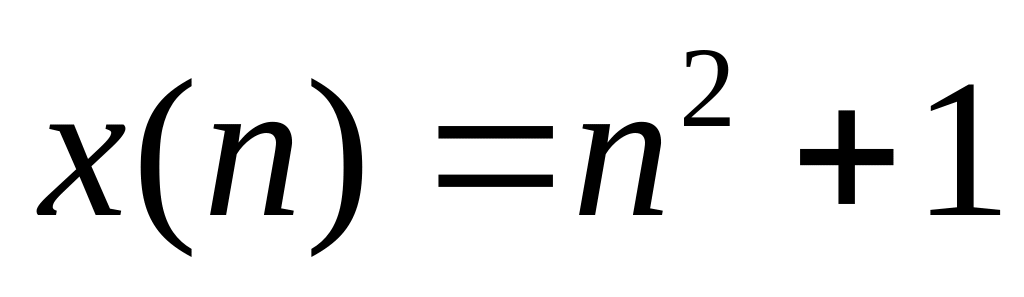
3. Аналитически через дискретизированную функцию:

4. Через рекуррентную функцию: ,

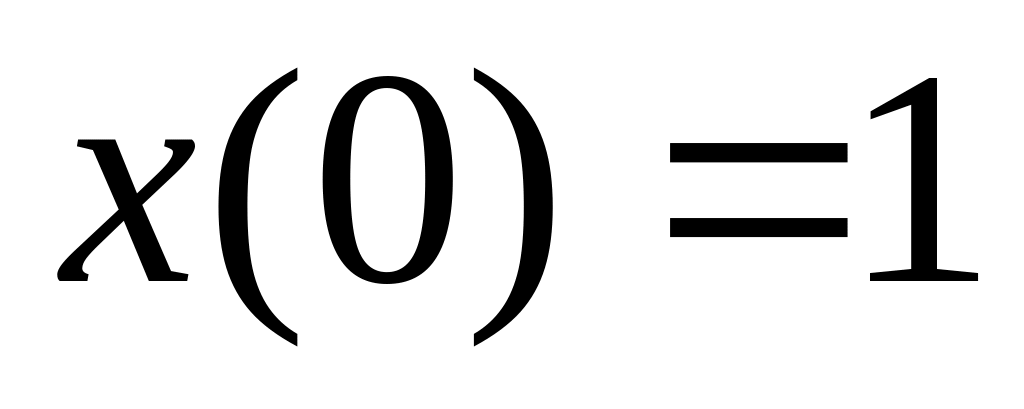
5. Графический способ:

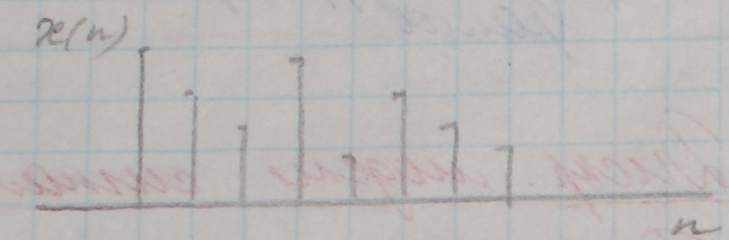
Примеры последовательностей:

1. Единичный импульс:

2. Единичный скачок:

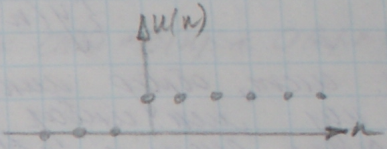
3. Дискретная правосторонняя экспонента:

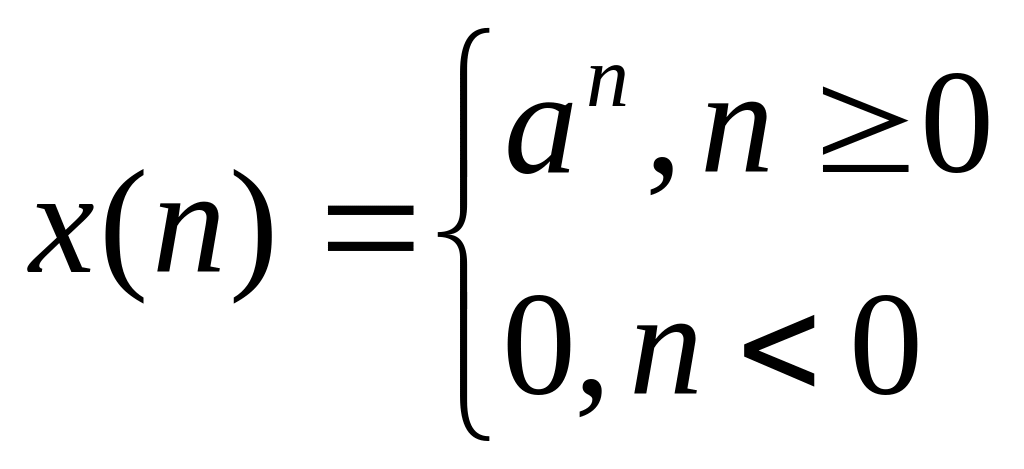
4. Дискретная комплексная экспонента: , где , имеющая смысл безразмерной частоты

2. Дискретные лис-системы. Импульсная характеристика.

Опр. Дискретной системой будем называть некоторое правило , по которому входная последовательность преобразовывается в выходную последовательность : .

Опр. Дискретная система называется линейной, если для нее соблюдается принцип суперпозиции: .

Опр. Дискретная система называется системой с постоянными параметрами, если выполняется , то есть если она обладает свойством инвариантности ко времени.

Опр. Дискретные системы, обладающие одновременно свойствами линейности и инвариантности к сдвигу, называются дискретны­ми линейными системами с постоянными параметрами (ЛПП-системами).

Чтобы описать систему с информационной точки зрения, нужно указать конкретное правило преобразования входного сигнала в выходной. ЛПП-систему можно описать с помощью ее импульсной характеристики.

Опр. Импульсная характеристика дискретной ЛПП-системы определяется как реакция системы на входное воздействие в форме единичного импульса: .

Полная выходная последовательность записывается в виде свертки: .

Свойства свертки :

1. Коммутативность: ;

2. Ассоциативность:

3. Дистрибутивность:

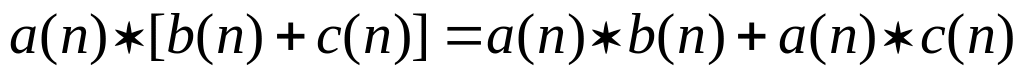
4. Фильтрующее свойство единичного импульса:

5. Свободное суммирование сдвига. Если ,

6. Для ЛПП-системы при последовательном соединении звеньев с ИХ :

7. Для ЛПП-системы при параллельном соединении звеньев с ИХ : .

3. Физическая реализуемость лис-систем.

Опр. Дискретная система называется физически реализуемой, если значение выходной последовательности в произ­вольный момент зависит только от значений входной последовательности при .

Для физически реализуемой системы отклик не опережает входное воздействие.

. Для физической реализуемости должно быть при , . Отсюда необходимое и достаточное условие физической реализуемости ЛПП-системы: при .