3) Найти ранг матрицы
Решение. С помощью элементарных преобразований над ее строками приведем матрицу А к ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:
От второй строки отнимаем четвертую строку, умноженную на 4; от третьей - две четвертых:
Ко второй строке прибавим пять первых, к третьей - три третьих:
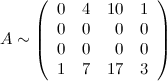
Меняем местами первую и вторую строчки:
Далее четвертую и первую строки:
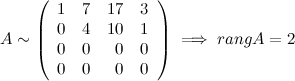
Билет № 29
1) Привести свойства операций сложения матриц и умножения матрицы на число.
Сложение матриц Сложение: операция сложения матрицы вводится только для матриц одинаковых размеров.
Суммой
двух матриц
и
называется матрица
такая, что
,
например,
,
, тогда
Аналогично определяется разность матриц.
Умножение
матрицы на число
Произведением
матрицы
на число k называется матрица
такая, что
,
Примечание:
матрица
называется противоположной матрице
A
.
Операции сложения и умножения матрицы на число обладают следующими свойствами:
1)
;
2)
3
)
;
4)
;
5)
;
6)
;
7)
;
8)
.
2) Дать понятие безусловного экстремума функции нескольких переменных
Рассмотрим
вопрос о нахождении экстремума функции
многих переменных
.
Определение.
Говорят, что в точке
функция
имеет локальный максимум (минимум),
если
Термины «локальный максимум» и «локальный минимум» объединяют в один термин «локальный экстремум». Необходимые условия экстремума. Необходимые условия экстремума дает теорема Ферма. В применении к нашему случаю, они имеют такой вид: если в точке функция имеет локальный максимум (минимум), то в ней выполняется условие
или,
сокращенно,
Достаточные условия экстремума. Выполнение написанных выше условий не гарантирует, что в точке функция имеет локальный экстремум; кроме того, даже если там имеет место локальный экстремум, то надо установить его тип – максимум или минимум. Ответ на этот вопрос выглядит следующим образом.
Надо
построить матрицу А размерности n´n c
элементами
и, используя критерий Сильвестра, установить, какая она – положительно определенная, отрицательно определенная или неопределенная (что такое положительно определенная, отрицательно определенная или неопределенная матрица и критерий Сильвестра Вы должны знать из курса алгебры). Тогда если матрица А положительно определенная, то в точке функция имеет локальный минимум; если матрица А отрицательно определенная, то в точке функция имеет локальный максимум; если матрица А неопределенная, то в точке функция не имеет локального экстремума (это – так называемая седловая точка).
3) Найти ранг матрицы , используя метод окаймления миноров.
Решение.
Минорами минимального порядка являются
миноры первого порядка, которые равны
элементам матрицы A.
Рассмотрим, например, минор
. расположенный в первой строке и первом
столбце. Окаймляем его с помощью второй
строки и второго столбца, получаем минор
; рассмотрим еще один минор второго
порядка, для этого минор
окаймляем при помощи второй строки и
третьего столбца, тогда имеем минор
, то есть ранг матрицы не меньше двух.
Далее рассматриваем миноры третьего
порядка, которые окаймляют минор
. Таких миноров два: комбинация третьей
строки со вторым столбцом или с четвертым
столбцом. Вычисляем эти миноры:
так
как содержит два пропорциональных
столбца (первый и второй); второй минор
преобразуем
следующим образом: к первой строке
прибавим третью, а ко второй две третьих:
И так как первая и вторая строки пропорциональны, то минор равен нулю.
Таким
образом, все окаймляющие миноры третьего
порядка равны нулю. А, значит, ранг
матрицы A
равен двум:
Билет № 30 1)Дать определение степени матрицы.
Степень матрицы – это матрица, полученная путём многократного умножения на саму себя: Аn = А А А А …А (n раз) Частный случай умножения: одна из матриц-сомножителей имеет один столбец или одну строку. Если считать матрицу строку или матрицу-столбец формой представления вектора, то мы получаем правило умножения матрицы на вектор.
Пример. Матрица А Матрица В Матрица АВ
12 3 1 1*1 + 2*2 + 3*3 = 14
45 6 2 4*1 + 5*2 + 6* 3 = 32
7 8 9 3 7*1 + 8*2 +9*3 =50