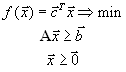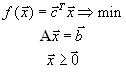3 Вопрос

Умножение матрицы на число: Пусть   . Найти матрицу 

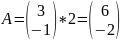
Билет № 14

1)Произведение матрицы А порядка p*n и матрицы В порядка n*q - это такая матрица С порядка p*q, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В, то есть,

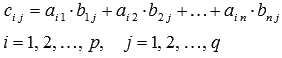
П ример

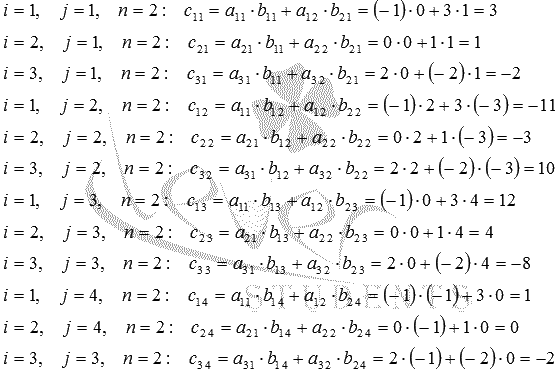
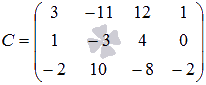
2) Определение. Условным экстремумом функции z  = f (х, у) называется экстремум этой функции, достигнутый при условии,  что переменные х и у связаны уравнением (х, у) = 0 (уравнением связи). Определение 7.4   Пусть функция   определена в некоторой окрестности ,  , некоторой точки   своей области определения. Точка   называется точкой локального максимума, если в некоторой такой окрестности  выполняется неравенство  (  ), и точкой локального минимума, если    . Если точка   -- это точка локального экстремума функции  , и существует производная в этой точке  , то . Наименьшее (наибольшее) значение функции в данной области называется абсолютным экстремумом функции в этой области. необходимое условие    Если точка   -- это точка локального экстремума функции  , и существует производная в этой точке  , то

3.

Билет №16

№1Задачи оптимального планирования, связанные с отысканием оптимума заданной целевой функции (линейной формы) при наличии ограничений в виде линейных уравнений или линейных неравенств относятся к задачам линейного программирования.

Линейное программирование - наиболее разработанный и широко применяемый раздел математического программирования.

Итак, Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием.

Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.

Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функцииF, называется оптимальным планом задачи.

Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального).

В общей постановке задача линейного программирования выглядит следующим образом:

Имеются какие-то переменные х = (х₁ , х₂ , … х_n ) и функция этих переменных f(x) = f (х₁ , х₂ , … х_n ), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:

В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что  а) функция f(x) является линейной функцией переменных х₁ , х₂ , … х_n б) область G определяется системой линейных равенств или неравенств.

Математическая модель любой задачи линейного программирования включает в себя:

• максимум или минимум целевой функции (критерий оптимальности);

• систему ограничений в форме линейных уравнений и неравенств;

• требование неотрицательности переменных.

№2 Метод наискорейшего спуска Название метода можно было бы понимать буквально, если бы речь шла о минимизации целевой функции. Тем не менее по тра диции такое название используется и при решении задачи на максимум. Пусть f(x)=f(x₁,x₁,...x_n) —дифференцируемая функция, заданная на Rⁿ, а х^(q) = (x₁^(q),x₂^(q),...,x_n^(q)) — некоторая текущая точка. Оговоримся, что каких-либо общих рекомендаций, каса ющихся выбора исходной точки (или, как еще говорят, началь ного приближения) х⁽⁰⁾, не существует, однако по возможно сти она должна находиться близко от искомого оптимального плана х*. Как уже говорилось выше, если х^(q) — нестационарная точка (т. е. |f(x^(q))|>0), то при движении в направлении f(x^(q)) функция f(х) на некотором промежутке обязательно будет возрастать. Отсюда возникает естественная идея такого выбора шага, чтобы движение в указанном направлении продол жалось до тех пор, пока возрастание не прекратится. Для этого выразим зависимость значения f(x) от шагового множителя λ > 0. полагая х = х^(q) + λf(x^(q)) или, в координатной форме, Чтобы добиться наибольшего из возможных значений f при движении по направлению f(x^(q)), нужно выбрать такое значе ние , которое максимизирует функцию φ(λ) (φ()= max(φ(λ)). Для вычисления , используется необходимое условие экстре мума dφ(λ)/dλ = 0. Заметим, что если для любого λ>0 dφ()/dλ> 0, то функция f(х) не ограничена сверху (т. е. не име ет максимума). В противном случае, на основе (2.10) получаем  что, в свою очередь, дает Если считать, что следующая точка х^(q+1) соответствует оптимальному значению λ=, то в ней должно выполняться условие dφ()/dλ = 0, и  следует находить из условия f(x^(q+1)) f(x^(q))=0 или Условие (2.13) означает равенство нулю скалярного про изведения градиентов функции f точках x^(q+1) и x^(q). Гео метрически оно может быть интерпретировано как перпенди кулярность векторов градиентов функции f в указанных точ ках, что и показано на рис. 2.2. Продолжая геометрическую интерпретацию метода наискорейшего спуска, отметим, что в точке x^(q+1) вектор f(x^(q+1)), будучи градиентом, перпендику лярен линии уровня, проходящей через данную точку. Стало быть, вектор f(x^(q)) является касательным к этой линии. Итак, движение в направлении градиента f(x^(q)) следует продолжать до тех пор, пока он пересекает линии уровня оп тимизируемой функции. После того как точка x^(q+1) найдена, она становится текущей для очередной итерации. На практике признаком достижения стационарной точки служит достаточно малое изменение коор динат точек, рассматриваемых на последовательных итераци ях. Одновременно с этим координаты вектора Δf(x^(q)) должны быть близки к нулю.

№3 Задание. Вычислить   и  , если 

Решение. Так как   , а   , то произведение возможно и результатом операции умножения будет матрица   , а это матрица вида   .

Вычисли элементы матрицы   :

Итак,   .

Выполним произведения в более компактном виде:

Найдем теперь произведение  . Так как количество столбцов матрицы  (первый сомножитель) не совпадает с количеством строк матрицы   (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.

Ответ.   . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы   не совпадает с количеством строк матрицы   .

БИЛЕТ 18

1. Привести запись двойственных друг другу задач в матричной форме.

Симметричные двойственные задачи

Рассмотрим задачу линейного программирования в стандартной форме

(1)

,

или, в матричной форме,

(2)

Рассмотрим теперь следующую задачу

(3)

,

или, в матричной форме,

(4)

Пара задач (1) и (3) (или, в матричной форме, пара задач (2) и (4) ) называются двойственными друг другу задачами в симметричной форме.

Несимметричная двойственная задача

Исходная задача имеет вид:

(5)

,

или, в матричной форме,

(6)

Двойственная задача в несимметричной форме имеет вид

(7)

 

или, в матричной форме,

(8)

Обратите внимание на то, что в несимметричной двойственной задаче не накладывается условие неотрицательности переменных.

Если исходная задача линейного программирования записана в произвольной форме, то для записи двойственной задачи следует сначала записать исходную задачу в канонической или стандартной форме, а затем выписать двойственную задачу. При желании, получившуюся двойственную задачу также можно привести к какой-либо нестандартной форме.

2) Что изучает раздел стохастического программирования? Стохасти́ческое программи́рование — это подход, позволяющий учитывать неопределённость в оптимизационных моделях.

В то время как детерминированные задачи оптимизации формулируются с использованием заданных параметров, реальные прикладные задачи обычно содержат некоторые неизвестные параметры. Когда параметры известны только в пределах определенных границ, один подход к решению таких проблем называется робастной оптимизацией. Этот подход состоит в том, чтобы найти решение, которое является допустимым для всех таких данных и в некотором смысле оптимально.

Модели стохастического программирования имеют подобный вид, но используют знание распределений вероятностей для данных или их оценок. Цель здесь состоит в том, чтобы найти некоторое решение, которое является допустимым для всех (или почти всех) возможных значений данных и максимизируют математическое ожидание некоторой функции решений и случайных переменных. В общем, такие модели формулируются, решаются аналитически или численно, их результаты анализируются, чтобы обеспечить полезную информацию для лиц, принимающих решения.

Наиболее широко применяются и хорошо изучены двухэтапные линейные модели стохастического программирования. Здесь лицо, принимающее решение, предпринимает некоторое действие на первом этапе, после которого происходит случайное событие, оказывающее влияние на результат решения первого этапа. На втором этапе может тогда быть принято корректирующее решение, которое компенсирует любые нежелательные эффекты в результате решения первого этапа.

Оптимальным решением такой модели является единственное решение первого этапа и множество корректирующих решений (решающих правил), определяющих, какое действие должно быть предпринято на втором этапе в ответ на каждый случайный результат.

2. ранспонирование матрицы: Найти матрицу  , если

Решение

=>

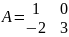Билет № 19

1. Дать понятие линейной зависимости системы векторов. 2) Сформулировать принцип оптимальности. 3) Найти минор   к элементу 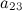  определителя   .

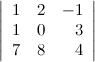Зав. кафедрой

1) Выражение видаλ₁*A₁+λ₂*A₂+...+λ_n*A_n называется линейной комбинацией векторов A₁, A₂,...,A_n с коэффициентами λ_1, λ₂,...,λ_n.

Определение линейной зависимости системы векторов

Система векторов A₁, A₂,...,A_n называется линейно зависимой, если существует ненулевой набор чисел λ_1, λ₂,...,λ_n, при котором линейная комбинация векторов λ₁*A₁+λ₂*A₂+...+λ_n*A_n равна нулевому вектору, то есть система уравнений: A₁x₁+A₂x₂+...+A_nx_n =Θ имеет ненулевое решение. Набор чисел λ_1, λ₂,...,λ_n является ненулевым, если хотя бы одно из чисел λ_1, λ₂,...,λ_n отлично от нуля.

Определение линейной независимости системы векторов

Система векторов A₁, A₂,...,A_n называется линейно независимой, если линейная комбинация этих векторов λ₁*A₁+λ₂*A₂+...+λ_n*A_n равна нулевому вектору только при нулевом наборе чисел λ_1, λ₂,...,λ_n, то есть система уравнений: A₁x₁+A₂x₂+...+A_nx_n =Θ имеет единственное нулевое решение.

2)Беллмана принцип оптимальности БЕЛЛМАНА ПРИНЦИП ОПТИМАЛЬНОСТИ [Bellman’s optimality principle] — важнейшее положение динамического программирования, которое гласит: оптимальное поведение в задачах динамического программирования обладает тем свойством, что каковы бы ни были первоначальное состояние и решение (т. е. “управление”), последующие решения должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения. Этот принцип можно выразить и рассуждая от противного: если не использовать наилучшим образом то, чем мы располагаем сейчас, то и в дальнейшем не удастся наилучшим образом распорядиться тем, что мы могли бы иметь. Следовательно, если имеется оптимальная траектория, то и любой ее участок представляет собой оптимальную траекторию. Этот принцип позволяет сформулировать эффективный метод решения широкого класса многошаговых задач. (Подробнее см. Динамическое программирование.) Принцип назван по имени крупного американского математика Р. Беллмана, одного из основоположников динамического программирования.

3) =1*3-(-1*1)=4

Билет №20