Частина ііі. Приклади розв’язку типових завдань

І. Невизначений інтеграл.

а) Обчислити інтеграл:

Розв’язування:

б) Обчислити інтеграл: .

(Враховано, що )

в) Обчислити інтеграл:

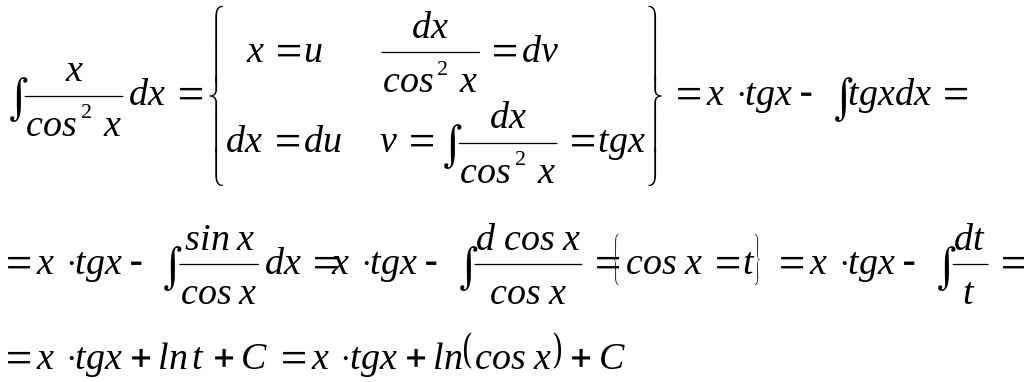
(Використана формула інтегрування частинами).

г) Обчислити інтеграл:

(Використана формула інтегрування частинами ).

д) Обчислити інтеграл:

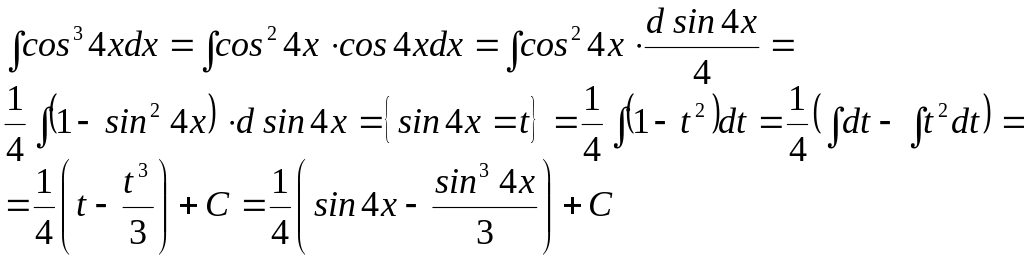
е) Обчислити інтеграл:

є) Обчислити інтеграл:

Використана формула:

а також парність функції :

ж) Обчислити інтеграл:

Обчислимо коефіцієнти А і В.

Нехай .

Нехай х=-3.

Отже, ; С- довільна константа.

з) Обчислити інтеграл:

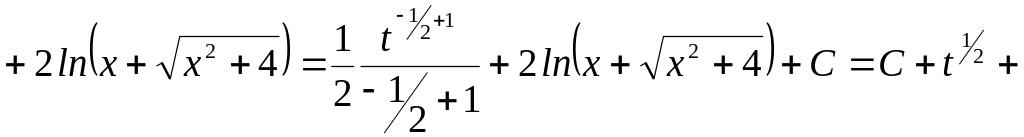
і) Обчислити інтеграл:

к) Обчислити інтеграл:

ІІ. Визначений інтеграл.

1. Обчислити: .

Розв’язування:

Тоді. . Отже підінтегральний вираз можна записати у вигляді: .

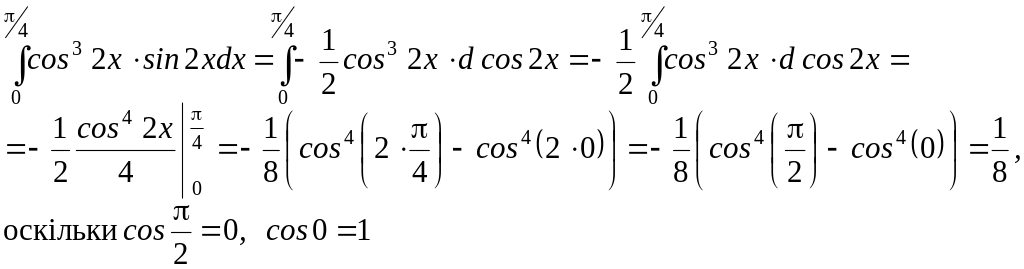
2. Обчислити: . Інтеграл будемо обчислювати частинами з використанням формули: .

3. Обчислити: . Підінтегральна функція є правильним дробом, тому її можна записати як суму простих дробів:

, де А, В, С – числа.

Тоді: =

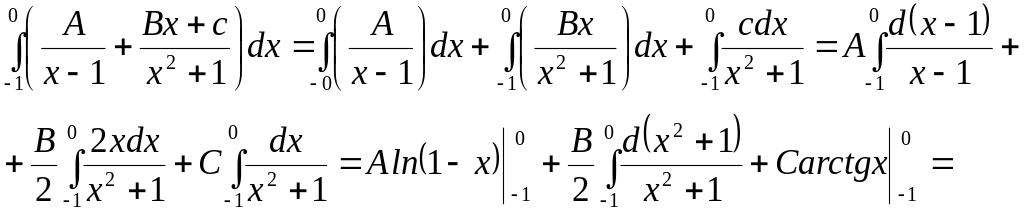
Обчислимо А, В, С. Помножимо обидві частини рівності (а) на х-1. Одержимо: (б)

Рівність (б) виконується при . Нехай в (б) х=1. Одержимо:

.

Для обчислення В і С рівність (а) приводимо до спільного знаменника, після чого прирівнюємо чисельники та одержуємо:

, але А=1, тому:

(в)

Остання рівність виконується для , тому коефіцієнти при однакових степенях х лівої та правої частин (в) повинні співпадати.

Випишемо рівності коефіцієнтів при .

.

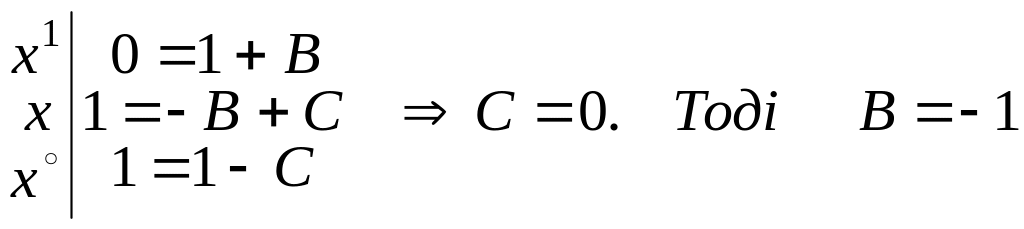Отже, А=1, В=-1, С=0. Підставивши ці значення у Відповідь , яку ми отримали при обчисленні інтеграла одержимо:

4. Обчислити: .

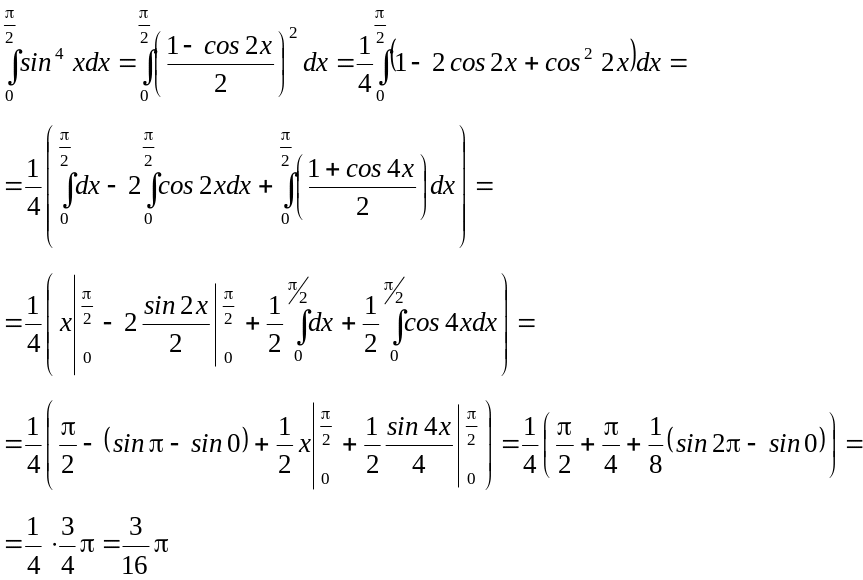
При обчисленні даного інтеграла використані формули тригонометрії

5. Користуючись теоремою про оцінку інтеграла, оцінити інтеграл:

Функція - монотонно зростає при х>0. Функція - також монотонно зростає, тому знаменник підінтегральної функції монотонно зростає, а чисельник – стала величина. Звідси випливає, що підінтегральна функція монотонно спадає на відрізку [0,4], тому максимальне значення вона має в т.х=0, а мінімальне в т. х =4. Отже, М = maxf(x):

За теоремою про оцінку інтеграла:

В даному конкретному прикладі b – a = 4 – 0 = 4. Тому:

6. Обчислити середнє значення функції:

на [0;4].

За теоремою про середнє значення f(c) функції f(х) на [а;b] , обчислюється за формулою:

В даному прикладі середнє значення f(c) дорівнює:

7. Обчислити площу фігури, обмеженої лініями: Зробити схематичний малюнок (схематичне креслення).

Розв’язування. Графік функції – парабола з вершиною у точці х=0, у=2, гілки параболи донизу. Знайдемо точки перетину ліній .

Позначимо площу заштрихованої фігури S:

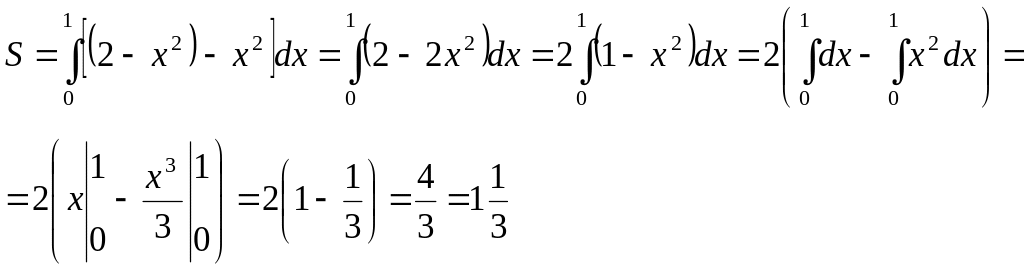
8. Фігура, обмежена лініями обертається навколо осі Ох. Обчислити об’єм тіла обертання.

Розв’язування.

.

якщо обертається заштрихована на рисунку фігура:

У даному прикладі . Тому:

9. Дослідити на збіжність інтеграл по нескінченному проміжку:

Можна знайти первісну підінтегральної функції.

Висновок: інтеграл збіжний, так як він дорівнює кінцевому числу.

10. Дослідити на збіжність інтеграл від розривної функції:

. Первісну підінтегральної функції обчислити можна, але простіше скористатись ознакою збіжності невластивого інтеграла. Беремо для порівняння функцію:

.

Обчислимо границю відношення підінтегральної функції і при :

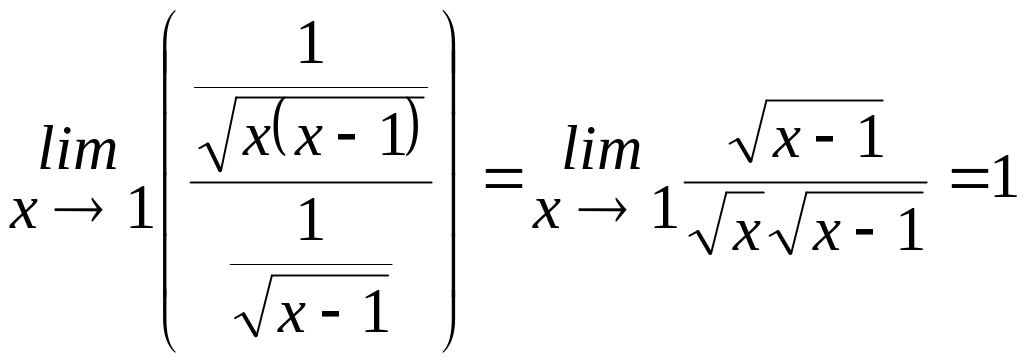
тобто, тому за ознакою збіжності – збіжний

11. Обчислити точне та наближене значення інтеграла за формулою прямокутників та формулою Сімпсона. розбивши проміжок інтегрування на 10 частин. Обчислити абсолютну та відносну в % похибку наближених значень.

Розв’язування. Обчислимо точне значення інтеграла:

Для обчислення наближених значень інтеграла розіб’ємо проміжок [0,1] на 10 однакових за довжиною частин. Вставивши точки розбиття х_і (і=0,1,2,3,...10), .

Складемо таблицю х_і та , де – підінтегральна функція. У даному прикладі , тоді :

і
	0										1
	0,5	0,476	0,454	0,435	0,417	0,4	0,385	0,370	0,357	0,345	0,333

Обчислимо наближене значення інтеграла за формулою прямокутників:

Одержимо:

Обчислимо наближене значення інтеграла за формулою Сімпсона (n=2m)

Одержимо:

Обчислимо похибки наближених значень.

Абсолютна похибка формули прямокутників:

∆

Відносна похибка формули прямокутників:

∆

Абсолютна похибка формули Сімпсона:

∆ = 0,405 – 0,403 = 0,002

Відносна похибка формули Сімпсона:

Отже, ми бачимо, що формула Сімпсона дає більш точний результат ніж формула прямокутників.

є) Обчислити подвійний інтеграл:

: