Элементы сетевого планирования

1. Основные понятия.

При планировании и оперативном управлении сложными комплексами работ, объединенных общностью цели, с успехом используются их графические модели – сетевые графики (сети).

1. Понятие сети.

Если элементам графа поставить в соответствие некоторые параметры, то получим сеть.

Параметры могут быть заданы вершинами или (и) дугами графа.

Орграф превращается в сеть, если каждой вершине U_i поставлено в соответствие некоторое число d_i, называемое интенсивностью вершины, а каждой дуге (V_i,V_j) – неотрицательное число r_ij, называемое ее пропускной способностью.

Понятие сети лежит в основе системы сетевого планирования и управления (СПУ).

2. Сетевая модель и ее элементы

Сетевой график – это ориентированный граф без контуров, дуги которого имеют одну или несколько числовых характристик.

Дугами изображаются работы, а вершинами – события.

Работа – любой трудовой процесс или действие, сопровождающиеся затратами времени и ресурсов.

Под работами подразумеваются:

• Не только реальные хоз. или технологические процессы, требующие затрат времени и ресурсов, но и

• Процессы, потребляющие только время (напр., сушка материалов, затвердение бетона и др.) Это так называемые фективные работы – они показывают, что одна работа не может совершаться раньше другой.

На сетевых графиках фиктивные работы обычно изображаются пунктирными стрелками (- - →).

Событие – итог того или иного процесса, промежуточный или окончательный результат выполнения одной или нескольких предшествующих работ, который позволяет к последующим.

Событие совершается тогда, когда закончены все предшествующие ему работы.

Оно становится предпосылкой для начала следующих за ним работ.

Отсюда, событие обладает свойством «сшивания» предыдущих работ с последующими.

Предполагается, что событие не имеет продолжительности и совершается как бы мгновенно.

Каждое событие, включенное в сетевой график, должно быть полно, точно и всесторонне определено, формулировка его должна включать результат выполнения непосредственно предшествующих ему работ.

События изображаются точками, кружками, ромбами и т.д. – это вершины соответствующего графа.

Событие считается совершившимся только тогда, когда будет закончена самая длинная из всех входящих в него работ.

Внутренняя взаимосвязь между работами в графике определяется соблюдением основного правила: все работы взаимосвязаны. Начало последующей обусловлено окончанием предыдущей. Не может быть события, наступление которого не означало бы окончания, по крайней мере, одной работы и тем не менее начала другой. Исключение составляют исходное и завершающее события.

Путь – это любая непрерывная логическая (технологическая) последовательность работ от исходного до завершающего, т.е. от начала разработки до конечной цели.

Здесь важно:

• Ни один путь не может проходить дважды одно и то же событие;

• любой путь может проходить по холостой работе;

• несколько путей могут проходить через одной и то же событие;

Длина пути – определяется суммой продолжительности лежащих на нем работ.

От исходного события до завершающего может быть много путей.

В результате составления и анализа сетевого графика выявляется такой путь, суммарная продолжительность работ на котором будет максимальной – так называемый критический путь – он определяет (обуславливает) время, необходимое для выполнения всех работ, включенных в сетевой график.

Все работы, лежащие на критическом пути, также являются критическими.

Они – потенциально узкое место плана.

В сети можно найти несколько критических путей.

Пути, близкие по времени и критич., называются подкритическими, остальные ненапряженными или некритическими.

Любой некритический путь имеет резерв времени, который равен разности между длительностью критического пути и некритического.

Работы, лежащие на критическом пути, также обладают резервом времени, т.е. они допускают сдвиги в сроках выполнения.

Наличие резервов времени у некритических работ дает возможность свободно маневрировать внутренними ресурсами и этим ускоряет выполнение критических и подкритических работ – это главное в сетевом методе планирования и управления.

3. Виды сетевых моделей

Могут быть использованы 3 основных вида сетевых моделей:

1. в терминах событий, в которых события изображаются вершинами графа, а дуги показывают взаимосвязь отдельных событий;

2. в терминах работ, в которых работы будут вершинами графа, а дуги показывают взаимосвязь отдельных работ;

3. в терминах работ и событий, - в которых работы – это дуги, а события – вершины.

По числу завершающих событий сетевые графики делятся на одно- и многоцелевые.

4. Построение сетевых графиков

Существует несколько общих правил построения сетевых графиков:

а) от начала к кону (от исходного события к завершающему)

б) от середины к концу и началу

в) от конца к началу.

Чаще всего – наиболее распространенный метод – а) – от начала к концу, слева направо.

Каждое событие с большим порядковым номером показывается несколько правее предыдущего номера.

Стрелки могут быть произвольной длины и направления, но обязательно располагаться слева на право. (по возможности избегать взаимного пересечения стрелок)

Приступая к составлению сети, необходимо установить, какие работы:

• должны быть завершены раньше, чем начнется данная (предшествующая работа);

• могут быть начаты после завершения данной;

• могут выполняться одновременно с данной работой.

При построении сети обязательно составляется черновой вариант.

Далее ее можно упорядочить. При этом в нее часто приходится добавлять так называемые «забытые» работы.

При построении сетевых графиков встречаются сложные комплексные связи. Например:

• две или более работ имеют общие начальные и конечные события.

Эти работы выполняются параллельно (совмещено), но продолжительность их разная.

Т.е. совмещение нужно изображать так, чтобы любая работа могла соединяться только с двумя событиями. В этом случае надо показать взаимосвязь работ, вводя дополнительное событие, и фиктивную работу.

рис.1

• для выполнения одной из работ, например (5,6) (рис.2) необходимо предварительно выполнить работы (2,5), (3,5), (4,5), а для другой (5,7) - выполнение только (4,5)

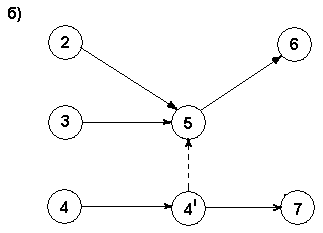
рис.2

В этом случае изображение а) – неверное, так как получается, что выполнение работы (5,7) зависит от (2,5), (3,5) и (4,5). Нужно: ввести в сеть дополнительное событие (4') и фиктивную работу (4',5) - б).

• чтобы отразить в проекте плана разработки время и место дополнительных материальных, финансовых и трудовых ресурсов, на сетевых графиках вводят так называемые подставки. Внешне подставки принято изображать двойным кружком с нулем (рис.3)

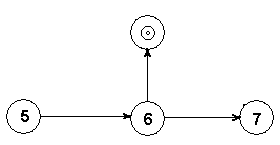
рис.3

Иногда изображаются орг.связи (пунктирные стрелки с полотнами – для отличия от фиктивных работ)

• двусторонние связи изображаются введением фиктивных работ.

Напр., пусть имеются 3 процесса А, В, С.

При этом окончание С зависит от результатов А и В. В данном случае возникают двусторонние зависимости (рис.4).

рис.4

• При построении сетевых графиков иногда бывает целесообразно укрупнить работы путем замены их совокупности данной «агрегатной», если какая-то группа имеет одно начальное и одно конечное событие (рис.5)

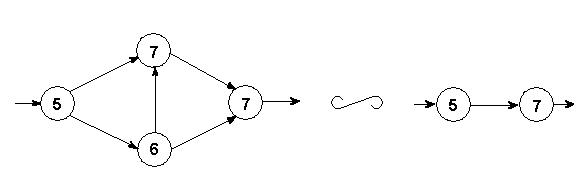
рис.5

При проверке правильности составления сети выясняют:

1. нет ли на графике работ, имеющих одинаковые кода. Если они есть, то следует ввести дополнительные события и фиктивные работы;

2. в сети не должно быть «тупиков», т.е. событий, из которых не выходит ни одна работа (кроме последнего);

3. в сети не должно быть событий (кроме начального), которым не предшествует хотя бы одна работа;

4. нельзя допускать, чтобы два смежных события были связаны двумя или большим количеством работ;

5. в сети не должно быть замкнутых контуров;

6. если какие-либо работы могут быть начаты до полного окончания непосредственно предшествующей им, то последняя должна быть отражена как ряд последовательно выполняемых работ, каждая из которых завершается определенным событием.

7. правильность изображения частично (дифференциально) зависимых работ.

В связи с делением сетевых графиков по степеням детализации при составлении сводных графиков возникает необходимость объединения (сшивания) частных в общую сеть. Процесс сшивания сетей сопровождается выявлением и ликвидацией несогласованностей, различных неувязок и упрощением локальных графиков.

Составление сетевых графиков ведется в 3 этапа:

I этап – формирование задания, определяющего конечную цель разработки. Кроме основной (конечной) цели, следует выделить и промежуточные, которые должны быть взаимосвязаны как по последовательности, так и по результатам достижения. Промежуточные цели, определяют уровень выполнения программы, и является частными задачами, которые нужно решить для достижения основной цели.

II этап – заключается в составлении структурной схемы разработки, или так наз. «дерева разработки», которые должны наглядно показывать объём и этапы работ.

Для составления структурной схемы программа делится на подсистемы, подсистемы – на комплексы, комплексы – на элементы.

III этап – составление перечня работ в каждом звене и формирование их временных оценок.