
- •7.1 Расчет, построение и анализ кривых окислительно – восстановительного
- •7.2 Индикаторы, применяемые в окислительно – восстановительном титровании
- •7.3 Краткая характеристика конкретных методов
- •7.2 Индикаторы, применяемые в окислительно – восстановительном
- •7.3 Краткая характеристика конкретных методов
- •Подробнее см Калинкин и.П. Титриметрические методы анализа. Примеры решения задач. Учебное пособие :[Текст] / и.П. Калинкин, т.Э. Маметнабиев - сПб.: сПбГти (ту), 2009. - 43 c.( №1578) – пример 42
- •Калинкин и.П. Титриметрические методы анализа. Примеры решения задач. Учебное пособие :[Текст] / и.П. Калинкин, т.Э. Маметнабиев - сПб.: сПбГти (ту), 2009. –
- •43 C.( №1578) – пример № 3 с.13,14.
И.П.Калинкин, Т.Э. Маметнабиев.
Лекция № 7
7.1 Расчет, построение и анализ кривых окислительно – восстановительного
титрования.
7.2 Индикаторы, применяемые в окислительно – восстановительном титровании
7.3 Краткая характеристика конкретных методов
окислительно ‑ восстановительного титрования.
Для подготовки к контрольной работе и к сдаче коллоквиума по окислительно – восстановительному титрованию необходима также тщательная проработка методических указаний и учебного пособия:
Калинкин И.П. Титриметрические методы анализа [Текст]: методические указания/ Калинкин И.П., Маметнабиев Т.Э. – СПб: СПбГТИ (ТУ), 2008 – 48с.
(№ 465).
Калинкин И.П. Титриметрические методы анализа. Примеры решения задач. Учебное пособие :[Текст] / И.П. Калинкин, Т.Э. Маметнабиев - СПб.: СПбГТИ (ТУ), 2009. – 43 c.( №1578).
7.1 В отличие
от кривых других видов титрования, в
которых кривые титрования обычно строят
в координатах
![]() кривые редоксметрического титрования,
как правило, строят в координатах
кривые редоксметрического титрования,
как правило, строят в координатах
![]() или
или
![]() .
.
Если в редокс ─ реакции участвуют компоненты следующих обратимых
редокспар:
 (7.1)
(7.1)
 (7.2)
(7.2)
и
![]() ,
то Ox1
выступает в качестве окислителя, который
взаимодействует с восстановителем
Red2.
Как Ox1,
так и Red2
могут быть либо определяемым веществом,
либо титрантом ( реагентом):
,
то Ox1
выступает в качестве окислителя, который
взаимодействует с восстановителем
Red2.
Как Ox1,
так и Red2
могут быть либо определяемым веществом,
либо титрантом ( реагентом):
определяемое
титрант вещество (аналит)
оксидиметрическое
титрование
![]() (7.3)
(7.3)
редуциметрическое
титрование
![]() (7.4)
(7.4)
После добавления
каждой порции титранта в растворе
устанавливается равновесие:
![]() =
=![]() и в случае обратимых редокспереходов:
и в случае обратимых редокспереходов:
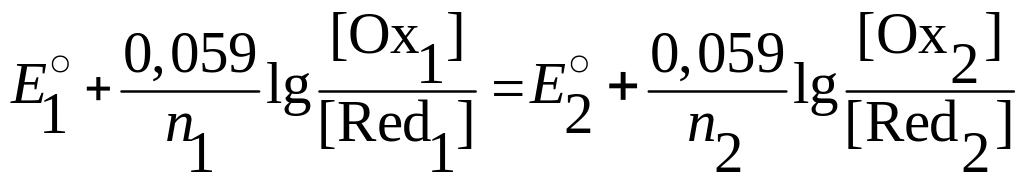 ,
(7.5))
,
(7.5))
Следовательно, для вычисления потенциала в любой точке кривой титрования, кроме начального момента, для которого отношение [Oxi] / [Redi] неизвестно, расчет можно вести по концентрациям компонентов либо первой, либо второй пары.
Расчет целесообразно
вести по той редокс ─ паре, которая
доминирует в процессе титрования при
соответствующем значении потенциала,
т.е. до точки эквивалентности в
интервале 0 < < 100 %,
расчет редокс ─ потенциала удобнее
вести по концентрациям компонентов той
пары, которая содержит определяемое
вещество; концентрация этого вещества
![]() ,
концентрация второго компонента этой
редокс ─ пары
,
концентрация второго компонента этой
редокс ─ пары
![]() .
.
После точки
эквивалентности (при > 100 %)
расчет лучше вести по второй паре,
содержащей титрант. После точки
эквивалентности титрант больше не
расходуется на химическое взаимодействие
с определяемым веществом. Происходит
лишь накапливание титранта и, следовательно,
его концентрацию можно вычислить по
формуле
![]() ,
где
,
где
![]() – доля избытка титранта. Концентрация
второго компонента этой редокспары
– доля избытка титранта. Концентрация
второго компонента этой редокспары
![]() .Потенциал
в точке эквивалентности рассчитывают
по формуле :
.Потенциал
в точке эквивалентности рассчитывают
по формуле :
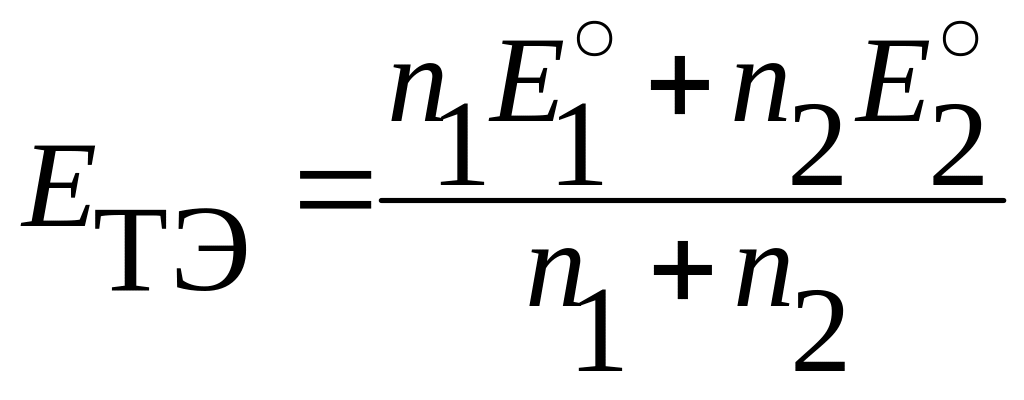 .
.
Вывод.
Потенциал в точке эквивалентности, согласно (7.5), можно выражать как потенциал первой пары и в то же время как потенциал второй пары:
![]() (7.6)
(7.6)
![]() (7.7)
(7.7)
После умножения левой и правой части уравнения (7.6) на n1, а уравнения (7.7) – на n2 и сложения получают:
![]() (7.8)
(7.8)
![]() (7.9)
(7.9)
Из условий стехиометрии вышеприведенных уравнений (7.3) и (7.4) в точке эквивалентности имеют место соотношения:
![]() (7.10)
(7.10)
Следовательно, под логарифмом в уравнении (7.9) стоит единица, сам логарифм равен нулю, и редокс ─ потенциал в точке эквивалентности можно вычислить по формуле:
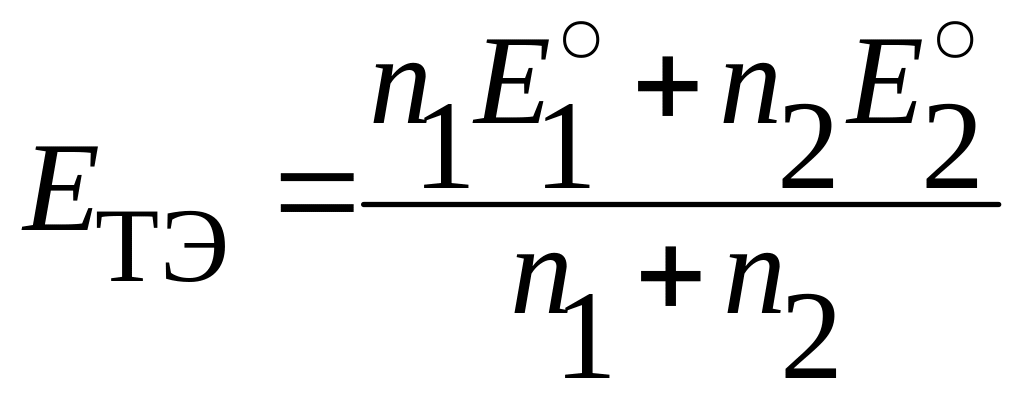 (7.11))
(7.11))
На основании изложенных положений расчет значений окислительно ─ ‑восстановительного потенциала при построении кривых редоксметрических титрований производится по следующим формулам:
При оксидиметрических титрованиях
Значения τ,% |
Расчетные уравнения |
0 <τ <100 |
|
50 |
|
100 |
|
> 100 |
|
200
|
|
При редуциметрических титрованиях.
Значения τ,% |
Расчетные уравнения |
0 < τ <100 |
|
50 |
|
100 |
|
τ >100 |
|
200
|
|
Следует помнить, что в более строгих и корректных расчетах во всех уравнениях вместо стандартных потенциалов следует подставлять условные (формальные)
окислительно ─ восстановительные потенциалы.
Общий вид кривых оксидиметрических титрований, построенных по результатам вычисления окислительно ─ восстановительного потенциала с помощью уравнений
(7.11), (7.12) и
(7.13) для случаев
![]() и
и
![]()
![]() представлен на рис. .
представлен на рис. .
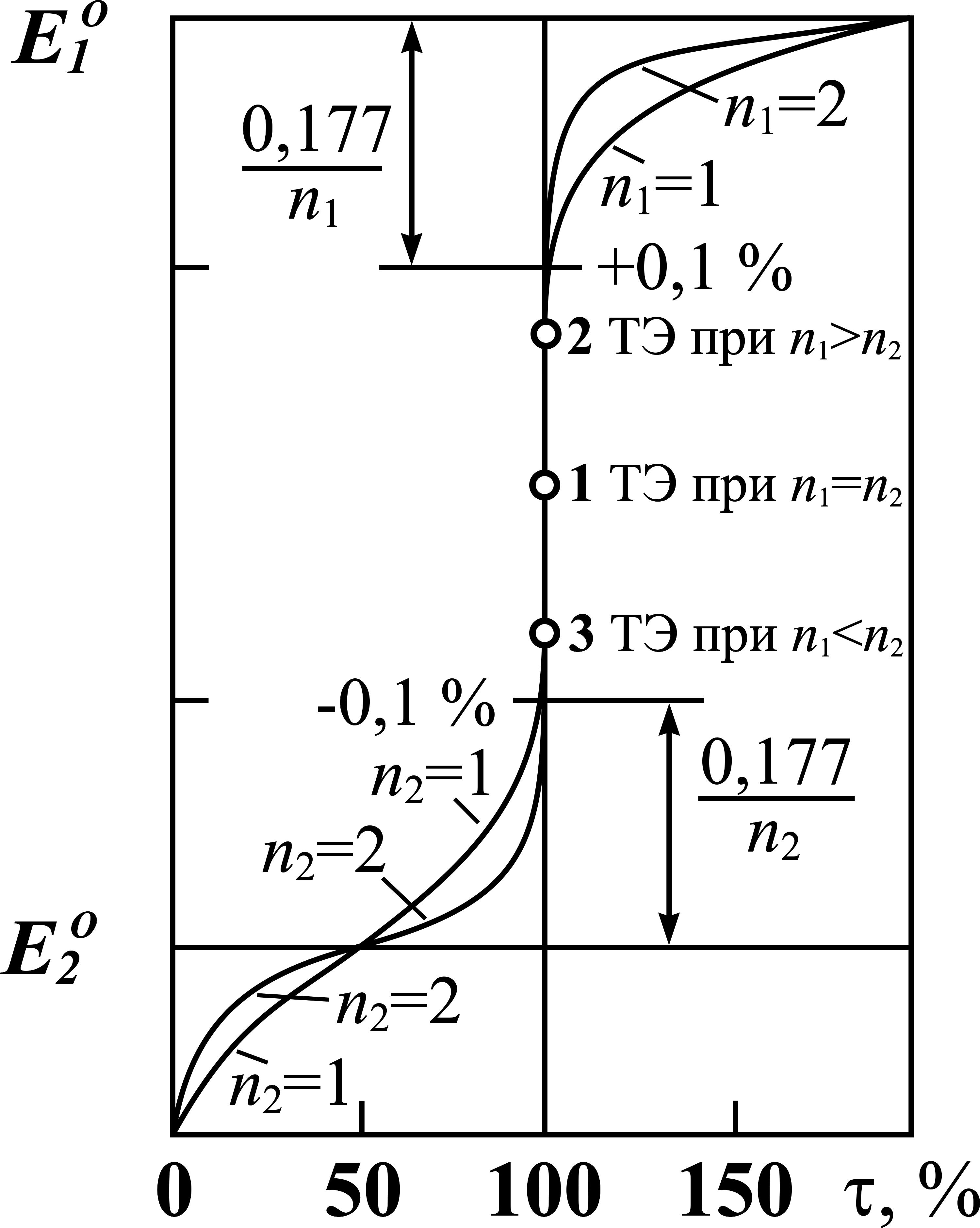
Рисунок. Кривые оксидиметрических титрований.
Рассмотрим и проанализируем теперь в качестве примера общий вид кривых оксидиметрических титрований. На рис. представлены кривые, построенные по результатам вычисления окислительно-восстановительного титрования с помощью формул
( 7.12 ) и ( 7.13 ) для
случаев
![]() и
и
![]()
![]() .
.
Характерными чертами кривых окислительно ‑ восстановительного титрования является то, что:
1) Концентрация титруемого раствора и титранта не влияет на кривые редоксметрических титрований, если только в процессе реакции титрования не изменяется число частиц, например, как в случае редокспары Cr2O72– + 14H+ → 2Cr3+ + 7H2O;
2) Точка эквивалентности находится в середине скачка кривой титрования только при n1 = n2. В противном случае точка эквивалентности смещена в сторону
одной из ветвей кривой титрования.
Величина скачка титрования определяется степенью оттитрованности (τ%) вблизи точки эквивалентности. Если реакция протекает количественно, то
при оксидиметрическом титровании, при τ% от 99,9% до 100,1% ((погрешность титрования 0,1%), согласно уравнению ( 7.12 ), скачок титрования начинается при:
![]()
а заканчивается , согласно уравнению ( 7.13 ), при:
![]()
Величина скачка титрования равна:
![]()
![]()
Отсюда
следует, что редоксметрические титрования
с погрешностью
![]() 0,1%
возможны если:
0,1%
возможны если:
![]() ( 7.16)
( 7.16)
Правая
сторона неравенства ( 7.16) имеет наибольшее
значение при n1=n2=1.
В этом случае должно быть
![]() .
Следовательно , если разность
стандартных потенциалов больше 0,35В,
то при любых значениях n1
и n2
редоксметрические титрования можно
выполнять не превышая погрешность
.
Следовательно , если разность
стандартных потенциалов больше 0,35В,
то при любых значениях n1
и n2
редоксметрические титрования можно
выполнять не превышая погрешность
![]() 0,1%.
Аналогично можно показать, что титрования
с погрешностью
1%,
когда τ%=99% и
101% возможны, если
0,1%.
Аналогично можно показать, что титрования
с погрешностью
1%,
когда τ%=99% и
101% возможны, если
![]() .
.
Теперь рассмотрим в качестве примера расчет реперных точек кривой редуциметрического титрования раствора Fe (III) стандартным раствором Sn (II). Для оценочного расчета примем 0,059 ≈ 0,06.
Согласно формулам (7.14) и (7.15) имеем:
![]() ;
;![]()
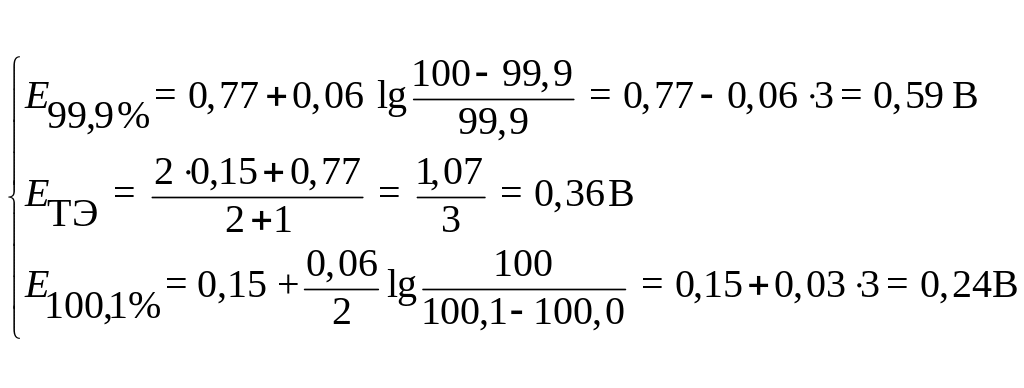
![]()
Вычисления по рассмотренным выше формулам приводят к данным, совпадающим с экспериментально наблюдаемыми потенциалами, только в случае термодинамически обратимых редокспар. Так, например, экспериментальная кривая перманганатометрического титрования ионов железа (II) не совпадает с вычисленной таким образом кривой. Кроме того, экспериментальные данные плохо воспроизводимы. В случае же бихроматометрического титрования ионов железа (II) экспериментальная и вычисленная кривые хорошо совпадают.

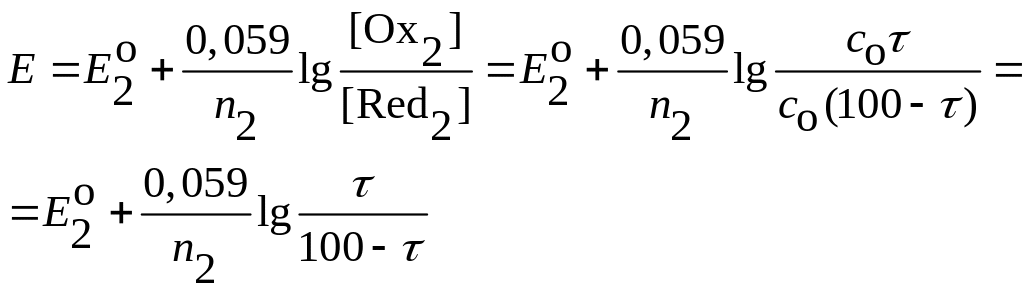 (7.12)
(7.12)
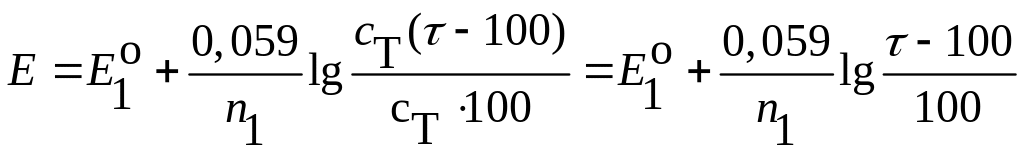 (7.13)
(7.13) (7.14)
(7.14) (7.15)
(7.15)