5. Третье начало термодинамики может быть сформулировано так:

«Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система». где x — любой термодинамический параметр.Третье начало термодинамики относится только к равновесным состояниям.Поскольку на основе второго начала термодинамики энтропию можно определить только с точностью до произвольной аддитивной постоянной (то есть, определяется не сама энтропия, а только её изменение): третье начало термодинамики может быть использовано для точного определения энтропии. При этом энтропию равновесной системы при абсолютном нуле температуры считают равной нулю.Третье начало термодинамики позволяет находить абсолютное значение энтропии, что нельзя сделать в рамках классической термодинамики (на основе первого и второго начал термодинамики). В классической термодинамике энтропия может быть определена лишь с точностью до произвольной аддитивной постоянной S₀, что не мешает термодинамическим исследованиям, так как реально измеряется разность энтропий (S₀) в различных состояниях. Согласно третьему началу термодинамики, при значение .

В качестве критерия самопроизвольности процес–сов в открытых и закрытых системах вводится новая функция состояния – энергия Гиббса. Эта функция получила название в честь великого американского физика Д. У. Гиббса (1839—1903), который вывел эту функцию, а затем использовал в термодинамических работах.

Энергия Гиббса определяется через энтальпию Н и энтропию S с помощью соотношений:G = H – S, ΔG = ΔH – ΔS.На основе энергии Гиббса второе начало термодина–мики можно сформулировать следующим образом: в изобарно-изотермических условиях (р, Т = const) в системе самопроизвольно могут осуществляться только такие процессы, в результате которых энер–гия Гиббса системы уменьшается (ΔG <0).В со–стоянии равновесия энергия Гиббса системы не ме–няется (G = const, AG = 0).ΔG < 0, р, Т = const.Из изложенного вытекает, что энергия Гиббса игра–ет большую роль в изучении биоэнергетических про–цессов. С помощью этой функции состояния можно прогнозировать направление самопроизвольных про–цессов в биологических системах и рассчитывать мак-сималь-но достижимый КПД.Энергия Гиббса G так же, как и энтальпия Н, являет–ся функцией состояния системы. Поэтому изменение энергии Гиббса ΔG может использоваться для харак–теристики химических превращений аналогично изме–нению энтальпии ΔН. Уравнения реакции, для которых указывается соответствующее этим реакциям изменение энергии Гиббса, также называются термо–химическими.Химические реакции, при протекании которых про–исходит уменьшение энергии Гиббса системы (ΔG < 0) и совершается работа, называются экзергоническими. Реакции, в результате которых энергия Гиббса возрас–тает (ΔG > 0) и над системой совершается работа, называются эндергоническими.

Выведенная на основе второго начала термодина–мики энергия Гиббса является функцией состояния. Следовательно, так же, как и для энтальпии, может быть сформулирован закон Гесса для энергии Гиббса в следующей форме: изменение энергии Гиббса при образовании заданных продуктов из данных реа–гентов при постоянных давлении и температуре не зависит от числа и вида реакций, в результате ко–торых образуются эти продукты.

6. Скорость химической реакции - это изменение концентрации реагирующих веществ в единицу времени.При гомогенных реакциях пространством реакции обозначается объем реакционного сосуда, а при гетерогенных - поверхность, на которой протекает реакция. Концентрацию реагирующих веществ обычно выражают в моль/л - количестве молей вещества в 1 литре раствора.Скорость химической реакции зависит от природы реагирующих веществ, концентрации, температуры, давления, поверхности соприкосновения веществ и ее характера, присутствия катализаторов. Увеличение концентрации веществ, вступающих в химическое взаимодействие, приводит к увеличению скорости химической реакции. Это происходит потому, что все химические реакции проходят между некоторым количеством реагирующих частицами (атомами, молекулами, ионами). Чем больше этих частичек в объеме реакционного пространства, тем чаще они соударяются и происходит химическое взаимодействие. Химическая реакция может протекать через один или несколько элементарных актов ( соударений). На основании уравнения реакции можно записать выражение зависимости скорости реакции от концентрации реагирующих веществ. Если в элементарном акте участвует лишь одна молекула (при реакции разложения), зависимость будет иметь такой вид: n = k*[A]Это уравнение мономолекулярной реакции. Когда в элементарном акте происходит взаимодействие двух разных молекул, зависимость имеет вид:n = k*[A]*[B]Реакция называется бимолекулярной. В случае соударения трех молекул справедливо выражение:n = k*[A]*[B]*[C] Реакция называется тримолекулярной. Обозначения коэффициентов:n - скорость реакции;[А], [В], [С] - концентрации реагирующих веществ; k - коэффициент пропорциональности; называется константой скорости реакции.

если реакция гетерогенная, то большую роль играет площадь поверхности соприкосновения веществ

моль/м² сек

 

Скорость гомогенной реакции измеряется изменением молярной концентрации (или изменением числа молей в единице объёма) одного из реагирующих веществ в единицу времени. Скорость гетерогенной реакции измеряется изменением числа молей одного из реагирующих веществ на единице площади соприкосновения в единицу времени.Скорость химической реакции — изменение количества вещества одного из реагирующих веществ за единицу времени в единице реакционного пространства. Является ключевым понятием химической кинетики. Скорость химической реакции — величина всегда положительная, поэтому, если она определяется по исходному веществу (концентрация которого убывает в процессе реакции), то полученное значение домножается на −1.

Например для реакции:

выражение для скорости будет выглядеть так:

.

7. ФОТОХИМИЧЕСКИЕ РЕАКЦИИ , хим. р-ции, протекающие под действием света. Поглощение фотона с длиной волны ~ 100-1500 нм, чему соответствует энергия 0,8-12,4 эВ (80-1200 кДж/моль), вызывает квантовый переход молекулы в-ва из основного электронного состояния в одно из возбужденных состояний или фотоионизацию - отщепление электрона и образование катион-радикала. Возбужденные состояния молекул имеют отличную от основного состояния электронную структуру и, как правило, более высокую реакционную способность. Молекулы вступают в хим. р-ции, первичные продукты к-рых (ионы, радикалы, изомеры) чаще всего оказываются нестабильными. Конечные продукты Ф. р. появляются в результате обычных термич. р-ций, к-рые протекают либо непосредственно с участием первичных частиц, либо как ряд последовательных хим. превращений.Как правило, для молекул с четным числом электронов при фотовозбуждении первоначально образуется возбужденное синглетное состояние (с мультиплетностъю , равной 1). Ф. р. обычно протекает из нижнего возбужденного синглетного состояния или из триплетного состояния (мультиплетность 3), к-рое получается из возбужденного синглетного состояния путем интеркомбинационной конверсии (изменения спина одного из электронов).С хим. р-циями возбужденных молекул конкурируют фо-тофиз. процессы: испускание фотона (флуоресценция или фосфоресценция), внутренняя и интеркомбинационная конверсия в нижележащие электронные состояния (триплетное или основное). Вследствие этих процессов времена жизни возбужденных синглетных состояний обычно не превышают 10^-8-10^-9с. Триплетные состояния в жидких р-рах обычно "гибнут" в результате безызлучат. перехода и дезактивации (тушения) примесями (напр., кислородом); времена их жизни не превышают 10^-5 с. В "жестких" средах (замороженных р-рах, полимерных матрицах), где процессы дезактивации замедляются, времена жизни триплетных состояний могут достигать десятка секунд. Фотохимические реакции — химические реакции, которые инициируются воздействием электромагнитных волн, в частности — светом. Примерами фотохимических реакций являются фотосинтез в растениях, распад бромида серебра в светочувствительном слое фотопластинки, превращение молекул кислорода в озон в верхних слоях атмосферы, фотоизомеризация, фотохимически инициируемые перициклические реакции, фотохимические перегруппировки (напр. ди-π-метановая перегруппировка) и т.п. Основными требованиями для фотохимических реакций являются:энергия источника излучения должна соответствовать энергии электронного перехода между орбиталями; излучение должно быть способным достичь целевых функциональных групп и не быть заблокированным реактором и другими функциональными группами. Фотовозбуждение — первая стадия фотохимического процесса, когда реагирующее вещество переходит в состояние с повышенной энергией. Фотосенсибилизатор поглощает излучение и передаёт энергию реагирующему веществу. Обратный процесс называется «закалкой», когда фотовозбуждённое состояние деактивируется химическим реагентом.Фотовозбуждение — это механизм возбуждения электронов путём поглощения фотона, при котором энергия фотона значительно ниже порога фотоионизации. Поглощение фотона происходит в соответствии с квантовой теорией Планка.Фотовозбуждение играет главенствующую роль в процессефотоизомеризации; кроме того, используется в цветосенсибилизированных солнечных батареях, фотохимии, люминисценции, лазерах с оптической накачкой и других фотохромных приложениях.

8. Растворами называются гомогенные системы переменного состава, в которых растворенное вещество находится в виде атомов, ионов или молекул, равномерно окруженных атомами, ионами или молекулами растворителя. Любой раствор состоит по меньшей мере из двух веществ, одно из которых считается растворителем, а другое - растворенным веществом. Растворителем считается компонент, агрегатное состояние которого такое же, как и агрегатное состояние раствора.Растворы могут существовать в газообразном, жидком или твердом агрегатном состоянии. Воздух, например, можно рассматривать как раствор кислорода и других газов в азоте; морская вода - это водный раствор различных солей в воде. Металлические сплавы относятся к твердым растворам одних металлов в других. Растворение веществ является следствием взаимодействия частиц растворяемого вещества и растворителя. В начальный момент времени растворение идет с большой скоростью, однако по мере увеличения количества растворенного вещества возрастает скорость обратного процесса - кристаллизации. Кристаллизацией называется выделение вещества из раствора и его осаждение.Для большинства твердых веществ растворимость в воде увеличивается с повышением температуры.Раствор, содержащий меньше растворенного вещества, чем насыщенный, называется ненасыщенным раствором.Способы выражения концентрации растворов.

1) Массовая доля раствора ω (х). Выражается отношением массы растворенного вещества m(х) к массе раствора. Является величиной безразмерной или выражается в процентах:

2) Молярная концентрация раствора С(х). Выражается отношением количества растворенного вещества n(x) к объему раствора, выраженному в литрах.

Мольная доля (N) – отношение числа молей данного компонента (n₁) к сумме молей данного компонента и всех других компонентов раствора (растворителя и других растворенных веществ (n₂):

Моляльная концентрация (В) в моль/кг – отношение количества растворенного вещества в молях (n) к массе растворителя (m):

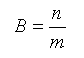Для характеристики состава раствора используются следующие способы выражения концентраций:

1) Массовая доля (w) – это доля, которую составляет масса растворенного вещества(m_в) от массы раствора

2) Массовая доля в процентах(w, %) – это выраженная в процентах доля, которую составляет масса растворенного вещества от массы раствора :

3) Молярная концентрация (С_м) – характеризует количество растворенного вещества(n_в) в одном литре раствора.4) Нормальная концентрация (C_n или N) – характеризует количество вещества эквивалента(n_э), содержащегося в 1 литре раствора:5) Моляльная концентрация (C_m) – характеризует количество растворенного вещества(n_в), содержащегося в 1000 г растворителя(m_р-ля) :6) Титр (Т) – характеризует массу вещества, содержащуюся в 1 мл раствора:

7) Мольная доля (X) – характеризует долю, которая составляет количество веществ всех компонентов раствора. Мольная доля – величина безразмерна

9. Представим, что в равновесную систему жидкость А – пар введено некоторое вещество В. При образовании раствора мольная доля растворителя X_А становится меньше единицы; равновесие в соответствии с принципом Ле Шателье – Брауна смещается в сторону конденсации вещества А, т.е. в сторону уменьшения давления насыщенного пара Р_А. Очевидно, что, чем меньше мольная доля компонента А в растворе, тем меньше парциальное давление его насыщенных паров над раствором. Для некоторых растворов выполняется следующая закономерность, называемая первым законом Рауля:

Парциальное давление насыщенного пара компонента раствора прямо пропорционально его мольной доле в растворе, причем коэффициент пропорциональности равен давлению насыщенного пара над чистым компонентом.

                         

Поскольку сумма мольных долей всех компонентов раствора равна единице, для бинарного раствора, состоящего из компонентов А и В легко получить следующее соотношение, также являющееся формулировкой первого закона Рауля:

                      

Относительное понижение давления пара растворителя над раствором равно мольной доле растворенного вещества и не зависит от природы растворенного вещества.

Растворы, для которых выполняется закон Рауля, называют идеальными растворами. Идеальными при любых концентрациях являются растворы, компоненты которых близки по физическим и химическим свойствам (оптические изомеры, гомологи и т.п.) и образование которых не сопровождается объёмными и тепловыми эффектами. В этом случае силы межмолекулярного взаимодействия между однородными и разнородными частицами примерно одинаковы, и образование раствора обусловлено лишь энтропийным фактором. Растворы, компоненты которых существенно различаются по физическим и химическим свойствам, подчиняются закону Рауля лишь в области бесконечно малых концентрациях.

10. КОНОВАЛОВА ЗАКOНЫ, связывают изменения состава равновесно сосуществующих жидкой и паровой фаз двойной системы с изменениями т-ры или давления. В совр. формулировке первый Коновалова закон устанавливает: при постоянной т-ре Т = const давление пара р-ра возрастает (уменьшается) при увеличении концентрации того компонента, содержание к-рого в паре больше (меньше), чем в р-ре; при постоянном давлении р = const т-ра кипения р-ра возрастает (уменьшается) при увеличении концентрации того компонента, содержание к-рого в паре меньше (больше), чем в р-ре. Второй Коновалова закон: в точке экстремума на кривой зависимости равновесного давления от состава р-ра (пара) при Т=const или на кривой концентрационной зависимости т-ры кипения (конденсации) при р=const составы сосуществующих в равновесии жидкости и пара совпадают. Экстремумы на кривых р(х)при Т=const и Т(х) при р=const (х-молярная доля одного из компонентов) наблюдаются при одинаковом составе; если давление имеет максимум, то т-ра - минимум, и наоборот. Третий Коновалова закон: при постоянных т-ре или давлении изменение составов жидкого р-ра и пара происходит в одном направлении (симбатно). Коновалова законы справедливы вдали от критического состояния рассматриваемой системы. Они теоретически обоснованы и экспериментально подтверждены для двойных систем, состоящих из жидкой и паровой фаз, Д. П. Коноваловым в 1881-84 независимо от Дж. Гиббса, к-рым в 1876-78 были высказаны более общие положения. Установлено (А. В. Сторонкин, А. Г. Морачевский, 1959), что при определенных способах изменения состава первый и третий Коновалова законы справедливы и для многокомпонентных систем. Второй Коновалова закон часто наз. законом Гиббса-Коновалова; он справедлив для систем с любым числом компонентов. Законы, аналогичные Коновалова законам, могут быть сформулированы применительно к равновесиям твердый р-р - пар и твердый р-р - жидкий р-р (для последних обычно рассматривают диаграммы состояния в координатах Т—х при р=const). Коновалова законы играют важную роль при построении диаграмм фазового равновесия, анализе эксперим. данных о равновесии жидкость - пар, разработке методов ректификац. разделения в-в.

11.Температура кристал. понижения температуры замерзания и повышения температуры кипения растворов, которые в объединённом виде известны как второй закон Рауля. Понижение температуры кристаллизации растворов.Условием кристаллизации является равенство давления насыщенного пара растворителя над раствором давлению пара над твёрдым растворителем. Поскольку давление пара растворителя над раствором всегда ниже, чем над чистым растворителем, это равенство всегда будет достигаться при температуре более низкой, чем температура замерзания растворителя.Разность между температурой кристаллизации растворителя T°_fr и температурой начала кристаллизации раствора T_fr есть понижение температуры кристаллизации.Понижение температуры кристаллизации бесконечно разбавленных растворов не зависит от природы растворённого вещества и прямо пропорционально моляльной концентрации раствора. Повышение т. Кип. Р-ов.Жидкость кипит при той температуре, при которой общее давление насыщенного пара становится равным внешнему давлению. Если растворённое вещество нелетуче (то есть давлением его насыщенных паров над раствором можно пренебречь), то общее давление насыщенного пара над раствором равно парциальному давлению паров растворителя.Таким образом, температура кипения раствора нелетучего вещества T_b всегда выше, чем температура кипения чистого растворителя при том же давлении T°_b.Повышение температуры кипения бесконечно разбавленных растворов нелетучих веществ не зависит от природы растворённого вещества и прямо пропорционально моляльной концентрации раствора

Температура кипения разбавленных растворовТемпература кипения растворов нелетучего вещества всегда выше, чем температура кипения чистого растворителя при том же давлении. Рассмотрим Р - T диаграмму состояния растворителя и растворов различной концентрации (рис.3.5). Любая жидкость - растворитель или раствор - кипит при той температуре, при которой давление насыщенного пара становится равным внешнему давлению. Соответственно температуры, при которых изобара Р = 1 атм. пересечет кривые ОА, ВС и DE, представляющие собой зависимости давления пара над чистым растворителем и растворами с возрастающими концентрациями соответственно, будут температурами кипения этих жидкостей

Повышение температуры кипения растворов нелетучих веществ ДT_к = T_к - T°_к пропорционально понижению давления насыщенного пара и, следовательно, прямо пропорционально моляльной концентрации раствора. Коэффициент пропорциональности E есть эбулиоскопическая постоянная растворителя, не зависящая от природы растворенного вещества.Т.о., второй закон Рауля можно в наиболее общем виде сформулировать следующим образом:Понижение температуры замерзания и повышение температуры кипения разбавленного раствора нелетучего вещества прямо пропорционально моляльной концентрации раствора и не зависит от природы растворенного вещества.Второй закон Рауля является следствием из первого; данный закон справедлив только для бесконечно разбавленных растворов. Коэффициенты пропорциональности в уравнениях (III.14 - III.15) - эбулиоскопическая и криоскопическая константы - имеют физический смысл соответственно повышения температуры кипения и понижения температуры замерзания растворов с моляльной концентрацией, равной 1 моль/кг. Однако, поскольку такие растворы не являются бесконечно разбавленными, эбулиоскопическая и криоскопическая константы не могут быть непосредственно определены и относятся поэтому к числу т.н. экстраполяционных констант.

12. Осмотическим давлением называется величина, измеряемая минимальным гидравлическим давле–нием, которое нужно приложить к раствору, чтобы осмос прекратился.

Законы осмотического давления.

Вант-Гофф предложил эмпирическое уравнение для расчета осмотического давления разбавленных раст–воров неэлектролитов:

π = С(Х)RT,

где π – осмотическое давление, кПа;

С(Х) – молярная концентрация, моль/л;

R – универсальная газовая постоянная, равная

8,31 кПа – л/(моль – К);

Т – абсолютная температура, К.

Хотя закон Вант—Гоффа был установлен на основе экспериментальных данных, он может быть выведен из условий термодинамического равновесия при ΔG = 0. Поэтому этот закон следует рассматривать как следст–вие второго начала термодинамики.

Выражение в вышеуказанной форме аналогично уравнению Клапейрона—Менделеева для идеальных газов, однако эти уравнения описывают разные про–цессы.

По Вант-Гоффу осмотическое давление раствора численно равно тому газовому давлению, которое имело бы растворенное вещество, будучи переведенным в газообразное состояние в том же объеме и при той же температуре. Поскольку объем (разбавление) обратно пропорционален концентрации, то закон Вант-Гоффа можно записать в виде

Правило Вант-Гоффа — эмпирическое правило, позволяющее в первом приближении оценить влияние температуры на скорость химической реакции в небольшом температурном интервале (обычно от 0 °C до 100 °C). Я. Х. Вант-Гофф на основании множества экспериментов сформулировал следующее правило:

При повышении температуры на каждые 10 градусов константа скорости гомогенной элементарной реакции увеличивается в два — четыре раза.

Уравнение, которое описывает это правило следующее:

где  — скорость реакции при температуре ,  — скорость реакции при температуре ,  — температурный коэффициент реакции (если он равен 2, например, то скорость реакции будет увеличиваться в 2 раза при повышении температуры на 10 градусов).

Следует помнить, что правило Вант-Гоффа применимо только для реакций с энергией активации 60-120 кДж/моль в температурном диапазоне 10-400^oC. Правилу Вант-Гоффа также не подчиняются реакции, в которых принимают участие громоздкие молекулы, например белки в биологических системах. Температурную зависимость скорости реакции более корректно описывает уравнение Аррениуса.

Из уравнения Вант-Гоффа температурный коэффициент вычисляется по формуле:

13.Эле.дис.Для объяснения особенностей водных растворов электролитов шведским ученым С.Аррениусом в 1887 г. была предложена теория электролитической диссоциации. В дальнейшем она была развита многими учеными на основе учения о строении атомов и химической связи. Современное содержание этой теории можно свести к следующим трем положениям:

1. Электролиты при растворении в воде распадаются (диссоциируют) на ионы - положительные и отрицательные.Ионы находятся в более устойчивых электронных состояниях, чем атомы. Они могут состоять из одного атома - это простые ионы (Na⁺, Mg²⁺, Аl³⁺ и т.д.) - или из нескольких атомов - это сложные ионы (NО₃^-, SO^2-₄, РО^З-₄и т.д.). 2.  Под действием  электрического  тока ионы  приобретают  направленное движение: положительно заряженные ионы движутся к катоду, отрицательно заряженные - к аноду. Поэтому первые называются катионами, вторые - анионами.3. Диссоциация - обратимый процесс: параллельно с распадом молекул на ионы (диссоциация) протекает процесс соединения ионов (ассоциация).Например, уравнение диссо­циации молекулы электролита КA на катион К⁺ и анион А^- в общем виде записывается так: КА   K⁺ + A Теория электролитической диссоциации является одной из основных теорий в неорганической химии и полностью согласуется сатомномолекулярным учением и теорией строения атома.Слабые электролиты.Вещества, частично диссоциирующие на ионы. Растворы слабых электролитов наряду с ионами содержат недиссоциированные молекулы. Слабые электролиты не могут дать большой концентрации ионов в растворе. К слабым электролитам относятся: 1) почти все органические кислоты (CH₃COOH, 2) некоторые неорганические кислоты (H₂CO₃₎ 3) почти все малорастворимые в воде соли, основания и гидроксид аммония (Ca₃(PO₄)₂; Cu(OH)₂;) 4) вода. Они плохо (или почти не проводят) электрический ток. Cu(OH)₂ « [CuOH]⁺ + OH^- (первая ступень) [CuOH]⁺ « Cu²⁺ + OH^- (вторая ступень) Константа диссоциации (K_D) - отношение произведения равновесных концентраций ионов в степени соответствующих стехиометрических коэффициентов к концентрации недиссоциированных молекул.Она является константой равновесия процесса электролитической диссоциации; характеризует способность вещества распадаться на ионы: чем выше K_D, тем больше концентрация ионов в растворе.Диссоциации слабых многоосновных кислот или многокислотных оснований протекают по ступеням, соответственно для каждой ступени существует своя константа диссоциации:

 Первая ступень:H₃PO₄  H⁺ + H₂PO₄^-; KD₁ = ([H⁺][H₂PO₄^-]) / [H₃PO₄] = 7,1 • 10^-3

 Вторая ступень:H₂PO₄^-  H⁺ + HPO₄^2-;KD₂ = ([H⁺][HPO₄^2-]) / [H₂PO₄^-] = 6,2 • 10^-8

 Третья ступень:HPO₄^2-  H⁺ + PO₄^3-;KD₃ = ([H⁺][PO₄^3-]) / [HPO₄^2-] = 5,0 • 10^-1

Закон разбавления Оствальда — соотношение, выражающее зависимость эквивалентной электропроводности разбавленного раствора бинарного слабого электролита от концентрации раствора: Здесь К — константа диссоциации электролита, с — концентрация, λ и λ_∞ — значения эквивалентной электропроводности соответственно при концентрации с и при бесконечном разбавлении. Соотношение является следствием закона действующих масс и равенства где α — степень диссоциации.Закон разбавления Оствальда выведен В.Оствальдом в 1888 и им же подтвержден опытным путём.

14. Сильные электролиты Это вещества, которые при растворении в воде практически полностью распадаются на ионы. Как правило, к сильным электролитам относятся вещества с ионными или сильно полярными связями: все хорошо растворимые соли, сильные кислоты (HCl, HBr, HI, HClO₄, H₂SO₄,HNO₃) и сильные основания (LiOH, NaOH, KOH, RbOH, CsOH, Ba(OH)₂,Sr(OH)₂,Ca(OH)₂). В растворе сильного электролита растворённое вещество находится в основном в виде ионов (катионов и анионов); недиссоциированные молекулы практически отсутствуют.

ДЕБАЯ - ХЮККЕЛЯ ТЕОРИЯ, статистич. теория разбавленных растворов сильных электролитов, позволяющая рассчитать коэффициент активности ионов. Основана на предположении о полной диссоциации электролита на ионы, которые распределены в растворителе, рассматриваемом как непрерывная среда. Каждый ион действием своего электрич. заряда поляризует окружение и образует вокруг себя некоторое преобладание ионов противоположного знака - так называемой ионную атмосферу. В отсутствие внешний электрич. поля ионная атмосфера имеет сферич. симметрию и ее заряд равен по величине и противоположен по знаку заряду создающего ее центральное иона. Потенциал  суммарного электрич. поля, создаваемого центральное ионом и его ионной атмосферой в точке, расположенной на расстоянии r от центральное иона, может быть рассчитан, если ионную атмосферу описывать непрерывным распределением плотности  заряда около центральное иона.