1.Передаточная функция объекта:

2.Передаточная функция ПИ-регулятора:

4.Оптимизируем отработку единичного скачка внутреннего возмущения: f₁(t)=1(t).

5.Критерий оптимальности:

при =0,95.

Надо определить параметры настройки ПИ-регулятора при внутреннем возмущении, удовлетворяющем критерию оптимальности.

Методика вывода формул для расчета параметров настройки ПИ-регулятора.

1.Запишем передаточную функцию замкнутой системы при скачкообразном внутреннем воздействии:

2.Запишем передаточную функцию объекта и регулятора в относительных единицах времени:

;

где r= p, T=T₁/, I_и=Т_и/.

3.Обозначим коэффициент усиления разомкнутой системы

К=к_р к_об;

Тогда

где , , ,

4.Воспользовавшись методикой Вышнеградского, изменим масштаб

, где

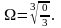
Тогда

где , ,

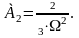
5.В диаграмме Вышнеградского требуется найти одну точку, которая бы удовлетворяла критерию оптимальности. Эта точка имеет координаты А₁=2,539, А₂=1,853.

6.Путем преобразований получаем рабочие формулы:

;

; ;

7.По значению относительной постоянной времени находим масштабные коэффициенты и определяем прямые показатели качества:

х_max=m_x k_об;

t_max=_max m_t ;

t_п=_п m_t .

ПУНКТ 3: МЧК для объектов без запаздывания с ограничением максимальной величины регулирующего воздействия.

Исходные данные те же.

Надо определить параметры настройки ПИ-регулятора при внутреннем возмущении, удовлетворяющем критерию оптимальности.

Методика вывода формул.

1.Запишем передаточную функцию замкнутой системы при скачкообразном внутреннем воздействии:

2.Запишем передаточную функцию замкнутой системы по задающему воздействию:

.

3. Запишем передаточную функцию как изменение [х_р]_доп от времени при скачкообразном внутреннем возмущении:

4.Для линейных САР последовательно соединенные звенья можно менять местами. Следовательно, ограничить максимальную величину регулирующего воздействия можно, так подобрав параметры оптимальной динамической настройки ПИ-регулятора, чтобы максимальная величина регулируемого параметра не превышала допустимой величины регулирующего воздействия.

5.Критерию оптимальности соответствуют следующие значения коэффициентов Вышнеградского: А₁=А₂=2. В результате рабочими формулами для расчета параметров настройки ПИ-регулятора являются:

; ;

; .

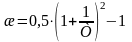6.По значению относительной постоянной времени находим масштабные коэффициенты и определяем прямые показатели качества:

х_max=m_x k_об;

t_max=_max m_t ;

t_п=_п m_t .

ММЧК для расчета параметров динамической настройки ПИ-регулятора и объекта с запаздыванием для отработки внутреннего возмущения.

Исходные данные:

1.Передаточная функция объекта:

2.Передаточная функция ПИ-регулятора:

3.Структурная схема:

4.Оптимизируем отработку единичного скачка внутреннего возмущения: f₁(t)=1(t).

5.Критерий оптимальности:

при =0,9.

Надо определить параметры настройки ПИ-регулятора при внутреннем возмущении, удовлетворяющем критерию оптимальности.

Получены следующие аналитические зависимости параметров настройки ПИ-регулятора в функции относительной постоянной времени объекта Т:

относительный коэффициент усиления

относительное время интегрирования

,

где относительная постоянная времени объекта

время интегрирования регулятора ,

коэффициент усиления регулятора

По численному значению Т находим нормированную кривую оптимального переходного процесса при отработке f₁. С помощью графика зависимости масштабного коэффициента от Т переходим к абсолютным единицам.