1.Передаточная функция объекта:

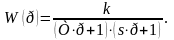
2.Передаточная функция ПИ-регулятора:

3.Структурная схема:

y

-1

4.Оптимизируем отработку скачка задания: х_зд(t)=1(t).

5.Критерий оптимальности:

, При степени затухания Ψ=0,95

Рассчитать параметры оптимальной динамической настройки ПИ-регулятора.

Алгоритм решения задачи:

1.Находим передаточную функцию замкнутой САР по задающему воздействию

(1);

2.Находим передаточную функцию разомкнутой системы с учетом, что Т_и=Т₁

(2);

3.Подставим (2) в (1) и после преобразований получим формулы для расчета параметров оптимальной динамической настройки ПИ-регулятора

Т_и=Т_к;

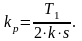
4.Прямые показатели качества:

Величина перерегулирования х_max=4,3 %.

Время первого достижения регулируемой величиной заданного значения t₁=4,7 .

Полное время регулирования t_п=6,3 .

МПК с учетом ограничений на максимальную величину регулирующего воздействия для объектов без запаздывания.

Исходные данные те же.

Постановка задачи:

по заданной передаточной функции объекта с ПИ-регулятором одноконтурной САР надо так подобрать параметры настройки ПИ-регулятора, чтобы величина максимального регулирующего воздействия не превышала допустимое значение.

Порядок определения оптимального коэффициента усиления регулятора k_р следующий:

1.по заданной величине [х_р]_доп и отношению Т₁/ определяем соответствующее значение коэффициента ;

2.по найденному значению коэффициента  и отношению Т₁/ находим по графику относительный коэффициент усиления К;

3.оптимальное значение коэффициента усиления регулятора вычисляем по формуле

k_p=K/k_об;

4.оптимальное значение времени интегрирования регулятора находим из условия Т_и=Т₁.

5.по численному значению  находим нормированную кривую оптимального переходного процесса и определяем прямые показатели качества.

Классификация и сущность методов полной компенсации для оптимизации внешних возмущений (см. 11 и 12 все целиком).

Существует три МПК:

1)МПК в ЧВ для объектов без запаздывания и ПИ-регулятора, где в качестве критерия оптимальности колебательное звено с =1/2

2)МПК в ОВ для объектов с большим , где в качестве КО принято инерционное звено 1-го порядка с , при этом время разгона интегрального звена 1-го порядка Т_зд принимается чаще всего равным запаздыванию объекта и при этом условие ПИД регулятора отрабатывает 95% скачка задания за полное время Т_полн =4.

3)ММПК для объектов с большим , где в качестве КО принято кол. Звено с =1/2, сдвинутое вправо на _об.

Во всех трех методах время интегрирования Т_и=Т₁  большей постоянной времени объекта, т.е. опережающее действие времени действие регулятора полностью компенсирует Т₁ и поэтому оптимизированных ПП при отработке скачка задания зависят только от малой постоянной времени объекта  или _усл объекта, например для МПК и объекта передаточной функции ПИ регулятора настройка которого определена Т_и=Т₁;

к_р=Т₁/2к_об, оптимальный ПП:

W_Х,Хзд(р)=1/(1+2р+2²р²)

При этом прямые показатели качества будут: Т_полн, Т₁, Х_макс.

4)МПК с ограничением.

Классификация и сущность МЧК для оптимизации внутренних возмущений.

Если главным для системы регулирования является внутреннее возмущение, то настройку САР следует производить по следующим классификациям МЧК:

1)МЧК для объектов без запаздывания.

2)МЧК с ограничением для объектов без запаздывания.

3) МЧК для объектов с запаздыванием с ограничением (х=1,45).

4)ММЧК для объектов с запаздыванием.

пункт 1: МЧК для объектов без запаздывания.

Исходные данные: