46.Мпк в общем виде.

МПК в общем виде.

Исходные данные:

1.Передаточная функция объекта:

2.Структурная схема:

3

.Структурная схема:

y

-1

3.Оптимизируем отработку скачка задания: х_зд(t)=1(t).

4.Критерий оптимальности:

Время разгона экспоненты выбираем так, чтобы скорость изменения регулируемого параметра не превышала заданного значения. Обычно Т_зд=_зд.

Требуется определить для конкретной передаточной функции объекта структуру типового регулятора и так рассчитать параметры его динамической настройки, чтобы при отработке скачка задания регулируемая величина соответствовала критерию оптимальности.

Решение задачи:

Из структурной схемы находим передаточную функцию регулятора:

После подстановки W_об и W_х,хзд получим:

Для устранения передаточной функции звена чистого запаздывания решаем это уравнение графическим путем. В результате получаем:

Формула после подстановки конкретных значений Т_зд и W_об позволяет получить структуру регулятора, а затем формулы для расчета его параметров настройки.

Если , то получим ПИД-регулятор:

При малом значении  время дифференцирования получается малым, им можно пренебречь и ПИД-регулятор превращается в ПИ-регулятор.

47.Мпк в частном виде.

Расчет настройки корректирующего регулятора (по МПК в ЧВ)

• Находим абсолютное значение времени интегрирования:

• Для расчета коэффициента усиления регулятора запишем передаточную функцию заданной САР по задающему воздействию через передаточную функцию разомкнутой САР

Распишем передаточную функцию разомкнутой САР, как

Примем = ,

Передаточную функцию (3)разделим на числитель и подставим в (1):

Передаточную функцию (4) приравниваем к колебательному звену с коэффициентом демпфирования :

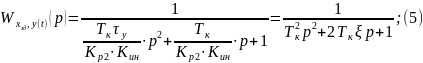
Приравниваем коэффициенты при p и и получаем систему из двух уравнений:

Решаем систему и получаем выражение для коэффициента усиления регулятора:

• Записываем передаточную функцию корректирующего регулятора:

Метод полной компенсации в частном виде для настройки ПИ-регулятора

МПК в частном виде для объектов с запаздыванием.

Исходные данные:

1.Передаточная функция объекта:

2.Передаточная функция ПИ-регулятора:

3.Структурная схема:

y

-1

4.Оптимизируем отработку скачка задания: х_зд(t)=1(t).

5.Критерий оптимальности:

, При степени затухания Ψ=0,95

Рассчитать параметры оптимальной динамической настройки ПИ-регулятора.

Алгоритм решения задачи:

1.Находим передаточную функцию замкнутой САР по задающему воздействию

(1);

2.Находим передаточную функцию разомкнутой системы с учетом, что Т_и=Т_к

(2);

3.Подставим (2) в (1) и после преобразований получим формулы для расчета параметров оптимальной динамической настройки ПИ-регулятора

Т_и=Т_к;

4.Прямые показатели качества:

Величина перерегулирования х_max=4,3 %.

Время первого достижения регулируемой величиной заданного значения t₁=3,8 _у.

Полное время регулирования t_п=6,1 _у.

МПК с учетом ограничений на максимальную величину регулирующего воздействия для объектов с запаздыванием.

Исходные данные те же.

Постановка задачи:

по заданной передаточной функции объекта с ПИ-регулятором одноконтурной САР надо так подобрать параметры настройки ПИ-регулятора, чтобы величина максимального регулирующего воздействия не превышала допустимое значение.

Порядок определения оптимального коэффициента усиления регулятора k_р следующий:

1.по заданной величине [х_р]_доп и отношению Т_к/_у определяем соответствующее значение коэффициента демпфирования ;

2.по найденному значению коэффициента демпфирования  и отношению Т_к/_у находим по графику относительный коэффициент усиления К;

3.оптимальное значение коэффициента усиления регулятора вычисляем по формуле

k_p=K/k_об;

4.оптимальное значение времени интегрирования регулятора находим из условия Т_и=Т_к.

5.по численному значению  находим нормированную кривую оптимального переходного процесса и определяем прямые показатели качества.

МПК в частном виде для объектов без запаздывания.

Исходные данные: