Типовые динамические звенья.

§ 1. Типовые динамические звенья.

1. Определение типового динамического звена.

В системах автоматического управления и регулирования применяется большое количество элементов, номенклатура которых насчитывает сотни, а для сложных систем и тысячи наименований. Несмотря на это, математическое описание элементов имеет гораздо меньший диапазон и насчитывает достаточно малое число видов дифференциальных уравнений.

Это обусловлено однотипностью динамических свойств (а значит и однотипностью математического описания) элементов, различающихся назначением, принципом действия, конструкцией и другими характеристиками.

Все это позволило ввести в теории автоматического регулирования и управления понятие типового динамического звена.

Под типовым динамическим звеном понимается звено однонаправленного действия, которое описывается дифференциальным уравнением не выше второго порядка (имеет передаточную функцию первого или второго порядка).

Под однонаправленностью понимается свойство звена пропускать сигнал только в одном направлении - от входа к выходу.

2. Классификация типовых динамических звеньев.

Динамические звенья классифицируются по виду левой и правой частей их дифференциального уравнения и состоят из трех групп: позиционные, интегрирующие и дифференцирующие.

Каждая из групп, в свою очередь, содержит по несколько типовых звеньев.

Рассмотрим наиболее часто встречающиеся типовые динамические звенья.

Обозначим входную величину звена через , а выходную через (рис. 1). Возмущение, действующее на звено, обозначим через .

Рис. 1. Схема динамического звена.

Статическая характеристика любого звена может быть изображена линией (рис. 1), т.к. рассматриваются линейные или, точнее, линеаризованные системы.

звеньях позиционного или статического типа линейной зависимостью в установившемся режиме связаны выходная и входная величины (рис. 2, а). Коэффициент пропорциональности между выходной и входной величинами представляет собой коэффициент передачи звена.

В звеньях интегрирующего типа линейной зависимостью связаны производная выходной величины и входная величина (рис. 2, б).

В этом случае для установившегося режима будет справедливо равенство , откуда и произошло название звеньев. Коэффициент пропорциональности также является коэффициентом передачи звена. Если входная и выходная величины звена имеют одинаковую размерность, то коэффициенту передачи соответствует размерность [с^-1].

Рис. 2. Типы линейных зависимостей динамических звеньев.

В звеньях дифференцирующего типа линейной зависимостью связаны выходная величина и производная входной (рис. 2, в). Коэффициент пропорциональности является коэффициентом передачи звена. Если входная и выходная величины имеют одинаковую размерность, то коэффициенту передачи соответствует размерность [с].

§ 2. Основные характеристики типового динамического звена.

1. Передаточные функции типовых динамических звеньев.

Классификация звеньев, как уже отмечалось, производится по виду дифференциального уравнения или, что одно и то же, по виду передаточной функции звена.

Предположим, что звено, изображенное на рис. 1, описывается дифференциальным уравнением, представленным в стандартной форме:

...(1).

При нулевых начальных условиях ( при ) и при отсутствии внешнего возмущения ( ) передаточная функция звена может быть найдена, как отношение изображений по Лапласу выходной и входной величин:

…(2).

При известной передаточной функции изображение выходной величины находится из выражения .

Аналогичным образом может быть найдена передаточная функция звена по возмущению, если положить, что при нулевых начальных условиях равно нулю входное воздействие :

…(3).

В таблице 1.1 приведены передаточные функции десяти типовых динамических звеньев.

Таблица 1.1. Типовые динамические звенья.

№п.п	Тип звена		Передаточная функция
1.	Позиционные	Безынерционное ;
2.		Апериодическое 1-го порядка ;
3.		Апериодическое 2-го порядка ;
4		Колебательное ;	, , ,
5.		Консервативное ;	,
6.	Интегрирующие	Идеальное интегрирующее ;
7.		Интегрирующее с замедлением ;
8.		Изодромное ;
9.	Дифференцирующие	Идеальное дифференцирующее ;
10.		Дифференцирующее с замедлением ;

2. Временные характеристики типовых динамических звеньев.

Динамические свойства звена могут быть определены по его переходной функции и функции веса.

2.1. Переходная функция или переходная характеристика представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равной единице (рис. 3).

Такое входное воздействие называется единичной ступенчатой функцией, которая равна: .

Предполагается, что единица имеет ту же размерность, что и физическая величина на входе звена.

Если входное воздействие представляет собой неединичную ступенчатую функцию , выходная величина будет равна .

Более строго переходную функцию звена можно определить как отношение выходной величины звена к высоте ступенчатого скачка на его входе, т.е. . При этом размерность соответствует размерности передаточной функции звена.

Умножение какой либо функции на единичную ступенчатую функцию означает, что функция времени будет существовать только при , при она обращается в ноль (рис. 4).

Рис. 3. Рис. 4. Рис. 5.

2.2. Функция веса w(t) представляет собой реакцию звена на единичную импульсную функцию, поданную на его вход (рис. 5).

Единичная импульсная функция, или дельта-функция, представляет собой производную от единичной ступенчатой функции: . Дельта-функция тождественно равна нулю повсюду, кроме точки , где она стремится в бесконечность.

Основное свойство дельта-функции заключается в том, что …(4), т.е. имеет единичную площадь.

Из последнего выражения следует, что размерность единичной дельта функции равна [с^-1]. Дельта-функция может быть представлена как предел некоторого выражения, например: .

Можно показать, что функция веса получается дифференцированием по времени переходной функции.

В случае, когда на вход звена поступает неединичная импульсная функция , на выходе звена получится .

Более строго функцию веса можно определить как отношение выходной величины звена к площади поданного на его вход импульса , т.е. . При этом размерность соответствует размерности передаточной функции звена, деленной на время.

Функция веса звена связана с его передаточной функцией преобразованием Лапласа, а именно: передаточная функция есть изображение функции веса и определяется интегральным соотношением ...(5).

В свою очередь, переходная функция звена связана с его передаточной функцией интегральным соотношением ...(6), т.е. имеет место интегральное преобразование Карсона.

Для входного воздействия произвольного типа, прикладываемого в момент времени , переходный процесс на выходе звена при нулевых начальных условиях м.б. определен на основании интеграла Дюамеля - Карсона по его переходной функции:

…(7),

или по функции веса:

…(8), где – вспомогательная переменная интегрирования, изменяющееся в пределах от нуля до рассматриваемого текущего момента времени .

3. Частотные характеристики динамических звеньев.

3.1. Частотная передаточная функция динамического звена.

Важнейшей характеристикой динамического звена является его частотная передаточная функция.

Для получения ее рассмотрим динамическое звено (рис. 1) в случае, когда возмущение , а на его входе имеется гармоническое воздействие , где - амплитуда, а – угловая частота этого воздействия.

На выходе линейного звена в установившемся режиме будет также гармоническая функция той же частоты, но в общем случае сдвинутая по фазе относительно входной величины на угол .

Таким образом, для выходной величины можно записать .

Воспользуемся формулой Эйлера представления тригонометрических функций на комплексной плоскости, и представим входную и выходную величины в виде суммы экспоненциальных функций с мнимым показателем:

…(9).

Здесь - мнимая единица.

В линейной системе на основании принципа суперпозиции можно рассмотреть отдельно прохождение составляющих . Кроме того, можно легко показать, что достаточно рассмотреть прохождение только составляющей , которая в выходной величине дает составляющую . Соотношение между составляющими получается такими же, как между .

Поэтому в дальнейшем рассмотрении воспользуемся символической записью . Тогда: …(10).

Символичность этой записи заключается в отбрасывании составляющих с множителем .

Для нахождения соотношения между входной и выходной гармоническими величинами звена воспользуемся его дифференциальным уравнением в виде, полагая :

…(11).

Из выражения (10) определим производные

.

Подставив значение входной и выходной величин и их производных в исходное дифференциальное уравнение, получим:

После сокращения на общий множитель найдем:

…(12).

Выражение (12) называется частотной передаточной функцией звена.

Таким образом, частотная передаточная функция 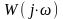представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент – сдвигу фаз выходной величины по отношению к входной:

…(13).

В более общей формулировке, для входного сигнала любого вида частотную передаточную функцию можно представить как отношение изображений Фурье (частотных изображений) выходной и входной величин: …(14), что непосредственно вытекает при переходе от изображения Лапласа к изображению Фурье.

Следовательно, частотная передаточная функция легко получается из обычной передаточной функции подстановкой .

Частотная передаточная функция звена есть изображение Фурье её функции веса, т.е. имеет место интегральной преобразование

...(15).

3.2. Частотные характеристики динамического звена.

Частотная передаточная функция, как любое комплексное число, может быть представлена в следующем виде:

…(16), где - модуль частотной передаточной функции, - аргумент или фаза, и - соответственно вещественная и мнимые составляющие частотной передаточной функции.

Для рассмотренного выше уравнения (11) модуль частотной передаточной функции находится как отношение модулей числителя и знаменателя выражения (12):

...(17).

Аргумент или фаза частотной передаточной функции находится как разность аргументов числителя и знаменателя выражения (12):

…(18).

Для нахождения вещественной и мнимой частей частной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части.

Для уравнения (11) и ее частотной передаточной функции (12) имеем:

…(19), ...(20).

Для наглядного представления частотных свойств динамического звена используются так называемые частотные характеристики.

3.2.1. Амплитудно-фазовая частотная характеристика (афх) строится на комплексной плоскости.

Она представляет собой геометрическое место концов векторов (годографов), соответствующих частотной передаточной функции , при изменении частоты от нуля до бесконечности (рис. 6).

Рис. 6. Пример амплитудно-фазовой частотной характеристики (афх).

По оси абсцисс откладывается вещественная часть и по оси ординат – мнимая часть . Для каждой частоты на комплексной плоскости наносится точка. Полученные точки соединяются затем плавной кривой. Около нанесенных точек можно написать соответствующие им частоты и т.д.

Афх может быть построена как для положительных, так и для отрицательных частот. При замене в частотной передаточной функции на получится сопряженная комплексная величина.

Поэтому афх для отрицательных частот строится как зеркальное изображение относительно вещественной оси афх для положительных частот.

На рисунке 6 афх для отрицательных частот показана пунктирной линией.

Положительные и отрицательные частоты имеют определенный смысл, т.к. они соответствуют положительным и отрицательным угловым скоростям вращения векторов на комплексной плоскости. В принципе можно ограничиваться рассмотрением только положительных частот. Однако при использовании всего диапазона частот от до многие формулы получают более удобный и симметричный вид.

Длина вектора, проведенного из начала координат в точку афх, соответствующую какой-либо выбранной частоте, равна модулю частотной передаточной функции.

Угол между вектором и положительным направлением вещественной оси, отсчитываемый против часовой стрелки, равен аргументу или фазе частотной передаточной функции.

Т.о., афх дает возможность наглядно представить для каждой частоты входного воздействия звена отношение амплитуд выходной и входной величин и сдвиг фаз между ними.

Построение афх по вещественной и мнимым частям частотной передаточной функции, как правило, является трудоемкой работой, т.к. умножение частотной передаточной функции на комплексную величину, сопряженную ее знаменателю, повышает в два раза степень частоты в знаменателе.

Обычно, гораздо проще строить афх, используя полярные координаты, т.е. вычисляя непосредственно модуль и фазу.

Зная модуль и фазу, можно легко построить соответствующую точку на комплексной плоскости. В случае необходимости при известном модуле и фазе легко вычислить вещественную и мнимую части умножением модуля на направляющий косинус между вектором и соответствующей осью.

3.2.2. Вместо афх можно построить отдельно амплитудную частотную характеристику (ачх) и фазовую частотную характеристику (фчх). Это построение проиллюстрировано на рисунках 7, а, б.

Ачх показывает, как динамическое звено пропускает сигнал различной частоты. Оценка пропускания определяется отношением амплитуд выходной и входной величин.

Фчх показывает фазовые сдвиги, вносимые звеном на различных частотах.

Для рассматриваемого типового динамического звена второго порядка модуль частотной передаточной функции представляет собой четную функцию частоты, а фаза – нечетную функцию частоты.

Поэтому по результатам вычисления модуля и фазы для положительных частот можно сразу построить ачх и фчх для всего диапазона частот .

Можно построить также отдельно вещественную и мнимую частотные характеристики по функциям и .

Это построение показано на рис. 8 а,б. И как сказано выше, вещественная характеристика представляет собой четную функцию частоты, а мнимая характеристика – нечетную функцию частоты.

Рис. 7, а. Амплитудная частотная характеристика (ачх).

Рис. 7, б. Фазовая частотная характеристика (фчх).

Рис. 8, а. Действительная часть афх.

Рис. 8, б. Мнимая часть афх.

3.3. Логарифмические частотные характеристики.

В ряде случаев оказывается полезным для количественной характеристики некоторых физических явлений вводить т.н. логарифмические величины.

Логарифмической называют величину, равную логарифму безразмерного отношения физической величины к однородной величине, принятую за исходную. К логарифмическим величинам относятся, например, уровень звукового давления, уровень громкости, усиление и ослабление электрической величины (напряженности электрического поля, напряжения, силы тока и т.п.).

Логарифмические величины выражаются во внесистемных логарифмических единицах – белах (децибелах) и неперах.

3.3.1. Логарифмическая амплитудная и логарифмическая фазовая частотная характеристики.

Прологарифмируем выражение частотной передаточной функции (16) : …(21).

Как видно из этого выражения, логарифм частотной передаточной функции равен комплексному выражению, вещественной частью которого является логарифм модуля, а мнимой – фаза.

Для практических целей удобнее пользоваться десятичными логарифмами и строить отдельно логарифмическую амплитудную частотную характеристику (лах) и логарифмическую фазовую частотную характеристику (лфх).

Для построения лах находится величина …(22).

Для построения лах используется стандартная сетка.

По оси абсцисс откладывается угловая частота в логарифмическом масштабе, т.е. наносятся отметки, соответствующие , а около отметок пишется само значение частоты в 1/с. Для этой цели может использоваться специальная полулогарифмическая бумага.

По оси ординат откладывается значение лах (22) в децибелах (дБ). Для этой цели на ней наносится равномерный масштаб.

Ось абсцисс должна проходить через точку 0 дБ, что соответствует значению модуля , т.к. логарифм единицы равен нулю.

Так как точка лежит на оси частот слева в бесконечности ( ), ось ординат может пересекать ось абсцисс (ось частот) в произвольном месте. Обычно ось ординат проводят таким образом, чтобы справа от нее можно было бы показать весь ход лах.

Для построения лфх используется та же ось абсцисс (ось частот).

По оси ординат откладывается фаза в градусах в линейном масштабе. Для практических расчетов удобно совместить точку нуля децибел с точкой, где фаза равна (–180 º). Отрицательный сдвиг по фазе откладывается по оси ординат вверх, а положительный – вниз.

Иногда по оси ординат указывается не сама частота, а ее десятичный логарифм (рис. 9). Единица приращения логарифма соответствует одной декаде, т.е. удесятирению частоты.

Применяется также деление частоты на октавы. Одна октава соответствует удвоению частоты.

Так как , то одна октава соответствует 0,303 декады.

Главным достоинством лах является возможность построения их во многих случаях практически без вычислительной работы. Это особенно проявляется в тех случаях, когда частотная передаточная функция может быть представлена в виде произведений сомножителей. Тогда результирующая лах находится суммированием ординат лах, соответствующих отдельным сомножителям.

Рис. 9.

Подводя итог рассмотренным в параграфе материалам, перечислим девять основных характеристик, которые полностью характеризуют динамические свойства типового динамического звена:

- передаточная функция;

- переходная функция или переходная характеристика;

- функция веса;

- частотная передаточная функция;

- амплитудно-фазовая частотная характеристика;

- амплитудная частотная характеристика;

- фазовая частотная характеристика;

- логарифмическая амплитудная частотная характеристика;

- логарифмическая фазовая частотная характеристика.