Часть1.Шпоры.Фпм

1.биномиальное распределение вероятностей используется в молекулярной физике для вычисления вероятности макросостояния системы, состоящей из большого числа частиц, а также для определения связи между равновесными и наиболее вероятными ее состояниями. Кроме того, на основе биномиального распределения можно получить математическую зависимость относительной флуктуации от числа частиц в системе. Кроме того, существует глубокая аналогия между моделью идеального газа и распределением плотности вероятности Гаусса для случайных непрерывных величин. Используя это распределение, можно вывести закон Максвелла для распределения молекул по скоростям и по энергиям. Например: Итак, пусть опыт повторяется n раз. Вероятность того, что из n опытов орел выпадет k раз (то есть событие А произойдет k раз), определяется биномиальным законом распределения:

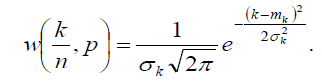
Биномиальное распределение справедливо при выполнении следующих условий:1, число испытаний n фиксировано 2, исход каждого опыта не зависит от результата других испытаний (независимые элементарные события) 3, вероятность p события А не зависит от номера опыта, т.е. p = const; 4, вероятность q того, что событие А не произойдет, равна q =1-p. Совокупность этих условий называется математической моделью биноминального эксперимента.

2. что означают понятия "дискретная" и "непрырывные величины".В теории вероятностей различают дискретные и непрерывные случайные величины. Дискретной называется случайная величина, принимающая конечное, или счетное, число значений. Это может быть некоторый набор чисел или функция, принимающая дискретные значения. Непрерывной называется случайная величина, принимающая непрерывное множество значений(вспомните понятие непрерывности в математическом анализе). Например, случайная величина k в формуле (1) является дискретной, а результат многократных измерений некоторой физической величины a (это может быть, например, ускорение, характерный размер тела, коэффициент температуропроводности и т.д.) является непрерывной случайной величиной, так как при измерениях могут получиться любые значения внутри некоторого интервала.

3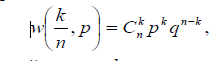 .Чем отличаются бином распред-ие от распред-ия гаусса? о:Отличия биноминального распределения от распределении гаусса в том, что что в распределении гаусса для большего числа вероятности того или иного случая надобно кол-во событии n или m стремящееся к бесконечности, т.е nПри переходе nбиноминальный закон распределения переходит в распределение лапласса-гаусса. Короче говоря

е сть формула биноминального распределении где фигурирует дискретная случайная величина k

а в распределении фигурирует непрерывная случайная величина х

4.Где в физике используется биноминальное распределение? короче вот ответ: Так, например, биномиальное распределение вероятностей используется в молекулярной физике для вычисления вероятности макросостояния системы, состоящей из большого числа частиц, а также для определения связи между равновесными и наиболее вероятными ее состояниями. Кроме того, на основе биномиального распределения можно получить математическую зависимость относительной флуктуации от числа частиц в системе. Используя распределение Гаусса , непосредственно в молекулярной физике а также в разделах физики, где изучаются явления беспорядочного движения и взаимодействия частиц(например: квантовая физика, атомная, ядерная и др.) (12), можно получить формулу для распределения молекул идеального газа по их скоростям и кинетическим энергиям - так называемое распределение Максвелла.

5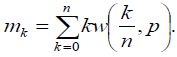 .Дайте определение математического ожидания и дисперсия случайной величины: Математическое ожидание определяется следующим образом: это среднее арифметическое случайной величины, найденное с учетом вероятностей. Математически оно определяется формулой:

Д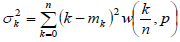 исперсией же называют среднее квадратов отклонений случайной величины от своего математического ожидания с учетом вероятности:

6 .Чему равно математическое ожидание и дисперсия случайной величины подчиняющейся биномиальному распределнию биномиальному распределению? о: Математическое ожидание определяется следующим образом: это среднее арифметическое случайной величины, найденное с учетом вероятностей. Для биномиального распределения оно равно: Математическое ожидание числа появлений события  в  независимых испытаниях равно произведению числа испытаний на вероятность появления события  в каждом испытании. Короче говоря: математическое ожидание для биномиального распределения равна

Дисперсия числа появлений события  в  независимых испытаниях равна произведению числа испытаний на вероятности появления и непоявления

с обытия  в одном испытании, иначе говоря Дисперсия характеризует "разброс" величины около ее среднего значения. Для биномиального распределения

 

7.Для чего необходимо в Лаб работе номер 1 каждый раз встряхивать кружку? Целью встряхивания кружки каждый раз перед подбрасыванием является достижение условии для биномиального распределения, иначе говоря, бином распределние диктует, что 1)число испытаний n фиксировано; 2)исход каждого опыта не зависит от результата других испытаний (независимые элементарные события); 3)вероятность p события А не зависит от номера опыта, т.е. p = const;

8.В чем причины расхождения результатов эксперимента с теоретическим распределением вероятности в "Лабораторной работе №1"?? Лабораторная работа №1 где Экспериментально проверяется биномиальное распределения и сравнение его с распределением Лапласа-Гаусса и распределением Гаусса, проверяется вероятность выпадения орла. Как же проверить, что вероятность выпадения, например, орла равна 1/2? Очевидно, необходимо провести n опытов, из которых в 50% случаев должен выпасть орел, а в 50% - решка. На практике при небольшом n это может не выполняться, то есть, например, из 10 бросаний не обязательно 5 раз выпадет орел, а 5 раз - решка. Однако в 100опытах эта закономерность выполнится точнее, в 1000 еще точнее и т.д. Абсолютно точно это распределение (50х50) выполнится при n®¥. Однако на практике мы можем провести только конечное число опытов. Поэтому возникает вопрос, какова вероятность того, что из n опытов n/2 раз выпадет орел? В более общем случае можно определить вероятности того, что из n опытов орел выпадет 0,1,2,3,…,k,…,n раз.

Причинами расхождения результатов эксперимента с теоретическим расхождением в том, что при проведении опыта, необходимо встряхивать кружку(монеты) , и при встряхивании каждые монеты воздействуют на друг на друга, и, в дальнейшем, на весь эксперимент и его результаты, иначе говоря монеты соударяясь друг с другом, влияют на результат каждого опыта.