Vybraná posloupnost

• Nechť (k_n) je rostoucí posloupnost přirozených čísel (indexů). Pak posloupnost (a_kn) se nazývá vybraná posloupnost z posloupnosti (a_n)

Zobecněná reálná čísla

• Množina R*= R sjednoceno (-∞, +∞) se nazývá rozšířená číselná osa, prvky množiny R* se nazývají zobecněná reálná čísla, prvky +,- ∞ jsou tzv. nevlastní body.

Na množině R* nejsou definovány tyto operace:

• +∞ - ∞

• 0 * (±∞)

• 

• a/ 0 kde a ϵ R*

Okolí vlastního bodu

• Otevřený interval ( a – Ɛ, a + Ɛ), kde Ɛ > 0, se nazývá okolí bodu a ϵ R

• Interval ( λ, +∞), kde λ ϵ R, se nazývá okolí bodu +∞

• Interval ( -∞, λ), kde λ ϵ R, se nazývá okolí bodu -∞

Limita posloupnosti

• Říkáme, že posloupnost (a_n) má limitu a ϵ R*, jestliže v každém okolí bodu a leží všechny členy posloupnosti a_n od jistého indexu n₀ počínaje

• Věta o jednoznačnosti limity

• Každá posloupnost má nejvýše jednu limitu.

• Věta o limitě konstantní posloupnosti

• Je-li (a_n) konstantní posloupnost, tj. a_n= a pro n ϵ N, pak existuje lim a_n a platí: lim a_n= a

• Věta o vybrané posloupnosti

• Jestliže posloupnost (a_n) má limitu, pak každá posloupnost z ní má vybraná má tutéž limitu

• Věta o limitě sevřené posloupnosti

• Nechť (a_n), (b_n), (c_n) jsou reálné posloupnosti. Jestliže od jistého indexu n₀ počínaje a_n < b_n < c_n a lim a_n = lim c_n, pak existuje lim b_n a platí: lim b_n =lim a_n = lim c_n

• Nechť (a_n) a (b_n) jsou reálné posloupnosti. Pak platí:

• lim (a_n± b_n) = lim a_n ± lim b_n

• lim (a_n * b_n) = lim a_n * lim b_n

• lim a_n/b_n = lim a_n / lim b

Spojitost funkce

• N echť funkce f je definována v okolí bodu c. Říkáme, že funkce f je spojitá v bodě c, jestliže pro každou posloupnost (x_n) obsaženou v D(f) platí: když x_n c, pak f (x_n) f(c)

Jednostranná spojitost

• Vyšetřujeme-li spojitost funkce f v bodě c, ale omezíme se při tom pouze na argumenty x v určitém buď levém, nebo pravém okolí bodu c, hovoříme o jednostranné spojitosti.

Vztah mezi jednostrannou a oboustrannou spojitostí

• Funkce f je spojitá v bodě c, právě když je v bodě c spojitá zprava i zleva.

Spojitost v intervalu

• Říkáme, že funkce f je spojitá v intervalu J, jestliže je spojitá ve všech vnitřních bodech intervalu J a v krajních bodech (pokud patří do intervalu) je spojitá zprava, resp. zleva

Spojitost elementárních funkcí

• Každá elementární funkce je spojitá v libovolném intervalu, na kterém je definována.

Bolzanova věta

• Je-li funkce f spojitá v intervalu <a,b> a f(a) * f(b) < 0, pak existuje c ϵ (a,b) takové, že f(c) =0

Weierstrassova věta

• Funkce spojitá v uzavřeném intervalu <a,b> má v tomto intervalu maximum i minimum.

Limita funkce

• Nechť funkce f je definována v prstencovém okolí bodu c ϵ R*. Říkáme, že funkce f má v bodě c limitu a ϵ R*, jestliže pro každou posloupnost (x_n) obsaženou v D (f) - {c} platí:

• k dyž x_n c, pak f (x_n) a

• Skutečnost, že funkce f má v bodě c limitu a značíme:

Jednostranná limita

• Limita zleva či zprava v bodě c. (analogicky jako jednostrannou spojitost)

Věta o vztahu jednostranných limit a oboustranné limity

• Limita funkce f v bodě c ϵ R existuje právě když existují obě jednostranné limity funkce f v bodě c a jsou si rovny. Pak platí

Věta o vztahu spojitosti a limity funkce

• Funkce f je v bodě c spojitá, právě když = f(c)

Věta o jednoznačnosti limity funkce

• Funkce f má v bodě c nejvýše jednu limitu

Věta o limitě operací pro funkce

• Nechť f a g jsou funkce jedné proměnné. Pak platí (limity kde x jde k c)

• lim (f(x) ± g(x)) = lim f(x) ± lim g(x)

• lim (f(x) * g(x)) = lim f(x) * lim g(x)

• lim f(x) / g(x) = lim f(x) / lim g(x)

pokud existují lim f(x), lim g(x) a operace na pravé straně vztahů jsou definovány.

Věta o limitě sevřené funkce

• Nechť f, g, h jsou funkce jedné proměnné, c ϵ R*. Jestliže v prstencovém okolí bodu c je f(x) ≤ g(x) ≤ h(x) a 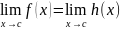pak existuje lim g(x) a platí:

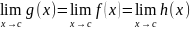
Věta o neurčitém limitním typu

• Jestliže 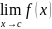je typu 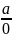, kde a≠0 a funkce f je v prstencovém okolí bodu c kladná pak resp. záporná pak

Věta o limitě složené funkce

• Nechť 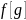je složená funkce z vnější funkce f a vnitřní g. Jestliže a vnější funkce f má v bodě d limitu, pak

DERIVACE

Derivace funkce v bodě c

• Nechť funkce f je definována v okolí bodu c. Číslo f´(c), definované vztahem f´(c) =

• Derivace funkce v bodě c je vlastní, když je funkce f spojitá v bodě c.

• Výsledkem vlastní derivace je reálné číslo

Geometrická interpretace f´(c)

• Derivace funkce f v bodě c je rovna směrnici tečny grafu funkce f v bodě 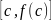, tj. f´(c) = tg α, kde α je úhel, který svírá tato tečna s kladnou poloosou x

Derivace zleva a zprava

• - derivace zprava

• - derivace zleva

Věta o vztahu jednostranné a oboustranné derivace

• Derivace funkce f v bodě c existuje právě když existují obě jednostranné derivace funkce f v bodě c a jsou si rovny. Pak platí f´(c) = f´₊(c) = f´_-(c)

Věta o vztahu derivace a spojitosti funkce

• Má-li funkce f v bodě c derivaci, pak je v bodě c spojitá. Obráceně to nemusí platit.

Derivace funkce f

• Funkce f´, definovaná předpisem

• Věta o derivaci základních funkcí

• Derivujeme podle vzorců, která platí ve všech bodech, pro které, mají výrazy smysl, tedy všude, kde existuje vlastní derivace dané funkce.

• Věta o derivaci operací a superpozice

• (f ± g)´= f´ ± g´

• (f * g)´= f´*g + f * g´

• (f / g)´ =

• (f(g))´= f´(g) * g´

Druhá derivace funkce f

• Funkce f´´, definovaná vztahem f´´=(f´)´

L’Hospitalovo pravidlo

• Limita podílu, která je neurčitého limitního typu se vypočítá jako limita podílu derivací čitatele a jmenovatele.

• Jestliže limita podílu funkcí lim f(x) /g(x) je typu „0/0“ nebo „∞/∞“ pak lim f(x) /g(x) = lim f´(x) / g´(x) pokud limita na pravé straně vztahu existuje (lim kde x jde do c)