Закон збереження заряда.

Отримане рівняння нерозривності тісно пов'язана з законом збереження заряду і по суті є його диференціальною формою.

Закон збереження заряду: Всякій зміні електричного заряду (q) всередині об'єму V, обмеженому поверхнею S, відповідає електричний струм, що втікає або випливає з цього об'єму:

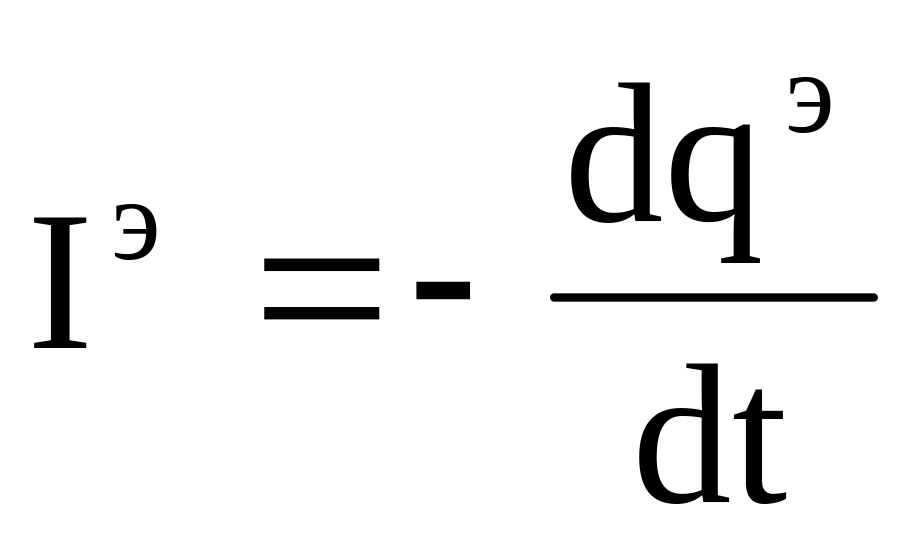(1).

Для того, щоб довести взаємозв'язок рівняння нерозривності і закону збереження повного струму, отримаємо закон збереження повного струму з рівняння нерозривності. Проінтегруємо рівняння нерозривності по об'єму:

.

Ліву частину перетворимо по теоремі Остроградського - Гаусса, а в правої частини поміняємо інтегрування з диференціюванням: .

Тут: , а .

Звідси отримуємо: .

49. Хвильові рівняння електродинаміки.

Для аналізу поширюються ЕМХ з системи рівнянь Максвелла в диференціальній формі доцільно виділити рівняння, які залежать або тільки від , або тільки від . При виведенні будемо вважати, що параметри середовища (, , ) не залежать від координат і часу.

Візьмемо ротор від :

. (1)

Після перетворення лівої частини і правої частини:

. (2)

Після перетворень отримаємо:

. (3)

Ми врахували наступне співвідношення для швидкості світла у вакуумі:

. (4)

. (5)

Рівняння (3) і (5) називають хвильовими рівняннями Ж. Д'Аламбера . Якщо права частина дорівнює нулю, то рівняння називають однорідним, а якщо ні - неоднорідним. При відсутності електричних зарядів ( = 0) рівняння (3) і (5) практично збігаються, що підтверджує рівноправність векторів і що поширюються в просторі ЕМП.

Незважаючи на гадану незалежність (6.3) і (6.5) слід пам'ятати про те, що у змінного ЕМП вектори і пов'язані і не можуть існувати одне без одного (випливає з (3.7) - (3.10)).

Хвильові рівняння в комплексній формі виводяться з рівнянь Максвелла в комплексній формі.

, (6)

, (7)

где – хвильове число: . (8)

Рівняння (6)-(7) називають хвильовими рівняннями Г. Гельмгольца [1-5].

У разі відсутності втрат провідності ( = 0) зникає другий доданок в (3) і (5), а також в (6) - (8) можливо спрощення – .

При відсутності магнітних втрат .

При наявності сторонніх джерел ЕМП або наявності залежності параметрів середовища від координат ліва частина рівняння не змінюється, але в правій частині з'являються додаткові складові.

Наприклад, якщо провідність середовища залежить від координат ((x, y, z)), то її не можна виносити за в (1), а слід виконати перетворення.

У результаті (3) запишеться у вигляді:

. (9)

Для вакуума (=0, ==1) рівняння Д’Аламбера (6.3) спрощується :

. (10)

Для отримується аналогічне рівняння (в (10) замінюється на ).

Розглянуті рівняння називаються хвильовими тому, що їх рішеннями є хвилі, і, зокрема, - ЕМХ (хвильові рівняння виду (10) у фізиці були отримані задовго до виявлення ЕМХ).

Як показали розрахунки та експерименти, «довільна» у фізичних аналогах (6.10) константа с для ЕМП дивним чином збігається із значенням швидкості світла у вакуумі. З цього був зроблений висновок про те, що ЕМХ і світло мають одну і ту ж природу. Як буде показано нижче, у просторі без втрат ЕМХ поширюються зі швидкістю світла.

Отримані хвильові рівняння відносяться до класу диференціальних рівнянь другого порядку в приватних похідних гіперболічного типу. Для довільної форми хвилі та довільної систему координат хвильові рівняння вирішити дуже важко, оскільки вид рішення і методи його отримання залежать від початкових умов і т. п.