47. Основні рівняння електромагнітного поля, їх фізичний зміст.

Третє рівняння Максвелла.

Третє рівняння Максвелла є узагальненням закону Гаусса на випадок змінних процесів. Потік вектора електричної індукції через поверхню S, обмежену об'ємом V дорівнює електричному заряду зосередженого усередині об'єму V:

.

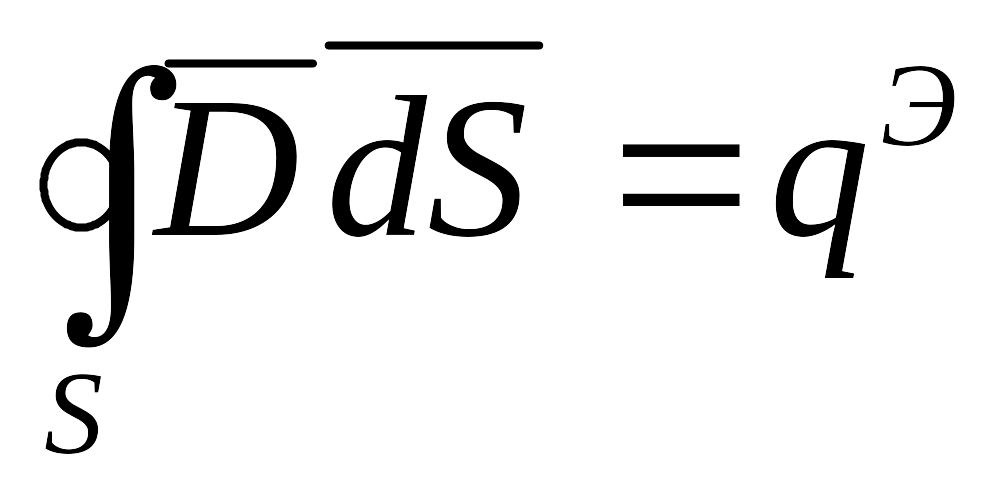Враховуючи, що отримаємо .

Останнє співвідношення справедливо, якщо рівні підінтегральні співвідношення. Звідси отримуємо: (1).

Отримане співвідношення і є третім рівнянням Максвелла.

Розгорнемо дивергенцію в системі координат: .

Аналізуючи (1) зазначимо, що витоками або стоками вектора електричного зміщення є вільні електричні заряди. Силові лінії починаються на позитивних зарядах і закінчуються на негативних. На відміну від вектора електричного зміщення витоками і стоками іншого електричного вектора - вектора напруженості можуть бути як вільні, так і пов'язані електричні заряди.

(2).

Підставим (2) в (1): (3).

Густина поляризаційних зарядів: (4).

Причиною виникнення цієї величини є нерівномірність речовини під дією зовнішнього електричного поля. Підставляючи (4) в (3), отримаємо: (5).

Четверте рівняння Максвелла.

Так як в природі не виявлено магнітних зарядів і струмів, то закон Гаусса та його диференційна форма в цьому випадку описуються наступним чином:

.

Векторне поле магнітної індукції не має стоків і витоків. Силові лінії замкнуті. Поле соленоідальне.

Перше рівняння Максвелла.

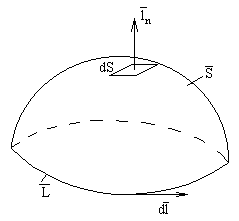
У середовищі з постійним струмом, який характеризується вектором об'ємної щільності , виділимо деякий замкнутий контур V і поверхня S, яка спирається на цей контур. Введемо позитивну одиничну нормаль до поверхні S.

Для того, щоб визначити поле вектора необхідно скористатися законом Ампера або законом повного струму.

Позитивний напрямок обходу контуру і одиничної нормалі пов'язані правилом правого гвинта. Напруженість магнітного поля можна визначити, використовуючи закон повного струму:

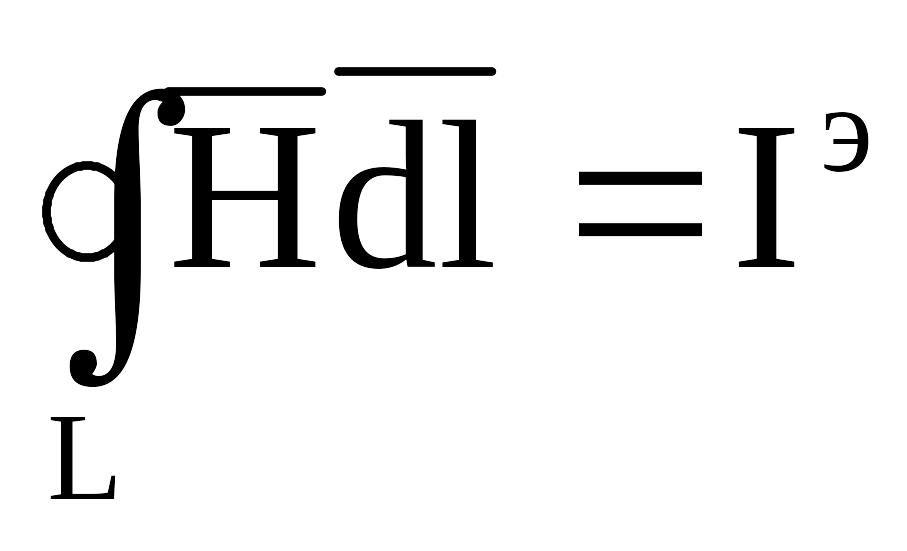(1).

Запишемо праву частину в інтегральній формі:

(2).

Ліву частину перетворимо по теоремі Стокса (поверхня S довільна):

.

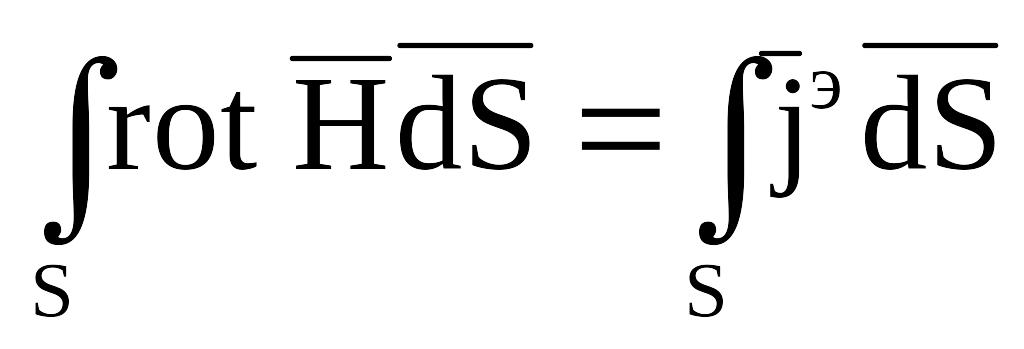(3)

Співвідношення (3) називається диференціальною формою закону повного струму для стаціонарного процесу. Візьмемо дивергенцію лівої і правої частин :

(4).

Будемо розглядати випадок змінного (нестаціонарний процес) струму. Повинно виконуватися співвідношення: 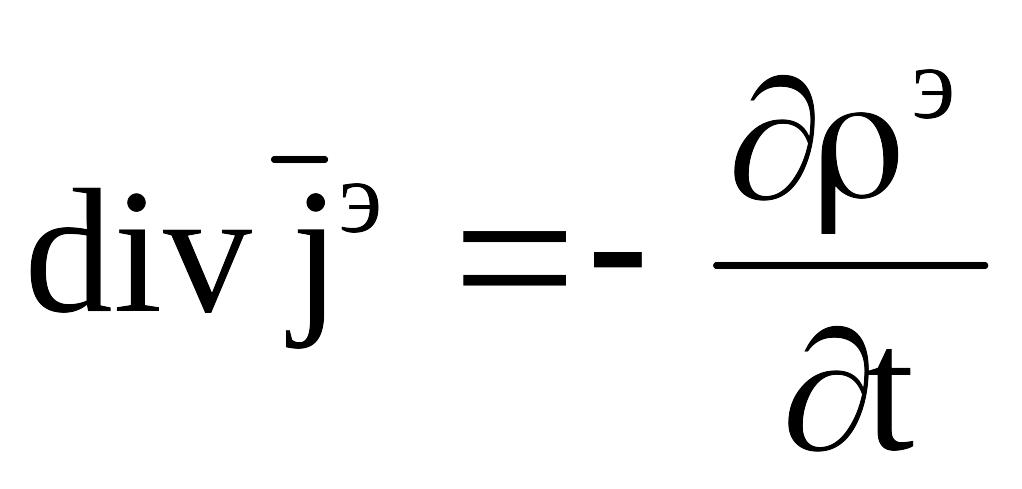. Однак виконувалося співвідношення (4). Максвелл додав деяку величину  і отримав: ; (4').

Використовуючи рівняння безперервності, він отримав: .

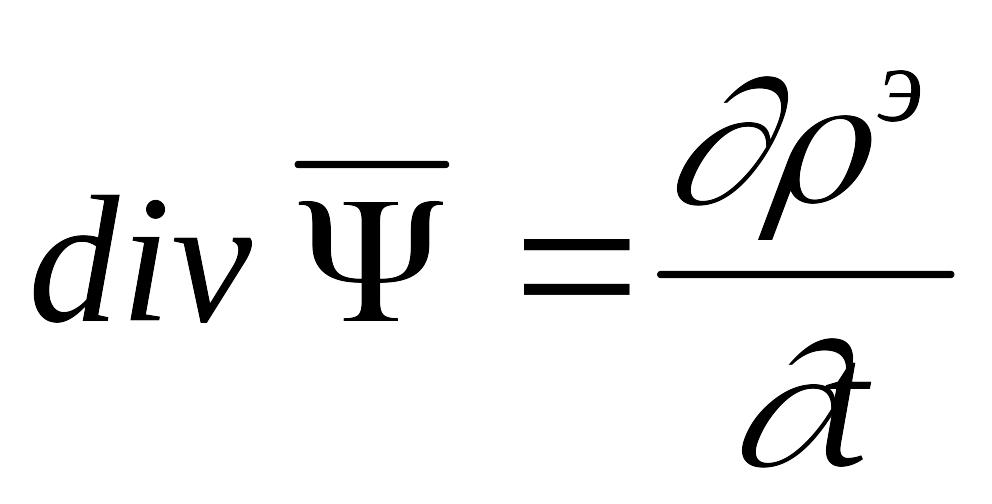Далі він скористався своїм третім рівнянням, тобто він приписав: .

Вважаємо, що функція та її похідна неперервні в кожній точці простору. В останньому співвідношенні поміняємо диференціювання у просторі та диференціювання за часом: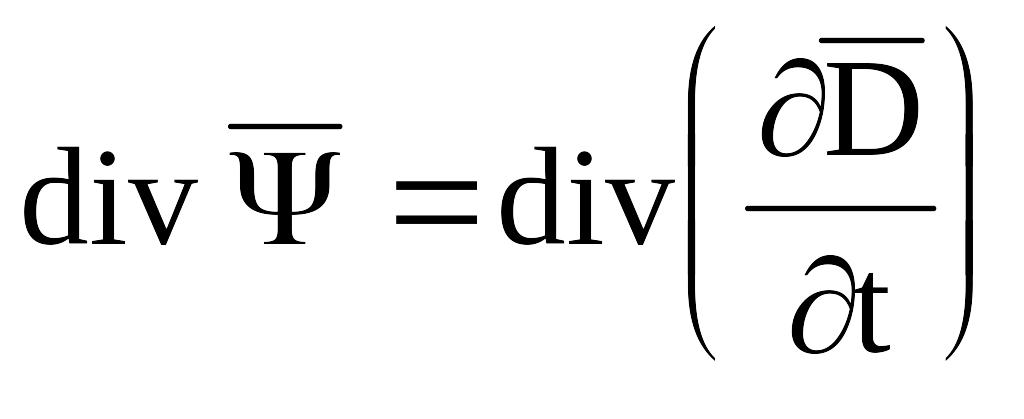

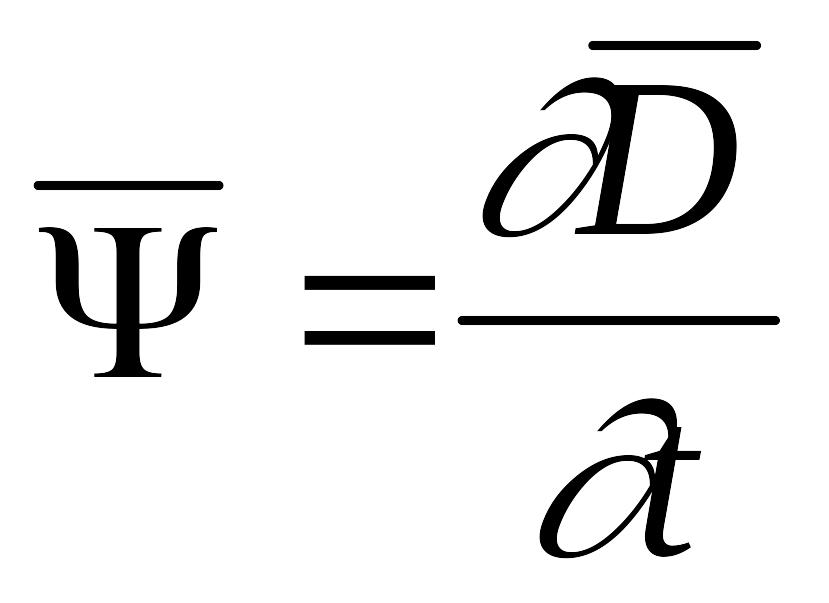(5)

Підставляємо (5) в (4'), отримаємо: (6).

Вираз (6) є диференціальною формою закону повного струму для нестаціонарного процесу. Доданок має сенс об'ємної щільності електричного струму. Вектор об'ємної щільності струму зміщення:

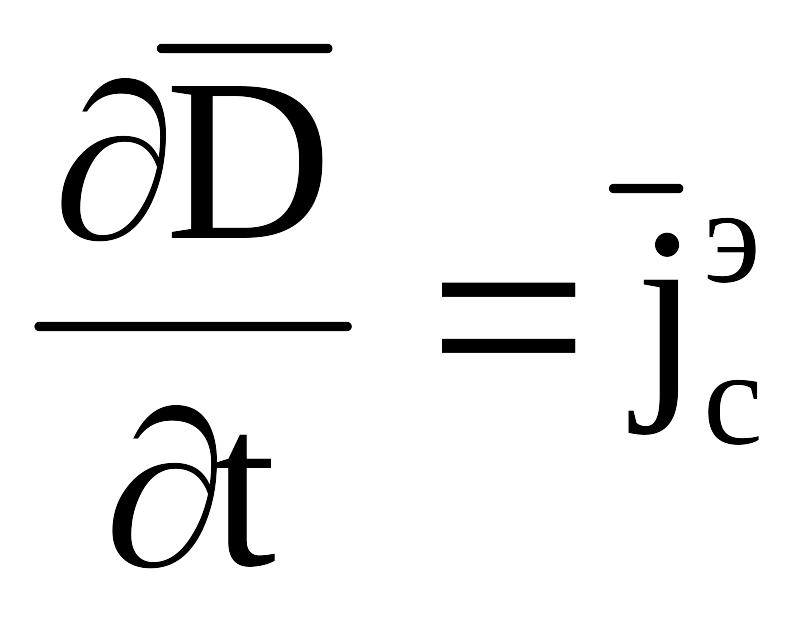
(7).

Аналізуючи (6), Максвелл сформулював одне з двох своїх найважливіших положень:

Перше положення Максвелла: Змінне в часі електричне поле приводить до появи в просторі магнітного поля.

Запишемо (6) у вигляді проекцій:

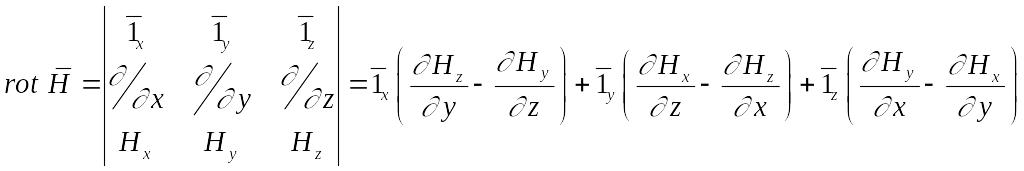
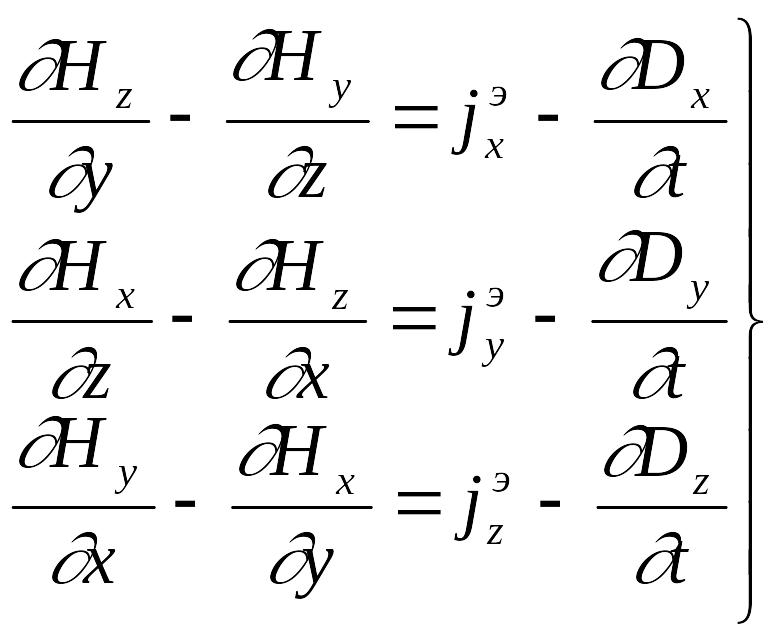(6')

Диференційній формі (6) відповідає інтегральна форма:

(8).