23Коши-Боняковский теңсіздігі.

Бағытталған кесінділер кеңістігінлегі сияқты кез келген ‹Х,Р› сызықтық кеңістігінің екі ɑ,b векторын, егер бір α,β ∈Р үшін b=αɑ немесе ɑ=βb болса, онда олар коллинеар векторлар деп аталаады.

‹Х,(,)› евклид кеңістігінің кез келген ɑ,b векторы үшін

(ɑ,b)²≤(ɑ,ɑ)(b,b) (і)

Коши-Буняковский теңсіздігі орындалады. Мұнда теңдік ɑ мен b коллинеар болғанда және тек сол жағдайда ғана орындалады.

Дәлелдеу.Егер ɑ,b вектордарының біреуі нөлдік вектор болса, онда теореманың тұжырцымы айқын. Сондықтан ɑ≠θ,b≠θ деп алып, ɑ-λb векторын қарастырайық.Мұндағы λ-кез келген нақты сан.Сонда

(ɑ-λb, ɑ-λb)=(ɑ,ɑ)-2λ(ɑ,b)+λ²(b,b) (іі)

Е3 және болуы үшін ɑ=θ болуы қажетті және жеткілікті- оң анықталғандық аксиома бойынша (ɑ-λb, ɑ-λb)≥0.Ендеше (1) теңдіктің оң жағындағы тұрған λ бойынша квадрат үшмүше теріс емес. Олай болса, оның дискриминанты оң емес , яғни 4(ɑ,b)²-4(ɑ,ɑ) (b,b)≤0.Осыдан (1) теңсіздікті аламыз.

Егер (1) теңдік орындалса квадрат үшмүшенің дискриминанты нөлге тең .Егер λ₀ үшмүшенің түбірі болса,онда(ɑ- λ₀b, ɑ- λ₀b)=0.Бұдан Е3 аксиомасы бойынша, ɑ= λ₀ b теңдігін аламыз.

ɑ мен bвектордары коллениар болсын . Сонда бір λ∈R үшін ɑ=λb.Осыдан

(ɑ,b)²=(λb,b)²=λ²(b,b)²= λ²(b,b) (b,b)= = (λb,λb) (b,b)= (ɑ,ɑ) (b,b)

Салдар (і.1) Евклид кеңістігінің кез келген ɑ,b векторлары үшін

(ɑ,b)≤|ɑ|·|b| (ііі)

Теңсіздігі орындалады, Осы теңсіздіктегі теңдік ɑ мен b коллинеар болған жағдайда және тек сол жағдайда ғана теңдік орындалады

Дәлелдеу:(ɑ,b)≤|(ɑ,b)| сандық теңсіздігін ескерсек,онда (ііі)-ші теңсіздіктің (і) –ші теңсіздікке эквивалент болатындығы айқын. Осы себептен (ɑ,b)≤|ɑ|·|b|

теңсіздікті де Коши-Буняковский теңсіздігі болады.

Кез келген α_і,β_і, і=1,n, нақты сандар үшін

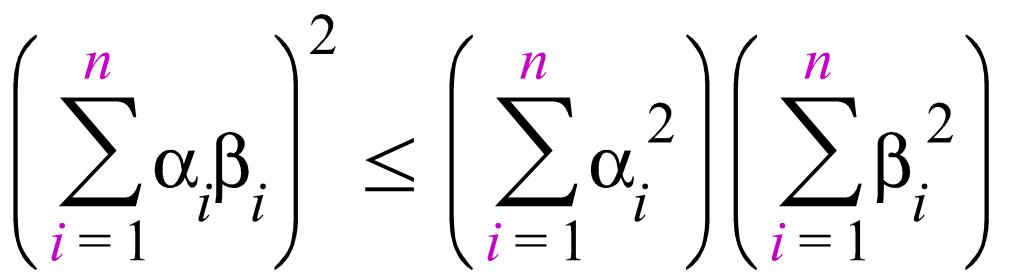(іііі)

Теңсіздігі орындалады. Сонымен қатар, (α₁, α₂, ...α_n)мен(β₁, β₂, ...β_n) жолдары пропорцинал болған жағдайда және тек сол жағдайда ғана (іііі)-ші теңсіздікте орындалады.

Дәлелдеу. Rⁿ –дегі нақты сызықтық кеңістігін қарастырайық та, скаляр көбейтіндіні

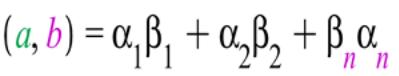
формула бойынша анықтайық . Сонда (іііі) теңсіздік осы скаляр көбейтінді бойынша Rⁿ –дегі Коши-Буняковский теңсіздігі болады.

25Ортогонал векторлар жүйесінің сызықты тәуелсіздігі туралы теорема

Х-Евклид не унитар кеңістік ,ал кез келген векторлар болсын.Егер(ɑ,b)=0 болса, онда ɑ,b ортогональ векторлар деп аталады.Егер вектор жүйесінің кез келген екі векторы өзара ортогональ болса, онда ол ортогонль жүйе деп аталады.

Нөлдік вектор кез келген векторға ортогональ .Шынында да,(θ,ɑ)=(0·ɑ,ɑ)=0·(ɑ,ɑ)=0.Кері тұжырымда орындалады: егер векторы кез келген векторына ортогональ болса ,онда b=θ.Шынында да,кез келеген үшін (b,ɑ)=0болса, онда дербес ɑ=b жағдайда да(ɑ,ɑ)=0болады.Олай болса Е3және болуы үшін θ болуы қажетті және жеткілікті- оң анықталғандық аксиомасы мен

U3 және аксиомасы бойынша b=θ.

Теорема.Нөлдік емес векторлардан тұратын ортогональ жүйе сызықтық тәуелсіз болады.

Дәлелдеу ɑ₁ ,ɑ_2,... ,ɑ_к нөлдік емес векторлар жүйесі ортогональ болсын.Қандай да бір ɑ₁ ,ɑ_2,... ,ɑ_к сандары үшін α₁ɑ₁+ α₂ɑ₂+...+ α_кɑ_к=θ теңдігі орындалсын. Осы теңдікті ɑ₁ векторына оң жағынан скаляр көбейтіп,

α₁(ɑ₁, ɑ₁)+ α₂(ɑ₂, ɑ₁)+...+ α_к(ɑ_к, ɑ₁)=(θ ,ɑ₁)=0

аламыз. (ɑ₂,ɑ₁)= (ɑ₃,ɑ₁)=...= (ɑ_к,ɑ₁)=0, ал (ɑ₂,ɑ₁)≠0 болғандықтан, ɑ₁=0. Енді α₂ɑ₂+ α₃ɑ₃+...+ α_кɑ_к=θ теңдігін ɑ₂ векторына оң жағынан көбейтіп, ɑ₂=0 теңдігін аламыз.Осы жолмен барлық ɑ_і,і=1,к, коэфициенттерінің міндетті түрденөлге тең болатындығы шығады.Ендеше ɑ₁ ,ɑ_2,... ,ɑ_к векторлар жүйесі сызықты тәуелсіз.