21.Біртекті сатж-ның шешімдер кеңістігі.

Алгебралық біртекті сызықтық теңдеулер

A•x=ө (1)

жүйесінің шешімдер жиынын L_Aдеп белгілейік. Pⁿсызықтық кеңістігінің L_Aішкі жиынын Х сызықтық кеңістігінің φ^-1(L_A) ішкі жиынының сипаттауы деп қарастырамыз.

(1)-ші алгебралық біртекті сызықтық теңдеулер жүйесінің L_A шешімдер жиыны Pⁿсызықтық кеңістігінің ішкі кеңістігі болады. Сол теңдеулер жүйесінің фундаментал шешімдер жүйесі L_Aішкі кеңістігінің базисі болады.

Дәлелдеу. (1)-ші теңдеулер жүйесінің x=(0,0,…,0)` нөлдік шешімі бар. Демек, L_A≠Ø. Кез келген a,b L_Aшешімдерін және кез келген α,β коэффиценттерін алып,αa+βb векторының (1)-ші теңдеулер жүйесінің шешімі болатынын көрсетейік.

A•(αa+βb)=α(A•a)+β(A•b)=α +β• =

Онда,αа+βb L_A. L_Aжиыны Pⁿсызықтық кеңістігінің ішкі кеңістігі болады.

a₁,a₂,…,a_k Pⁿбағандар жүйесі (1)-дің фундаментал шешімдер жүйесі болсын. Онда фундаментал шешімдер жүйесінің анықтамасы бойынша, бұл бағандар L_Aішкі кеңістігіне тиісті, a₁,a₂,…,a_k векторлар жүйесі сызықтық тәуелсіз және кез келген a L_Aшешімі a₁,a₂,…,a_k шешімдері арқылы сызықтық өрнектеледі. Демек, a₁,a₂,…,a_k векторлар жүйесі L_Aсызықтық кеңістігінің базисі болады.

22 Евклид кеңістігі

Егер Х нақты саны сызықты кеңістік ал (,) сол сызықтық кеңістіктегі скаляр көбейтіндісі болса, ˂Х,(,)˃ жұбы Евклид кеңістігі деп аталады.

Х кез келген нақты сызықтық кеңістік, ал f:Х*Х->R қандай да бір бейнелеу болсын. Бейнелеуін Х сызықтық кеңістігінің әрбір (a, b) веторлар жұбына f нақты саны сәйкес қоятын ереже деп түсінуге болады.Егер бұл ереже үшін үш аксиома:

Е1 -комутативтік аксиома;

Е2 -бірінші айнымалы бойынша сызықты аксиома.

Е3 және болуы үшін θ болуы қажетті және жеткілікті- оң анықталғандық аксиома;

Орындалса,онда ол скаляр көбейтінді деп аталады.

Скаляр көбейтіндінің алгебралық қасиеттері.

Е3 аксиомасының мынадай геометриялық мағынасы бар:вектордың ұзындығының квадраты теріс емес сан болады жіне ол сан нөлге тең болуы үшін вектордың өзі нөлдік болуы қажетті және жеткілікті.

Е2 аксиомасының келесі екі аксиомаға пара-пар болатыдығы айқын:

Е2а -скаляр көбейтінді бірінші айнымалы бойынша аддитив;

Е2б -скаляр көбейтінді бірінші айнымалы бойынша біртекті .

Е1-Е3 аксиомалпрынан скаляр көбейтіндінің төмендегі қасиеттері шығады

• (θ,α)=(α,θ)=0-кез келген векторды нөлдік векторға скаляр көбейткенде нөлдік сан шығады;

• (ɑ,βb+γс)=β(ɑ,b)+γ(ɑ,с)-скаляр көбейтінді екінші айнымалы бойынша да сызықтық болады;

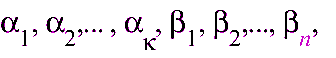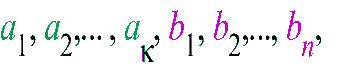• Кез келген нақты сандар мен кез келген векторлары үшін

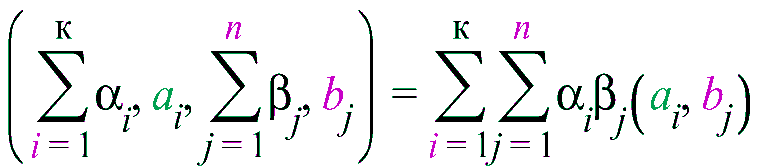
яғни, екі сызықты өрнекті көбейту үшін оларды мүшелеп көбейтуге болады.

• Егер кез келген b векторы үшін (ɑ,b)=0 болса 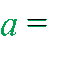θ

Сонымен, Евклид кеңістігі дегеніміз,өзінде қосымша анықталған қандай да бір скаляр көбейтіндімен бірге қарастырылатын нақты сызықтық кеңістік болады.Бір нақты сызықтық кеңістікте неше түрлі скаляр көбейтінді енгізуге болады.Ендеше,бір нақты кеңістікте әртүрлі Евклид кеңістіктерінің тұғыры болуы мүмкін.

Мысал:Егер (Мысал: _{және қандай да бір ɑ,b бағытталған кесінділерінің Декарт Базисіндегі координаталары болса,онда}

_(ɑ,b)=

_{Егер арифметикалық кеңістігінің кез келген векторлары болса,онда}

формуласы R кеңістігінде скаляр көбейтіндіні анықтайды. Өйткені, R кеңістігінің

Стандарт базисінде кез келген вектордың координаталық бағанын табу үшін сол векторды жай ғана аудару керек.