9. Векторлар жүйесінің сызықты комбинациясы мен сызықты қабықшасы.

Анықтама1: <X,P> сызықтық кеңістігінде кез келген a_1,a₂,...,a_k векторларының жүйесі берілсін.Осы векторлардан құрылған барлық сызықтық өрнектерден тұратын жиынын a_1,a₂,...,a_k векторларының сызықтық қабықшасы,ал a_1,a₂,...,a_k векторларын L(a_1,a₂,...,a_k) сызықтық қабықшасының жасаушылары деп атаймыз.

Әрине,L(θ)={θ} яғни нөлдік вектордың сызықтық қабықшасы нөлдік кеңістік болады. L(a_1,a₂,...,a_k) €X қатынасы да анық.Осыдан

кері қатынасының оындалуы X= L(a_1,a₂,...,a_k) теңдігіне пара-пар болатындығы шығады. Келесі мысалдарға негізгі сызықтық кеңістіктер сызықтық қабықшалар ретінде сипатталады.

Мысал1: L түзу бойында кез келген a≠θ векторын,П жазықтығында коллинеар емес a,b векторларының кез келген жұбын,сондай-ақ S сызықтық кеңістігінде компланар емес a,b,c векторларының кез келген үштігін алсақ,ондаL=L(a),П=L(a,b),S=L(a,b,c).

Жазықтықтан кез келген 0 нүктесін алып,осы 0 нүктесі басы болатындай етіп -2ậ векторын саламыз.Енді -2ậ векторының ұшымен (1/3)ḃ векторының басы беттесетіндей етіп (1/3)ḃ векторын векторының басы беттесетіндей етіп 4ḉ векторын саламыз.0 нүктесі мен 4ḉ векторының ұшын қоссақ сынықты тұйықтайтын вектор бізге қажетті ізделінді сызықтық комбинация.

Мысал2:Векторлар ортанормаланған i,j,k базисінде координаталарымен берілген.a=(2,-1,8), e₁=(1,2,3), e₂=(1,-1,-2), e₃=(1,-6,0). e₁,e₂,e₃ векторлары базис құрайтындығын дәлелде және осы базисте a векторының коордтнатасын тап. e₁,e₂,e₃ векторларының координаталарынан құралған анықтауыш

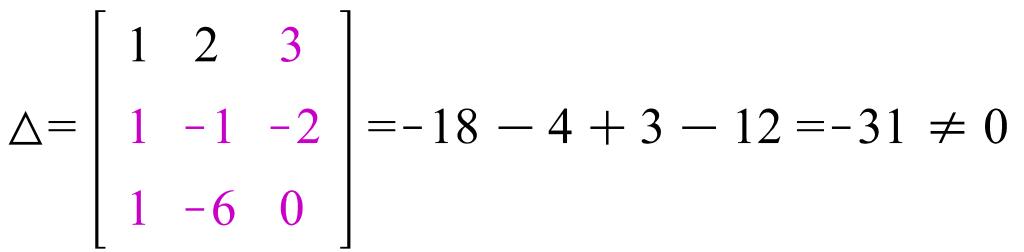
Ендеше e₁,e₂,e₃ векторлары сызықтық тәуелсіз,яғни,базис құрайды.а векторының e₁,e₂,e₃ базиндегі координаталарын x,y,z арқылы белгілейік Онда a=(x,y,z)=xe₁+ze₃.Есептің шарты бойынша a=2i-j+8k,e₁ теңдігінен +(2x-y-6z)j+(3x-2y)k шығады.Бұдан:

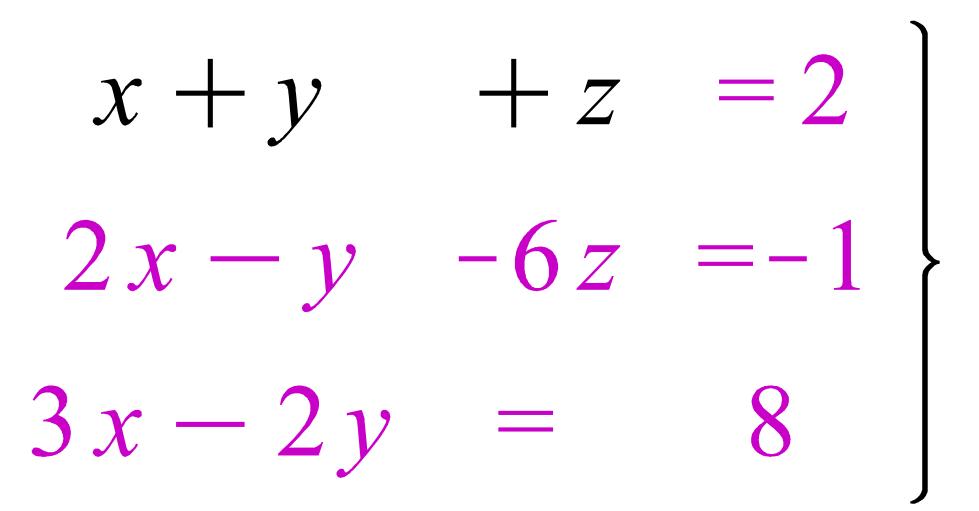
10.Векторлар жүйесінің сызықты тәуелділігі мен тәуелсіздігі.Қасиеттері.Белгілері.

а₁,а₂,...,а_n векторлар жүйесінің сызықтық өрнегі деп, α₁a₁+ α₂a₂+...+ α_na_n түріндегі өрнекті айтамыз.Мұндағы α₁,α₂,...,α_n нақты сандары осы сызықтық өрнектің коэффициенттері деп аталады.

Егер кейбір α₁α₂,...,α_n нақты сандар үшін b=α₁a₁+ α₂a₂+...+ α_na_n болса,онда b векторы a₁, a₂,...,α_n векторлары арқылы сызықтық өрнектеледі дейміз.

1.1-анықтама:Егер α₁a₁+ α₂a₂+...+ α_na_n=Ө теңдігі тек α₁=+ α₂=...=α_n=0 болған жалғыз жағдайда ақиқат болса,онда а₁а₂,...,а_n векторлар жүйесі сызықтық тәуелсіз деп аталады.

1.2-анықтама:Егер Ө-ны а₁а₂,...,а_n векторлары арқылы ең болмағанда коэффиценттерінің біреуі нөлден өзгеше болатындай сызықтық өрнектей алсақ: Ө=α₁a₁+ α₂a₂+...+ α_na_n, онда а₁а₂,...,а_n векторлар жүйесі сызықты тәуелді деп аталады.

Демек,берілген а₁а₂,...,а_n векторлар жүйесінің сызықтық тәуелділігі не тәуелсіздігін анықтау үшін белгісіздері а₁а₂,...,а_n болатын α₁a₁+ α₂a₂+...+ α_na_n=Ө теңдеуінің нөлдік емес шешімдері бар-жоқтығын зерттеуіміз керек.

Сызықтық тәуелділіктің қасиеттері.

1.1-қасиет.Егер а₁а₂,...,а_n векторлар жүйесінде нөлдік вектор кез болса,онда бұл жүйе сызықтық тәуелді болады.

Дәлелдеу.Анықтық үшін а_n=Ө болсын.Онда 0*a₁+ 0*a₂+...+ 0*a_n-1+1*a_n =Ө,демек а₁а₂,...,а_n сызықтық тәуелді жүйе.

1.2-қасиет.Жалғыз вектордан тұратын жүйе сызықтық тәуелді болуы үшін бұл вектордың нөлдік вектор болуы қажетті және жеткілікті.

Дәлелдеу.Егер жалғыз a₁ векторы нөлдік вектор болса,онда бұл жүйе 1.1-қасиет бойынша,сызықтық тәуелді.Кері жағдайда,яғни a₁≠Ө болғанда, α*a₁=Ө теңдеуінің α=0 шешімінен өзге шешім жоқ болатыны айқын.Ендеше нөлден өгеше жалғыз вектор сызықтық тәуелсіз жүйені құрайды.

1.3-қасиет.Егер сызықтық тәуелді жүйеге бірнеше вектор қоссақ,онда жаңа жүйе де сызықтық тәуелді болады.

1.4-қасиет.Сызықтық тәуелсіз жүйеден бірнеше векторларды алсақ,қалған векторлар да сызықтық тәуелсліз жүйені құрайды.

1.4-қасиет 1.3-қасиеттің салдары болатыны айқын.

1.5-қасиет. а₁а₂,...,а_n(n≥2) векторлар жүйесінің,сызықтық тәуелді болуы үшін осы векторлардың кем дегенде біреуінің қалған векторлар арқылы сызықтық өрнектелуі қажетті және жеткілікті.

Дәлелдеу.Қажеттілік. а₁а₂,...,а_n жүйесі сызықтық тәуелді болсын,яғни α₁,α₂,...,α_n нақты сандары табылып α₁a₁+ α₂a₂+...+ α_na_n=Ө,ал α₁,α₂,...,α_n сандарының арасында ең болмағанда біреуі нөлден өзгеше.Анықтық үшін α_n≠0 болсын.Онда

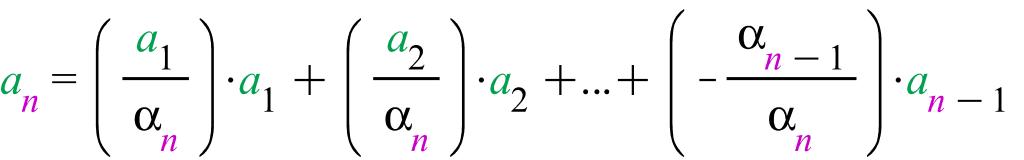
Жеткіліктілік.Анықтық үшін a_n=β₁a₁+...+β_n-1a_n-1 болсын,онда β₁a₁+...+β_n-1a_n-1+(-1)*a_n=Ө. Соңғы өрнектегі a_n вектордың коэффициенті нөлден озгеше,α₁,α₂,...,α_n жүйесі сызықтық тәуелді.