44.Айналу денелері және олардың көлемдерін есептеу (жоқ)

Егер кеңістікте бір сызық берілген осьті айналса, оның айналуынан бет п.б. Айналушы сызықтың формасына байланысты бет әр түрлі болады. Мысалы, егер шеңбер өзінің диаметрі бойынша айналса, сфералық бет шығады, ал координаталар басынан өтетін түзу OZ осін айналса, дөңгелек конус п.б. Сызықтың айналатын осін айналу осі, ал пайда болған бетті айналу беті деп атайды. Бізге YOZ жазықтығында жатқан L сызығы f ( y, z ) = 0 теңдеуімен берілсін. Осы сызықтың OY осін айналғанда пайда болған беттің теңдеуін табу үшін сол сызықтың f ( y, z ) = 0 ± x 2 + y 2 өрнегімен алмастыру теңдеудегі y – ті өзгертпей, z – ті керек. Сонда айналу бетінің теңдеуі мынандай болады: Басқа осьтерді айналғанда пайда болған беттердің де теңдеулері осыған ұқсас табылады. Яғни, егер берілген сызық OZ осінен f (x ± x 2 + y 2 ) = 0 айналса, онда айналу бетінің теңдеуі болады.

Айналу денелерінің көлемдері

Цилиндрдың көлемі

Егер берілген денені қамтитын және осы дене ішінде

қамтылатын,кӛлемдерінің V-ден айырмашылығы барынша аз,қарапайым

денелер бар болса, онда берілген дененің кӛлемі v болады.

Цилиндрдің көлемі табанының ауданы мен биіктігінің көбейтіндісіне тең

болады.

V=SH=πR2H

Конустың көлемі

Конустың кӛлемі табанының ауданы мен биіктігінің көбейтіндісінің үштен

біріне тең болады.

V=(1/2)SH=(1/3)πR2H

45. Эллипсоид және оның түрлері. Канондық теңдеуін қорыту.

(1)

Егер a=b=c=R болса, онда (1) эллипсоид центрі координата басында , радиусы R ға тең сфераға айналады:

(1’)

а,b,c – эллипсоидтың жарты өстері деп аталады.

(1) теңдіктен эллипсоидтың х=0, у=0,z=0 координаталық жазықтықтарға салыстырғанда және координата басына салыстырғанда симметриялы болатынын көреміз.

Эллипсоидтың z=h‚-c≤h≤c жазықтықтарымен қимасы –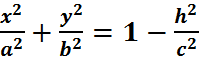

_Немесе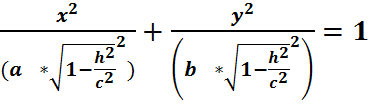

түріндегі эллипстер.

Жарты өстері z=0, (h=0) болса, ең үлкен мәнге ие болғандықтан, бұл мәнге (z=0, (h=0)) сәйкес эллипс те үлкен болады.Осы сияқты жағдайлар эллипсоидтың x=h, және жазықтықтарымен қимасында да болады.

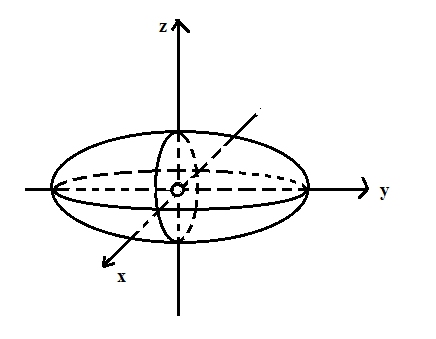
Эллипсоидтың (±а,0,0) , (0,±b,0), (0,0,±c) нүктелері, оның төбелері деп аталады.

Егер эллипсоидтың қандай да бір жарты өстері өзара тең болса, онда эллипсоид эллипстің сәйккес координата өсі арқылы айналуынан шығады да, оны айналу эллипсоиды деп атайды.

Дербес жағдайда z=0 жазықтықпен қимада

шығады. Эллипсоидттың х=h, у=h жазықтықтарымен қималары да осылайша анықталады. Эллипсоидтың координата жазықтықтарына параллель жазықтықтарымен қимасында эллипстер пайда болады..

Егер тікбұрышты декарт координаталар жүйесінде екінші ретті бет

Теңдеуімен берілсе, онда ол екінші ретті жорамал эллипсоид деп аталады. Кеңістіктің бірде-бір нүктесінің координаталары теңдеуін қанағаттандырылмайтыны түсінікті.Егер тікбұрышты декарт координаталар жүйесінде екінші ретті бет

Теңдеуімен берілсе, онда ол жорамал конус деп аталады. Бұл теңдеуді жалғыз О(0,0,0) нүктесі қанағаттандырады. Кейде бұл теңдеумен берілген бетті өзгеше эллипсоид деп те атайды.