41. Инерция заңы. Теорема

Квадраттық форманы канондық түрге келтіргенде кейбір квадраттардың алдындағы таңба оң, кейбіреулерінікі теріс болуы мүмкін.

Басқа базистерде квадрат форма бөлек жазылуы мүмкін.

Осындағы оң квадраттардың санын квадрат форманың оң индексі деп атайды. P=p(f), n=m(f)

Ал барлық квадраттардың санын (p+n) квадрат форманың рангысы деп атаймыз.

Нақты квадраттық форма осы форманы қалыпты түрге келтіру тәсіліне тәуелді емес.

Теорема.(инерция заңы)

Квадрат форманы қандай жолмен канондық түрге келтірсек те, ондағы оң квадраттардың саны мен сол квадраттардың саны тең. k=l, s=q.

Дәлелдеуі: Квадрат фома базисінде (2) түрге,

базисінде (1) түрге келтірілсін. Мұнда k< l

n + (l -k)>n

k+s = l+q =r деп алайық.

R₁ арқылы базистік векторлары арқылы құрылған кеңістікті белгілейік.

Және

_және

K< L=> K L

L K=>K=L=>S=q

Салдар:

1. Квадраттық форманы канондық түріндегі оң коэффиценттері саны осы квадраттық форманы канондық түрге келтіру тәсіліне тәуелді емес. Квадраттық форманы канондық түріндегі оң коэффиценттері мен тері коэффиценттерінің айырмасы k-l=s осы форманың сингатурасы деп аталады.

2. Квадраттық форманың сингатурасы сол форманың канондық түрге келтірудің тәсіліне тәуелді емес.

42. Оң және теріс анықталған. Сильвестор белгісі

Таңбасы анықталған квадраттық формалар

Егер ∀а€Е(а≠0) үшін f(а)>0⇒ бұл квадраттық форманы оң анықталған квадраттық форма деп атаймыз.

Егер ∀а€Е(а≠0) үшін f(а)<0⇒ бұл квадраттық форманы сол анықталған квадраттық форма деп атаймыз.

∀а€Е үшін f(а)≥0[f(а) ≤0] жартылай оң анықталған (жартылай теріс анықталған) квадраттық форма деп аталады.

_,

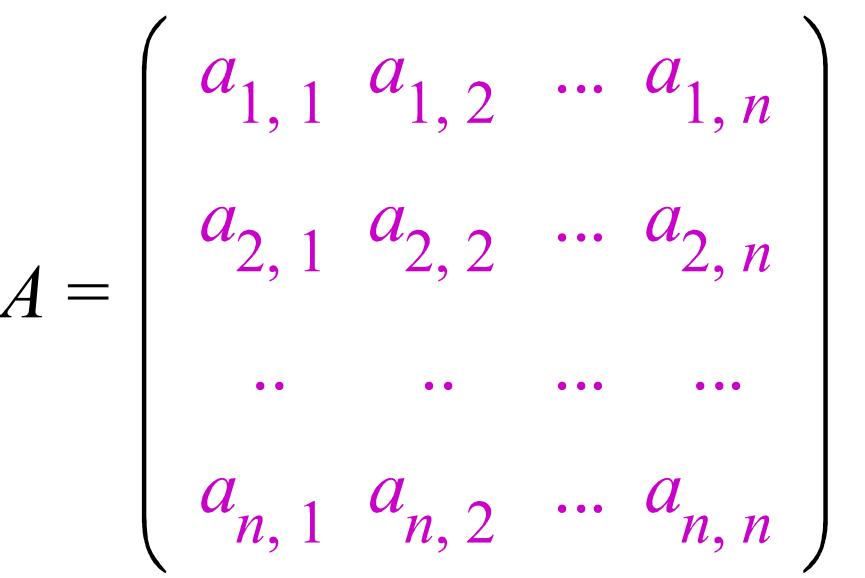
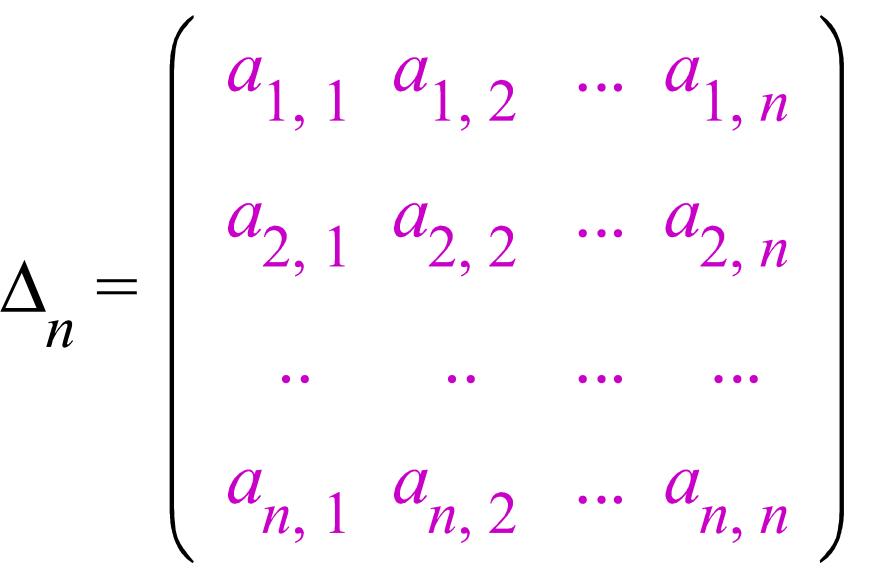
Анықтауыштары А матрицасының бұрыштық минорлары

Лемма 1

f(х) функциясы оң (теріс) анықталған болады, сонда тек сонда ғана

_{квадрат форманың бұл базистегі матрицасы}

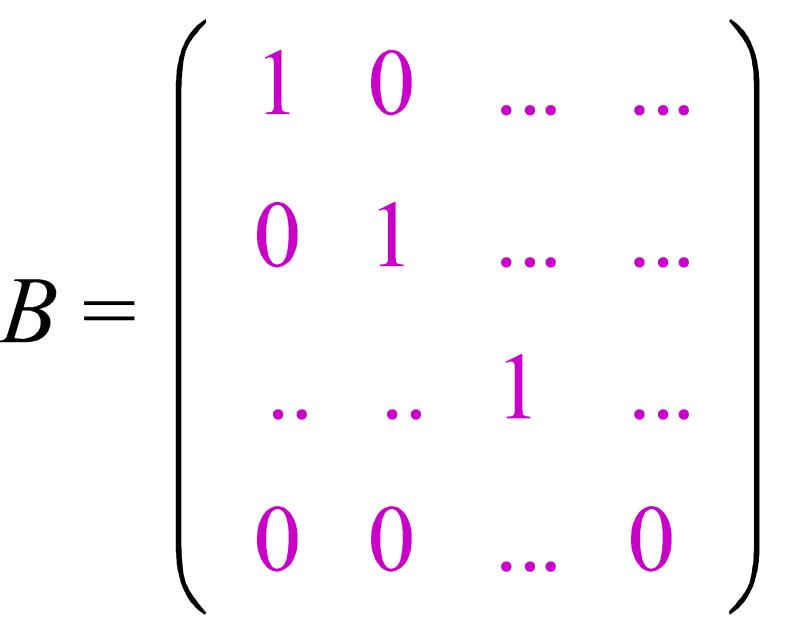
Әр түрлі базистегі матрицалар арасында байланыс бар және

Теорема (Сильвестор белгісі).

Квадрат форманың оң анықталуы үшін оның матрицасының барлық бұрыштық минорларының оң болуы қажетті және жеткілікті.

Функция оң анықталады :

(1)

_{Қажеттілік:}

Дәлелдеуі:

Айнымалылар саны бойынша индукция әдісі арқылы жүргіземіз.

Айнымалылар саны п-1 ге тең болатын барлық оң анықталған квадрат формула үшін (1) шарт орындалады.

Осы квадрат функциядағы f1 квадрат формадағы оң анықталған болуы керек. Егер қандай да бір үшін үшін

f формасы оң анықталғандықтан қайшы және оның бұрыштық минорлары А матрицасының алғашқы (n-с) бұрыштық минорларымен бірдей

Лемма бойынша f квадрат формасы мынадай түрге келеді:

Квадрат формасы теріс анықталуы үшін оның бұрыштық минорларының таңбалары теріс таңбадан бастап кезектесіп отыруы қажетті және жеткілікті.

43.Екінші ретті беттер. Коникалар.

L түзуі берілсін. Өзінің әрбір нүктесімен бірге, осы нүктеде L түзуін айналғанда пайда болатын шеңберді қамтитын кеңістіктегі бетті айналу денесі д.а.

a₁₁x²+ a₂₂y²+a₃₃z²+2a₁₂xy+2a₁₃xz+a₂₃yz+a₁x+a₂y+a₃z+a₀=0 (1)

теңдеуді қанағаттандыратын кеңістіктегі геометриялық нүктелер орнын екінші ретті алгебралық бет д.а.

Екінші ретті беттер 10 типке бөлінеді. Олар:

Эллипсоид

Жорамал эллипсоид

Өзгеше эллипсоид

Бір қуысты гиперболоид

Екі қуысты гипенболоид

Эллипстік параболоид

Конус

Гиперболалық параболоид

Цилиндр(эллипстік цил-р, жорамал элл-к цил-р, гиперб-қ цил-р, парабол-қ цил-р, қиылысатын жазықтықтар жұбы, қиылысатын жорамал жазықтар жұбы)

10, Жазықтардың параллель жұбы, жорамал параллель жұбы, беттескен жұп

1. + =1 , a≥b≥c>0, эллипсоид

2. + =-1 , a≥b≥c>0, жорамал элл-д

3. + =0 , a≥b≥c>0, өзгеше элл-д н-е конус

4. + =1 , a≥b>c>0, бір қуысты гиперболоид

5. - =-1 , a≥b>0, c>0, екі қуысты гип-д

6. - =0 , a≥b>0, c>0, конус

7. =z , a≥b>0, элл-к параб-д

8. , a>0, b>0, гип-қ параб-д

14. y²=2px, p>0, параб-қ цил-р

15. y²-b²=0, b>0, жазықтардың параллель жұбы

16.y²+b²=0, b>0, жорамал параллель жұп

17. y²=0 беттескен жұп