39. Жордан клеткалары.Жордан матрицасы. Жордан матрицасына келтіру мысалдары.

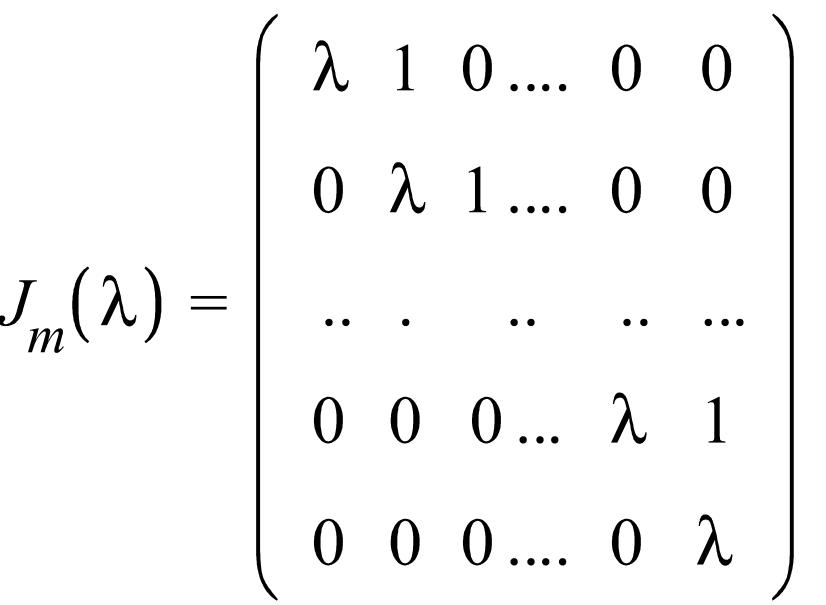
Бұл матрицадағы λ өзіндік мәніне сәйкес Жордан ұяшығы, ал диагонал блоктары Жордан клеткалары болатын блокты-диагонал матрицаны Жордан түріндегі матрица деп атайды.

Теорема. А€L(Х,Х) сызықты операторының сипаттауыш көпмүшесінің канондық жіктеуі бар болсын. Онда Х кеңістігінің канондық базисіндегі оператордың матрицасы Жордан түріндегі матрица болады.

Дәлелдеу:

1. Опенратордың канондық базисі нильпотент тізімдерден, ал оның Жордан түріндегі блокты-диагонал матрицасы Жордан клеткаларынан түзіледі.

2. Әр нильпотент тізіміне тура бір Жордан клеткасы сәйкес келеді.

3. Нильпотент тізіміне қатысты өзіндік мәні сәйкес Жордан клеткасының бас диагоналінде орналасады.

4. Нильпотент тізіммен туындалатын циклдік ішкі кеңістіктің өлшемділігі мен сәйкес жордан клеткасының реті бірдей болады.

Осыдан Жордан түріндегі матрицаның құрамы А операторының инварианты болатыны оңай шығады. Теорема дәлелденді.

Диагоналында жордан секторлары орналасқан n- ші ретті матрицаны біз жордан түріндегі матрица деп атаймыз.

Диагонал жордан клеткалары орналасқан.

(n=k) m₁+…+m_k=n

n – ші ретті матрицаны біз жордан түріндегі матрица деп атаймыз. λ=2

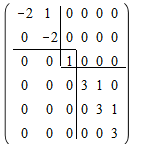6 –шы ретті жордан матрицалары

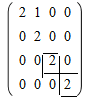
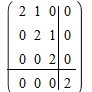
4=3+1=2+2=2+1+1=4+0

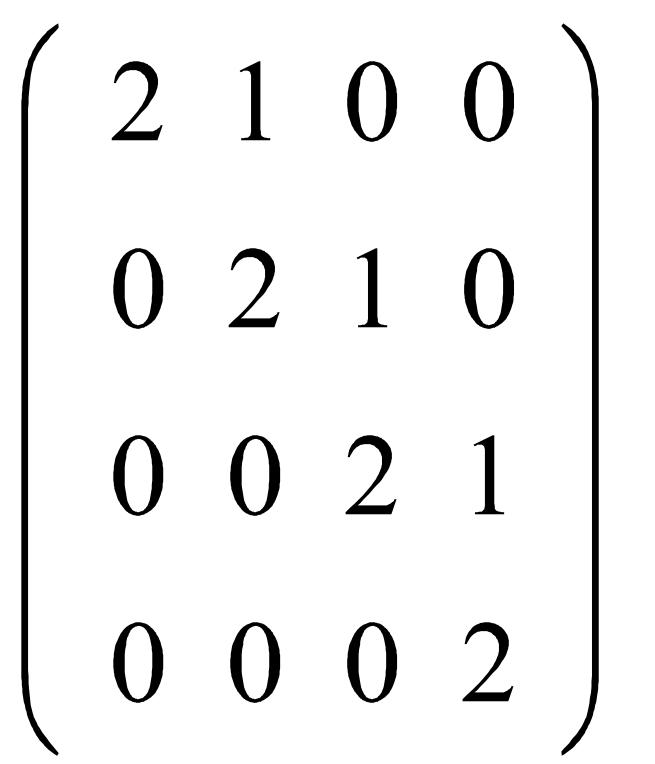
Жордан матрицасына мысал:

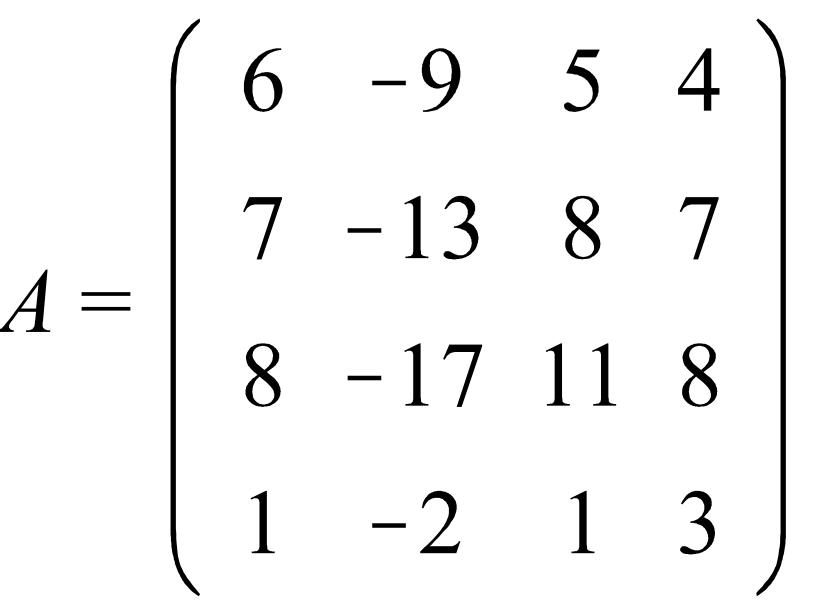
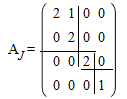жордан матрицасы

Негізгі формуласы

40.Шаршы тұлғалар. Шаршы тұлғаларды канондық түрге келтіру. Лагранж әдісі.

Айнымалылары х1,...,хn болатын, дәрежесі екіге тең нақты көпмүшесі шаршылық тұлға деп аталады. Яғни шаршылық тұлға дегеніміз: Түріндегі өрнек болады. Бұл жерде

_{көпмүшесінің барлық мүшелерінің дәрежелері бірдей болғандықтан, ол біртекті болады. aij Сандары F шаршылық тұлғасының матрицасы деп аталады. F көпмүшесінің дәрежесі екіге тең болуы үшін, aij коэффиценттерінің кем дегенде біреуі нөлден өзге боуы қажет.}

Анықтама: Матрицасы диагонал болатын шаршылық тұлғаның түрі канондық деп аталады. Басқа сөзбен айтқанда, түріндегі көпмүше канондық шаршылық тұлға, ал оның матрицасы болады.

Әрбір шаршылық тұлға кем дегенде бір канондық түріндегі шаршылық тұлғаға конгруэнт болады, яғни әрбір шаршылық тұлғаны канондық түрге келтіруге болады.

Лагранж әдісі.

Лагранж әдісі дәрежесі екіге тең біртекті көпмүшелерден толық шаршы өрнектерді бөліктеп алу әдісіне негізделген.

шаршылық тұлғасы _{Шаршылық тұлғасына ауыстырайық. Мұндағы шаршылық тұлғасының айнымалылары саны ең көп дегенде n-1 болатыны айқын. айнымалыларын айнымалыларына көшіретін у=Q*x сызықты түрлендіруінің матрицасы}

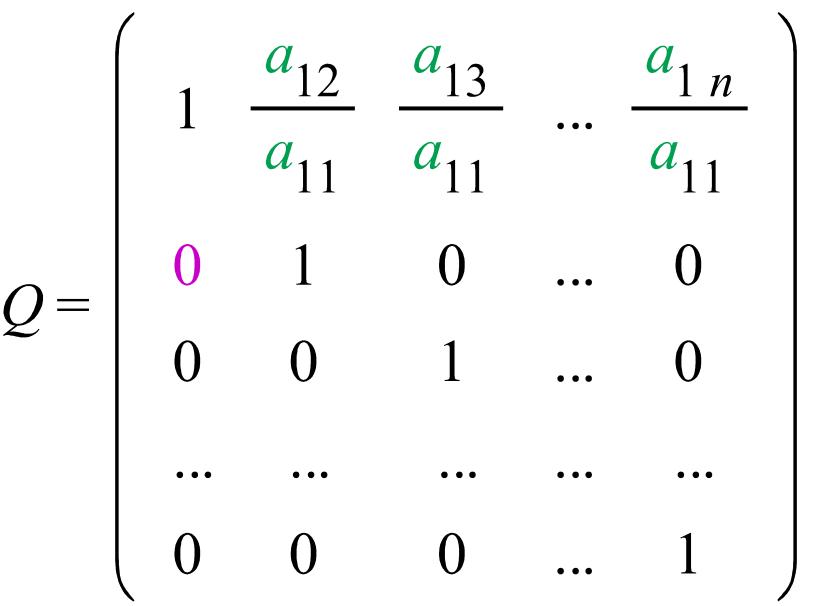
_{ерекше емес болатыны бірден көрініп тұр. Жоғарыдағы шаршылық тұлғасынан шаршылық тұлғасына көшіруді Лагранж тәсіліндегі шаршылық тұлғаларлың бірінші түрлендірілуі деп аталады.}

_{Лагранж түріндегі шаршылық тұлғалардың екінші түрлендірілуі. Барлық aij}

Диагонал коэффиценттері нөлге тең болғанда, кем дегенде бір айнымалының квадраттарының алдыңғы коэффицентін нөлден өзге болатындай, қосымша түрлендіру жасау керек. deg(F)=2болғандықтан, аралас мүшелерінің кем дегенде бір коэффиценті нөлден өзгеше.

Берілген шаршылық тұлғаны канондық түрге келтіру үшін бірінші түрлендіруді мейлінше мүмкін болғанша жасау керек.Ал ондай мүмкіндік таусылғанда, екінші түрлендіруді жасап алып, бірінші түрлендіруге қайтып оралу керек. Егер шаршылық тұлғаның айнымалылар саны n ге тең болғанда, онда бірінші түрлендіру ең көп болғанда n-1 рет жасалғаннан соң бастапқы шаршылық тұлға канондық түрге келеді.