29Ортонормаланған базисті табу.

Евклид не Унитар кеңістігіндегі ɑ€Х векторының ұзындығы бірге тең, яғни |ɑ|=1 болса, онда ɑ нормаланған вектор деп аталады. Егер вектор жүйесінің әр векторы нормаланған болса, онда ол нормаланған жүйе деп аталады.Егер векторлар жүйесі бірдей ортогональ және нормаланған болса, онда ол ортонормаланған жүйе деп аталады.

Ортонормаланған жүйелердің арасында ең мағыздылары ортонормаланған базистер болып табылады.Ортонормаланған базистердің артықшылық қасиеттері.

е₁,е₂,..., е_n,векторлар жүйесі арқылы өлшемді Х Евклид не унитар кеңістігінің ортонормаланған базисі,ал

ɑ_е=(α_1,α₂,...,α_n)’, b_e=( β_1,β₂,...,β_n)’

бағандары ɑ,b векторларын е базисіндегі координаталық бағандар болсын.

Сонда

І. Х-Евклид кеңістігі де унитар кеңістікте болған жағдайларда кез келген і=1,n үшін.

ɑ_і=(ɑ,е_і) (1)

ІІ.Х- Евклид кеңістігі болған жағдайда

(ɑ,b)= α₁ β₁₊α₂ β₂+...+α_n β_n=(ɑ,е_і),

|ɑ|=

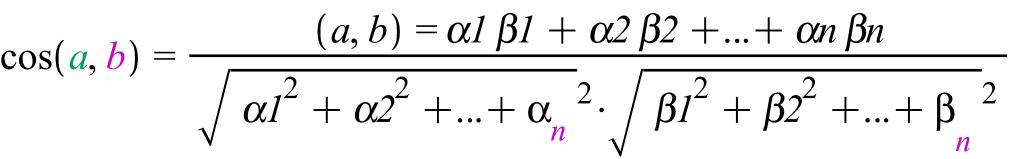
ІІІ. Х-Унитар болған жағдайда.

(ɑ,b)= α₁ β₁₊α₂ β₂+...+α_n β_n=(ɑ,е_і),

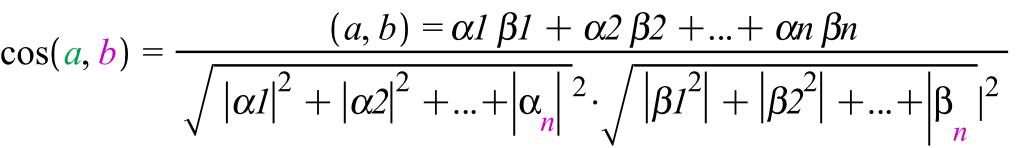
31Сызықты оператор.Оның өзегі мен бейнесі.

Х және У өандай да бір Р өрісі бойынша екі сызықтық кеңістік болсын.Егер кез келген.Егер кез келген α,β€ Р коэфициенттері мен кез келген+ векторлар үшін

А(αɑ+βb)= αАɑ+βАb (1)

орындалса, онда А:Х→У бейнелеу сызықты оператор деп аталады.Ал(1)-теңдіктегі А операторының қасиетін сызықтық қасиет деп атаймыз.

А:Х→У сызықтық операторы үшін Х сызықтыө кеңістігін бейнелейтін кеңістікғ ал х€ Х векторының Укеңістігіндегі Ах мәнін х векторының бейнесі деп атаймыз.

Сызықтық оператордың анықтамасындағы (1)-теңдік

А(ɑ+b)= Аɑ+Аb (2)

Және

А(αɑ) = αАɑ (3)

екі теңдікке пара-пар. (2)-теңдік А операторының аддитивтік қасиеті, ал бұндай қасиеті бар оператор аддитив оператор деп аталады.Сондай-ақ (3)-теңдік біртектілік қасиет деп, бұндай қасиеті бар оператор біртекті оператор деп аталады.Сонымен басқаша айтқанда,сызықтық оператор дегеніміз әрі аддитив,әрі біртекті оператор болып табылады.

Сызықты оператор қасиеттері

(1)-формуладан А(θ_Х) = θ_У (4)

Теңдігі және кез келген α₁, α₂,..., α_к€ Р ,ɑ₁, ɑ₂,..., ɑ_к€ Х үшін

А(α₁ɑ₁₊ α₂ɑ₂₊...+ α_кɑ_к)= α₁Аɑ₁₊ α₂Аɑ₂₊...+ α_kАɑ_k (5)

немесе, қысқаша түрде,

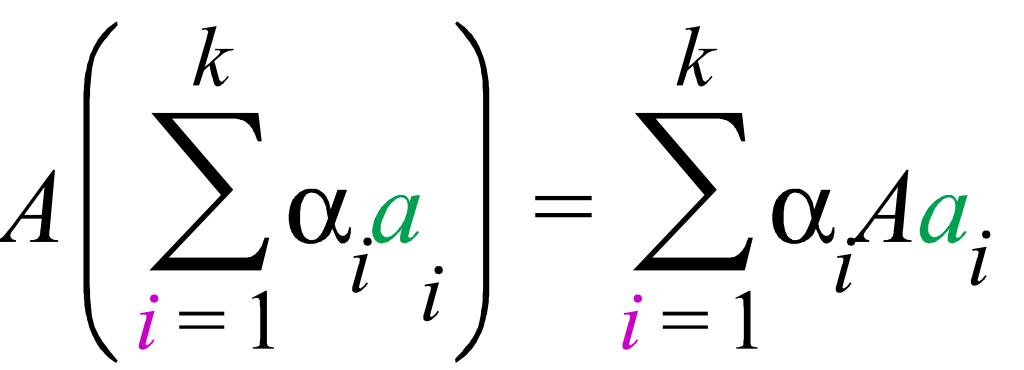(6)

Теңдігі орындалатындығы шығады.

(4)-теңдіктен сызықтық оператордың нөлдік вектордың бейнесі нөлдік вектор болатынын,ал(5)-теңдіктен сызықтық оператордың сызықтық өрнектерді сызықтық өрнектерді сақтайтыны көреміз. Осы екі теңліктен:сызықтық оператор сызықтық тәуелді векторлар жүйесін сызықты тәуелді векторлар жүйесіне көшіреді деген салдар шығады. Яғни , егер сызықтық кеңістігінің α₁, α₂,..., α_к векторлар жүйесі сызықтық тәуелді болса, онда олардың Аα₁, Аα₂,..., Аα_к бейнелері У кеңістігінің сызықтық тәуелді векторлар жүйесін құрайды. Ал, сызықтық тәуелсіздікті сызықтық оператор сақтамауы мүмкін.

А:Х→У операторынң өзгеру жиыны оның бейнесі, ал Ах=θ теңдеуінің шешімдер жиыны оның өзегі деп аталады.А операторының бейнесі мен өзегі сәйкес imA және kerA арқылы белгіленеді. Сонымен,

imA={y€ Y|Ǝx€X(y=Ax)}, ker={x€X|Ax=θ}

Тұжырым. Кез келген А:Х→У сызықтық операторының kerA өзегі Х сызықтық кеңістігінің ішкікеңістігі болады.

Дәлелдеу.Егер х₁,х₂€ kerA болса онда Ах₁ =θ, Ах₂ =θ.Өрістің кез келген α,β коэфициенттері үшін А(αх₁+βх₂)= αАх₁+βАх₂= θ.Демек kerA өзегі Х сызықтық кеңістігінің сызықтық өрнектер бойынша тұйық жиынан құрайды,ендеше, ол Х кеңістігінің ішкікеңістігі болады.

Егер + y₁,y₂ € imA болса,онда кейбір x_1,x₂ € X үшін Ax₁=y₁, Ax₂=y₂, болады да αy₁+βy₂= αАх₁+βАх₂= А(αх₁+βх₂).Демек imA бейнесі У сызықтық кеңістігіндегі сызықтық өрнектер бойынша тұйық жиын болады.

Тұжырым бойынша, аналитикалық геометриядағы әрбір сызықтық оператордың бейнесі мен өзегі не жалғыз θ векторы, не полюстен өтетін түзу,не полюстен өтетін жазықтық,не кеңістіктің өзі болады.Осы себептен олар нөлдік ішкікеңістігінен өзге шенелген жиын немесе жарты жазықтық немесе жарты кеңістік бола алмайды. Мысалы,бағытталған кесіндіге оның ұзындығын сәйкес қоятын Ах=|х| ереже сызықтық функция бола алмайды.