Часть 2

Ответом на каждое задание этой части будет число. Единицы измерения писать не следует (В1-В8).

В1. Найдите сумму корней уравнения: (sin3x*cosx-sinx*cos3x) =0.

В2. Найдите значение выражения .

В3. Найдите число целых решений неравенства

В4. Вычислите .

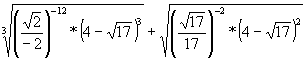В5. Найти наименьшее значение а, при котором неравенство ax²+(a-4)x-2>2,5 не выполняется ни при каких действительных значениях x.

В6. Решите уравнение: 1+2х+4х²+…+ +…=3,4-1,2х, если известно, что |x|<0,5.

В7. Решите систему уравнений

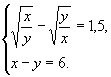
В8. Решите задачу:

Найти боковую поверхность правильной треугольной призмы с высотой h, если прямая, проходящая через центр верхнего основания и середину стороны нижнего основания, наклонена к плоскости основания под углом 60 .

Часть 3.

К заданиям этой части нужно записать полное решение (С1-С3).

С1. Определите, при каком значении а система уравнений 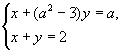имеет бесконечно много решений?

С2. Выразите через a и b , если a= и b= .

С3. Решите задачу:

Имеется некоторое количество раствора соли в воде. После добавления в раствор трех литров воды концентрация соли уменьшилась на 15%, а после испарения из получившегося раствора пяти литров воды концентрация соли стала в 3 раза больше первоначальной. Найдите концентрацию соли в исходном растворе, считая массу 1л воды равной 1кг.

Вариант 4.

Часть 1.

При выполнении заданий этой части укажите цифру, которая обозначает выбранный Вами ответ (А1-А15).

А1. Вычислите: .

1). 2). 0,56 3). 4). 1,12

А2. Упростите выражение: .

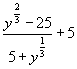1). y 2). y +10 3). y 4). y².

А3. Выражение равно:

1). -4 2). 256 3). 0 4). 4.

А4. Упростите выражение: .

1). -1-sin 2). 1+sin 3). 1 4).cos .

А5. Наименьший из корней уравнения 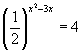равен:

1). 1 2). 2 3). 3 4). -2.

А6. Решите неравенство:

1). 2). 3). 4). .

А7. Найдите область определения функции:

1). 2). 3). 4). .

А8. Найдите множество значений функции: y=sin(x-5).

1). 2). 3). 4). .

А9. Укажите график зависимости, которая не является функцией:

1).

2).

3).

4).

А10. Найдите предел: .

1). 1 2). 3). 0 4). .

А11. Найдите количество корней уравнения 1-сtg =0 , удовлетворяющих условию -2<x<1

1). 1 2). 2 3). 3 4). 4.

А12. Сумма корней уравнения равна:

1). 2). 7 3). 4). 1.

А13. Количество корней уравнения tg из интервала равно:

1).5 2).1 3).3 4).2.

А14. Корни ( или корень, если он единственный) уравнения 3 принадлежит интервалу:

1). 2). 3). 4). .

А15. Решите задачу:

В спортивной секции девочки составляют 60% от числа мальчиков. Сколько процентов от числа всех участников секции составляют девочки?

1). 60 2). 37,5 3). 40 4). 50.