Вариант 1.
Часть 1.
При выполнении заданий этой части укажите цифру, которая обозначает выбранный Вами ответ (А1-А15).
А1.
Вычислите:
.
1). 9 2). 4,5 3). 3 4). 4
А2.
Упростите
выражение:
.
1).
-4 2). 4 3).
4).
.
А3.
Выражение
равно:
1).5 2). 25 3). 3 4). 2.
А4.
Упростите
выражение: cos2
-sin2
+1.
1). -2 sin2 2). 2 cos2 3). Cos2 4).2.
А5.
Наибольший
из корней уравнения
равен:
1). 2 2). 1 3). -1 4). -4.
А6.
Решите
неравенство:
1).
2).
3).
4).
.
А7.
Найдите
область определения функции:
1).
2).
3).
4).
.
А8.
Найдите
множество значений функции:
1).
2).
3).
4).
.
А9. Укажите график четной функции:
1). |
2). |
3). |
4). |
А10.
Найдите
предел:
.
1).
3
2).
1
3).
4).
2.
А11.
Найдите
количество корней уравнения
,
принадлежащих интервалу (0;
).
1). 5 2). 2 3). 3 4). 4.
А12.
Корень
уравнения
равен:
1). 5 2). -5 3). 0 4). -2.
А13.
Среднее
арифметическое корней уравнения
ctg2x+ctgx=0,
принадлежащих интервалу (0;
)
равно:
1).
2).
3).
4).
.
А14. Корень уравнения 32x+1-9x=18 принадлежит интервалу:
1). (-1;0,5) 2). (0;1,5) 3). (0;1) 4). (1;3).
А15. Решите задачу:
Яблоки содержали 80% воды. При сушке они потеряли 60% от своей массы. Сколько процентов воды содержат сушеные яблоки?
1). 32 2). 48 3). 50 4). 12.
Часть 2
Ответом на каждое задание этой части будет число. Единицы измерения писать не следует (В1-В8).
В1.
Сколько
корней имеет уравнение (cosx*cos3x+sinx*sin3x)
=0.
В2. Найдите значение выражения tg(2arctg3).
В3.
Найдите
число целых решений неравенства
(-5+cosx)(|3x-2|-1)
В4.
Вычислите
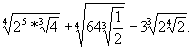
В5. При каком k парабола y=(k-1)x2 + (k+4)x + k+7 касается оси Ох.
В6. Сумма трех последовательных членов геометрической прогрессии равна 65, а сумма их логарифмов по основанию 15 равна 3. Найдите эти члены прогрессии.
В7.
Решите
систему уравнений
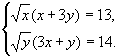
В8. Решите задачу:
Апофема
правильной шестиугольной пирамиды
равна h, а двугранный угол при основании
равен 60
.
Найдите полную поверхность пирамиды.
Часть 3.
К заданиям этой части нужно записать полное решение (С1-С3).
С1.
Определите,
при каких значениях k система уравнений
не
имеет решений.
С2.
Выразите
через a и b
если a
=
и b
=
.
С3. Решите задачу:
Если два сплава золота сплавить в отношении 3:7, то получится сплав, содержащий 87% золота. Если же эти сплавы сплавить в отношении 7:3, то получится сплав, содержащий 83% золота. Найдите процентное содержание золота в первом сплаве.
Вариант 2.
Часть 1.
При выполнении заданий этой части укажите цифру, которая обозначает выбранный Вами ответ (А1-А15).
А1.
Вычислите:
.
1).4,75 2). 8,75 3). 0,875 4). 6,25.
А2.
Упростите
выражение:
.
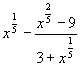1).
3
2).
-3
3).
4).
.
А3.
Выражение
равно:
1).81 2). 2 3). 3 4). 4.
А4. Упростите выражение: 1+ sin2 - cos2 .
1).
2 sin2
2). - cos2
3).1+сos2
4).2.
А5.
Наибольший
из корней уравнения
равен:
1). -1 2). -3 3). 1 4). 4.
А6.
Решите
неравенство:
1).
Ш
2).
3).
4).
.
А7.
Найдите
область определения функции:
1).
2).
3).
4).
.
А8. Найдите множество значений функции: y=2sin6x.
1).
2).
3).
4).
.
А9. Укажите график функции, которая не имеет нулей:
1). |
2). |
3). |
4). |
А10.
Найдите
предел:
.
1).
2).2
3).
4).
1.
А11.
Укажите
наименьший положительный корень
уравнения
1).
2).
3).
4).
0.
А12.
Корень
уравнения
равен:
1).
0
2).
3).
1
4).
нет корней.
А13. Множество корней уравнения 1+cos2x=sinx совпадает с множеством корней уравнения:
1). tgx=0 2). cosx=0 3). sinx=1 4).sinx=-1.
А14. Корень уравнения 4x+1-22x-2=60 принадлежит интервалу:
1). (-1;0,5) 2). (0;1,5) 3). (1;3) 4). (0;2).
А15. Решите задачу:
Цена доллара в рублях увеличилась на 25%. На сколько процентов при этом уменьшилась цена рубля в долларах?
1). 25 2). 75 3). 80 4). 20.