Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ивано-Франковский национальный технический университет нефти и газа

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

MTZ-Yatsyshyn.doc

Скачиваний:

Добавлен:

01.05.2025

Размер:

2.34 Mб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

Івано-Франківський національний технічний

університет нафти і газу

Кафедра програмного забезпечення автоматизованих систем

М.М. Яцишин

МЕТОДИ ТА ЗАСОБИ ОБРОБКИ ЗНАНЬ У НАФТОГАЗОВІЙ ПРОМИСЛОВОСТІ

ЛАБОРАТОРНИЙ ПРАКТИКУМ

Для студентів напрямів підготовки

6.080403 – "Програмне забезпечення

автоматизованих систем",

6.050103 – "Програмна інженерія"

Рекомендовано методичною радою

університету

Івано-Франківськ

2012

Івано-Франківський національний технічний

університет нафти і газу

М.М. Яцишин

МЕТОДИ ТА ЗАСОБИ ОБРОБКИ ЗНАНЬ У НАФТОГАЗОВІЙ ПРОМИСЛОВОСТІ

ЛАБОРАТОРНИЙ ПРАКТИКУМ

Івано-Франківськ

2012

МВ 02070855-2690-2010

Яцишин М.М. Методи та засоби обробки знань у нафтогазовій промисловості: Лабораторний практикум. Івано-Франківськ: - ІФНТУНГ, 2012. – 60 с.

Лабораторний практикум розроблено відповідно до навчального плану та робочої програми дисципліни " Методи та засоби обробки знань у нафтогазовій промисловості ".

Містить теоретичні відомості до виконання лабораторних робіт та варіанти завдань.

Призначено для підготовки бакалаврів за напрямами: 6.080403 – "Програмне забезпечення автоматизованих систем", 6.050103 – "Програмна інженерія".

Рецензент: доктор технічних наук, професор кафедри інформатики

ІФНТУНГ Д.Ф. Тимків

Завідувач кафедри

програмного забезпечення

автоматизованих систем В.М. Юрчишин

Голова-навчально-методичного

об’єднана спеціальності В.М. Юрчишин

Коректор Н.Ф. Будуйкевич

Член експертно-рецензійної комісії М.Й. Федорів

Нормоконтролер Г.Я. Онуфрик

Інженер І категорії Н.В. Мирка

Рекомендовано методичною радою університету

(протокол № ____ від ______ 2012 р.)

МВ 02070855-2690-2012

Яцишин М.М., Юрчишин В.М. Методи та засоби обробки знань у нафтогазовій промисловості. Івано-Франківськ: - ІФНТУНГ, 2012. – 47 с.

Містить теоретичні відомості до виконання лабораторних робіт та варіанти завдань.

Рецензент: професор, зав. кафедри інформатики ІФНТУНГ

Тимків Д.Ф.

Рекомендовано методичною радою університету

(протокол №____ від ______ 2012 р.)

ЗМІСТ

ВСТУП 6

Лабораторна робота № 1-2. 7

Лабораторна робота № 3-4. 22

Лабораторна робота №5-6. 38

ДОДАТОК 50

СПИСОК ЛІТЕРАТУРИ 61

Вступ Лабораторна робота № 1-2.

Тема: Прямі методи прийняття рішень.

Мета: Ознайомитися із прямими методами прийняття рішень.

Завдання (варіант завдання для індивідуального виконання згідно виданого викладачем):

Знайти оптимальний варіант прийняття рішення.

Альтернатива 1 3.110 1.660 0.600 0.920

Альтернатива 2 1.650 3.510 0.780 2.570

Альтернатива 3 0.600 0.780 1.870 1.650

Вимоги до оформлення звіту:

Тема лабораторної роботи
Мета лабораторної роботи
Теоретичні відомості
Алгоритм описаних методів
Програмний продукт
Результати роботи створеного програмного продукту

Хід роботи

1. Використовується метод Лапласа.

Обчислення здійснюється за формулою .

Альтернатива із найбільшим середнім арифметичним значенням вважається найкориснішою.

Метод Лапласа
Порядок Альтернатива	Вибір1	Вибір 2	Вибір3	Вибір 4	Kl
1	3,11	1,66	0,66	0,92	1,59
2	1,65	3,51	0,78	2,57	2,13
3	0,60	0,78	1,87	1,65	1,23
max= 2,13

2. Застосовується метод Вальда (максимінний), при цьому використовується формула .

Метод Вальда
Порядок Альтернатива	Вибір1	Вибір 2	Вибір3	Вибір 4	Kv
1	3,11	1,66	0,66	0,92	0,66
2	1,65	3,51	0,78	2,57	0,78
3	0,60	0,78	1,87	1,65	0,60
min=0,78

3. Використовується метод Свіджа (метод мінімального ризику, де застосовується формула: .

Записуємо матрицю і знаходимо максимальні значення по рядках (MAX qij):

Метод Севіджа
Порядок Альтернатива	Вибір1	Вибір 2	Вибір3	Вибір 4	MAX qij
1	3,11	1,66	0,66	0,92	3,11
2	1,65	3,51	0,78	2,57	3,51
3	0,60	0,78	1,87	1,65	1,87

Будуємо матрицю ризиків ( )

	Матриця ризиків
Порядок Альтернатива		Вибір1	Вибір 2	Вибір3	Вибір 4	Ks
1	0,00	1,45	2,45	2,19	2,19	2,45
2	1,86	0,00	2,73	0,94	0,94	2,73
3	1,27	1,09	0,00	0,22	0,22	1,27
min=1,27

4. Метод компромісу Гурвіца.

Використовується формула :

Метод компромісу Гурвіца
Порядок Альтернатива	Вибір1	Вибір 2	Вибір3	Вибір 4	K mk
1	3,11	1,66	0,66	0,92	1,89
2	1,65	3,51	0,78	2,57	2,15
3	0,60	0,78	1,87	1,65	1,24

max ij	3,51
min ij	0,60

5. Метод половинного компромісу ризиків.

Використана формула - .

Метод половинного компромісу ризиків
Порядок Альтернатива	Вибір1	Вибір 2	Вибір3	Вибір 4	max
1	3,11	1,66	0,66	0,92	3,11
2	1,65	3,51	0,78	2,57	3,51
3	0,60	0,78	1,87	1,65	1,87

До даної матриці будуємо матрицю ризиків і проводимо обчислення за вищенаведеною формулою.

Матриця ризиків
Порядок Альтернатива	Вибір1	Вибір 2	Вибір 3	Вибір 4	Kmr
1	0,00	1,45	2,45	2,19	1,23
2	1,86	0,00	2,73	0,94	1,37
3	1,27	1,09	0,00	0,22	0,64
min=0,64

Виконання:

На основі описаних алгоритмів розрахунку за цими методами створено програмні продукти.

Метод Лапласа

#pragma endregion

private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {

double a[4],b[4],c[4],k[3],m;

double f(double h[],int n);

double g(double h[],int n);

a[0]=Convert::ToDouble(textBox4->Text);

a[1]=Convert::ToDouble(textBox7->Text);

a[2]=Convert::ToDouble(textBox10->Text);

a[3]=Convert::ToDouble(textBox13->Text);

b[0]=Convert::ToDouble(textBox5->Text);

b[1]=Convert::ToDouble(textBox8->Text);

b[2]=Convert::ToDouble(textBox11->Text);

b[3]=Convert::ToDouble(textBox14->Text);

c[0]=Convert::ToDouble(textBox6->Text);

c[1]=Convert::ToDouble(textBox9->Text);

c[2]=Convert::ToDouble(textBox12->Text);

c[3]=Convert::ToDouble(textBox15->Text);

k[0]=f(a,4);

k[1]=f(b,4);

k[2]=f(c,4);

m=g(k,3);

textBox16->Text=textBox16->Text+Convert::ToDouble(k[0]);

textBox17->Text=textBox17->Text+Convert::ToDouble(k[1]);

textBox18->Text=textBox18->Text+Convert::ToDouble(k[2]);

textBox19->Text=textBox19->Text+Convert::ToDouble(m);

}

private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {

this->Close();

}

};

}

double f(double h[],int n)

{

double d,S=0;

int i;

for(i=0;i<n;i++)

S+=h[i];

d=S/n;

return d;

}

double g(double h[],int n)

{

double max;

int i;

max=h[0];

for(i=0;i<n;i++)

{

if(h[i]>max)

max=h[i];

}

return max;}

Результати:

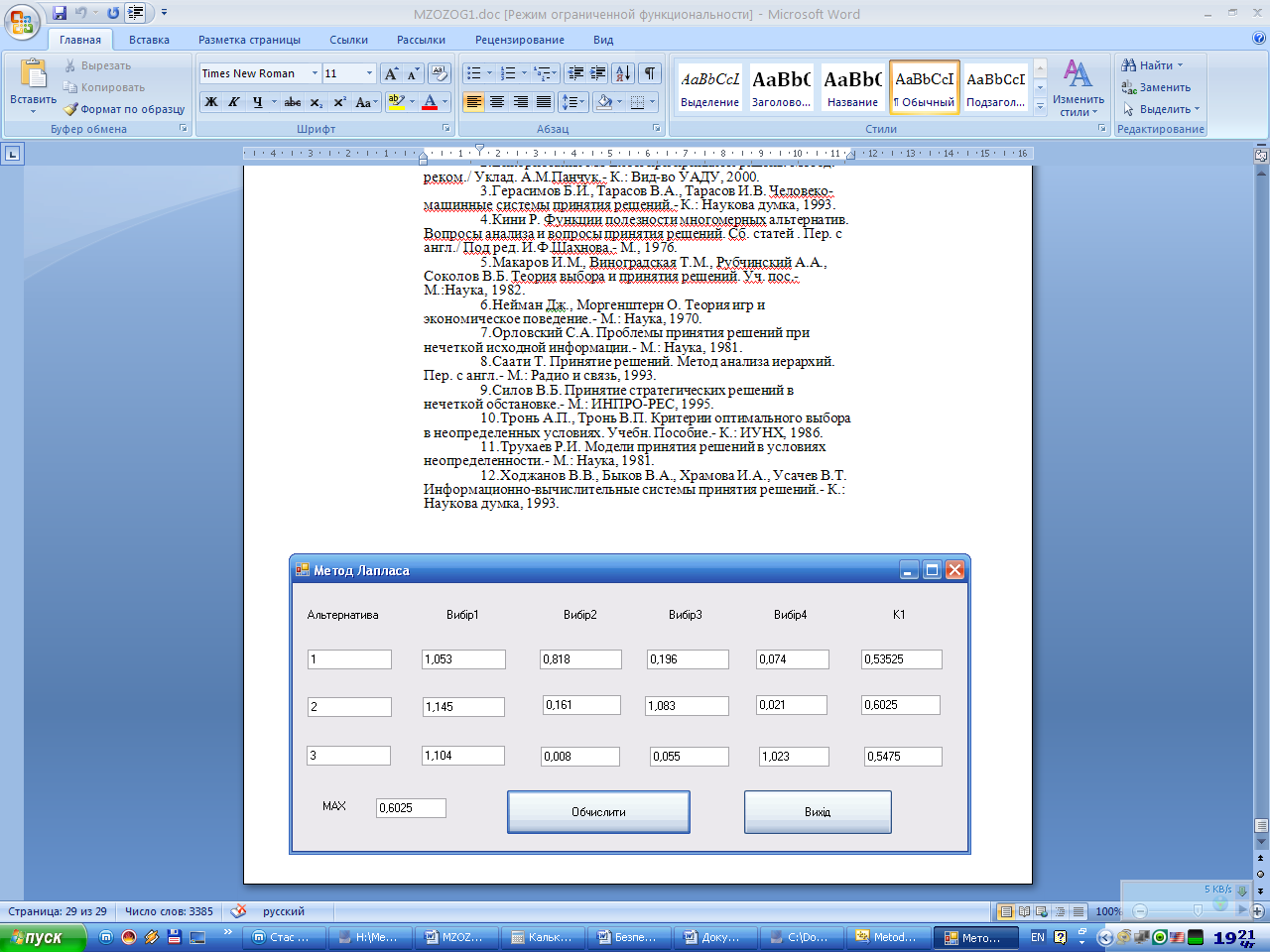
Метод вальда

…

#pragma endregion

private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {

double a[4],b[4],c[4],k[3],m;

double f(double h[],int n);

double g(double h[],int n);

a[0]=Convert::ToDouble(textBox2->Text);

a[1]=Convert::ToDouble(textBox3->Text);

a[2]=Convert::ToDouble(textBox4->Text);

a[3]=Convert::ToDouble(textBox5->Text);

b[0]=Convert::ToDouble(textBox8->Text);

b[1]=Convert::ToDouble(textBox9->Text);

b[2]=Convert::ToDouble(textBox10->Text);

b[3]=Convert::ToDouble(textBox11->Text);

c[0]=Convert::ToDouble(textBox14->Text);

c[1]=Convert::ToDouble(textBox15->Text);

c[2]=Convert::ToDouble(textBox16->Text);

c[3]=Convert::ToDouble(textBox17->Text);

k[0]=f(a,4);

k[1]=f(b,4);

k[2]=f(c,4);

m=g(k,3);

textBox6->Text=textBox6->Text+Convert::ToDouble(k[0]);

textBox12->Text=textBox12->Text+Convert::ToDouble(k[1]);

textBox18->Text=textBox18->Text+Convert::ToDouble(k[2]);

textBox19->Text=textBox19->Text+Convert::ToDouble(m);

}

private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {

this->Close();

}

};

}

double f(double h[],int n)

{

double min;

int i;

min=h[0];

for(i=0;i<n;i++)

{

if(h[i]<min)

min=h[i];

}

return min;

}

double g(double h[],int n)

{

double max;

int i;

max=h[0];

for(i=0;i<n;i++)

{

if(h[i]>max)

max=h[i];

}

return max;

}

Результати:

Метод Свіджа

…

#pragma endregion

private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {

double a[4],b[4],c[4],k[3],m,max[3];

double f(double h[],int n);

double g(double h[],int n);

a[0]=Convert::ToDouble(textBox2->Text);

a[1]=Convert::ToDouble(textBox3->Text);

a[2]=Convert::ToDouble(textBox4->Text);

a[3]=Convert::ToDouble(textBox5->Text);

b[0]=Convert::ToDouble(textBox8->Text);

b[1]=Convert::ToDouble(textBox9->Text);

b[2]=Convert::ToDouble(textBox10->Text);

b[3]=Convert::ToDouble(textBox11->Text);

c[0]=Convert::ToDouble(textBox14->Text);

c[1]=Convert::ToDouble(textBox15->Text);

c[2]=Convert::ToDouble(textBox16->Text);

c[3]=Convert::ToDouble(textBox17->Text);

max[0]=f(a,4);

max[1]=f(b,4);

max[2]=f(c,4);

for(int i=0;i<4;i++)

{

a[i]=abs(a[i]-max[0]);

b[i]=abs(b[i]-max[1]);

c[i]=abs(c[i]-max[2]);

}

k[0]=f(a,4);

k[1]=f(b,4);

k[2]=f(c,4);

m=g(k,3);

textBox6->Text=textBox6->Text+Convert::ToDouble(k[0]);

textBox12->Text=textBox12->Text+Convert::ToDouble(k[1]);

textBox18->Text=textBox18->Text+Convert::ToDouble(k[2]);

textBox19->Text=textBox19->Text+Convert::ToDouble(m);

}

private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {

this->Close();

}

};

}

double g(double h[],int n)

{

double min;

int i;

min=h[0];

for(i=0;i<n;i++)

{

if(h[i]<min)

min=h[i];

}

return min;

}

double f(double h[],int n)

{

double max;

int i;

max=h[0];

for(i=0;i<n;i++)

{

if(h[i]>max)

max=h[i];

}

return max;

}

результати:

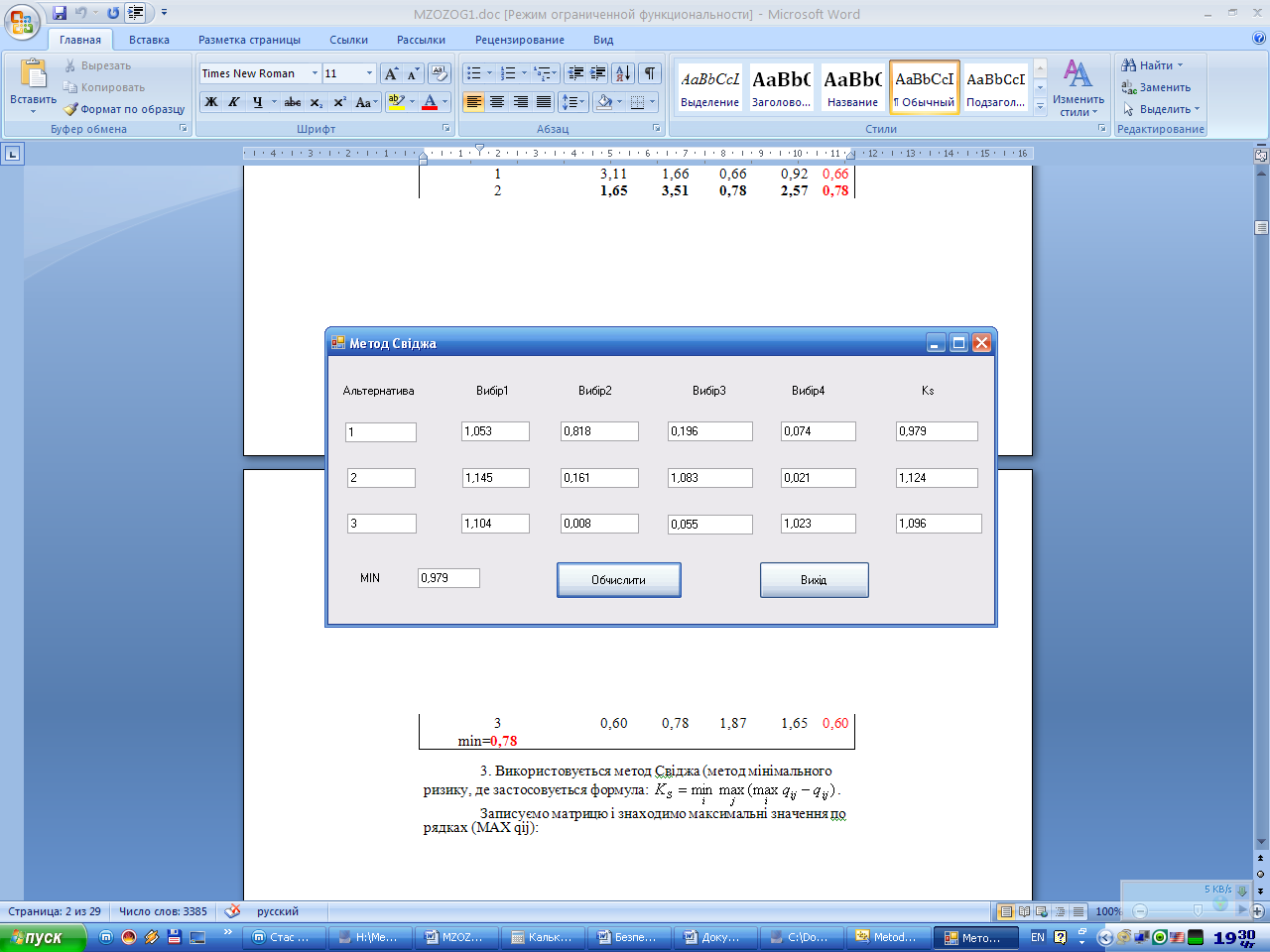
Метод компромісу Гурвіца

…

#pragma endregion

private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {

double a[4],b[4],c[4],k[3],k1[3],k2[3],min,max,s[12];

int j=0;

double f(double h[],int n);

double g(double h[],int n);

a[0]=Convert::ToDouble(textBox2->Text);

a[1]=Convert::ToDouble(textBox3->Text);

a[2]=Convert::ToDouble(textBox4->Text);

a[3]=Convert::ToDouble(textBox5->Text);

b[0]=Convert::ToDouble(textBox8->Text);

b[1]=Convert::ToDouble(textBox9->Text);

b[2]=Convert::ToDouble(textBox10->Text);

b[3]=Convert::ToDouble(textBox11->Text);

c[0]=Convert::ToDouble(textBox14->Text);

c[1]=Convert::ToDouble(textBox15->Text);

c[2]=Convert::ToDouble(textBox16->Text);

c[3]=Convert::ToDouble(textBox17->Text);

k1[0]=f(a,4);

k1[1]=f(b,4);

k1[2]=f(c,4);

k2[0]=g(a,4);

k2[1]=g(b,4);

k2[2]=g(c,4);

for(int i=0;i<3;i++)

k[i]=(k1[i]+k2[i])/2;

textBox6->Text=textBox6->Text+Convert::ToDouble(k[0]);

textBox12->Text=textBox12->Text+Convert::ToDouble(k[1]);

textBox18->Text=textBox18->Text+Convert::ToDouble(k[2]);

for(int i=0;i<4;i++)

{

s[j]=a[i];

j++;

}

for(int i=0;i<4;i++)

{

s[j]=b[i];

j++;

}

for(int i=0;i<4;i++)

{

s[j]=c[i];

j++;

}

min=g(s,12);

max=f(s,12);

textBox19->Text=textBox19->Text+Convert::ToDouble(min);

textBox20->Text=textBox20->Text+Convert::ToDouble(max);

}

private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {

this->Close();

}

};

}

double g(double h[],int n)

{

double min;

int i;

min=h[0];

for(i=0;i<n;i++)

{

if(h[i]<min)

min=h[i];

}

return min;

}

double f(double h[],int n)

{

double max;

int i;

max=h[0];

for(i=0;i<n;i++)

{

if(h[i]>max)

max=h[i];

}

return max;

}

Результати:

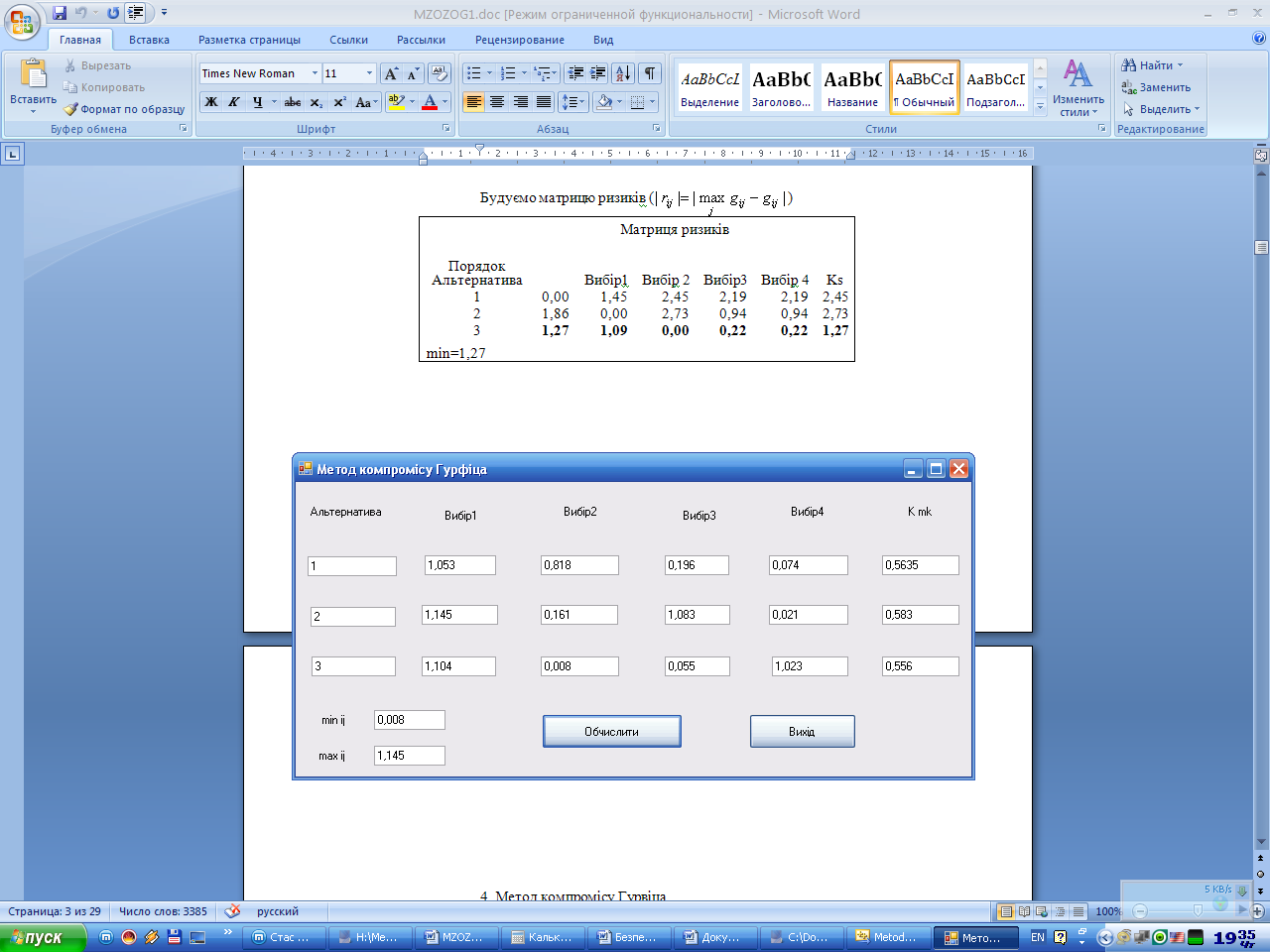
Метод половинного компромісу ризиків

…

#pragma endregion

private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {

double a[4],b[4],c[4],k[3],m,max[3];

double f(double h[],int n);

double g(double h[],int n);

a[0]=Convert::ToDouble(textBox2->Text);

a[1]=Convert::ToDouble(textBox3->Text);

a[2]=Convert::ToDouble(textBox4->Text);

a[3]=Convert::ToDouble(textBox5->Text);

b[0]=Convert::ToDouble(textBox8->Text);

b[1]=Convert::ToDouble(textBox9->Text);

b[2]=Convert::ToDouble(textBox10->Text);

b[3]=Convert::ToDouble(textBox11->Text);

c[0]=Convert::ToDouble(textBox14->Text);

c[1]=Convert::ToDouble(textBox15->Text);

c[2]=Convert::ToDouble(textBox16->Text);

c[3]=Convert::ToDouble(textBox17->Text);

max[0]=f(a,4);

max[1]=f(b,4);

max[2]=f(c,4);

for(int i=0;i<4;i++)

{

a[i]=abs(a[i]-max[0]);

b[i]=abs(b[i]-max[1]);

c[i]=abs(c[i]-max[2]);

}

max[0]=f(a,4);

max[1]=f(b,4);

max[2]=f(c,4);

k[0]=max[0]/2;

k[1]=max[1]/2;

k[2]=max[2]/2;

m=g(k,3);

textBox6->Text=textBox6->Text+Convert::ToDouble(k[0]);

textBox12->Text=textBox12->Text+Convert::ToDouble(k[1]);

textBox18->Text=textBox18->Text+Convert::ToDouble(k[2]);

textBox19->Text=textBox19->Text+Convert::ToDouble(m);

}

private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {

this->Close();

}

};

}

double g(double h[],int n)

{

double min;

int i;

min=h[0];

for(i=0;i<n;i++)

{

if(h[i]<min)

min=h[i];

}

return min;

}

double f(double h[],int n)

{

double max;

int i;

max=h[0];

for(i=0;i<n;i++)

{

if(h[i]>max)

max=h[i];

}

return max;

}

Результати:

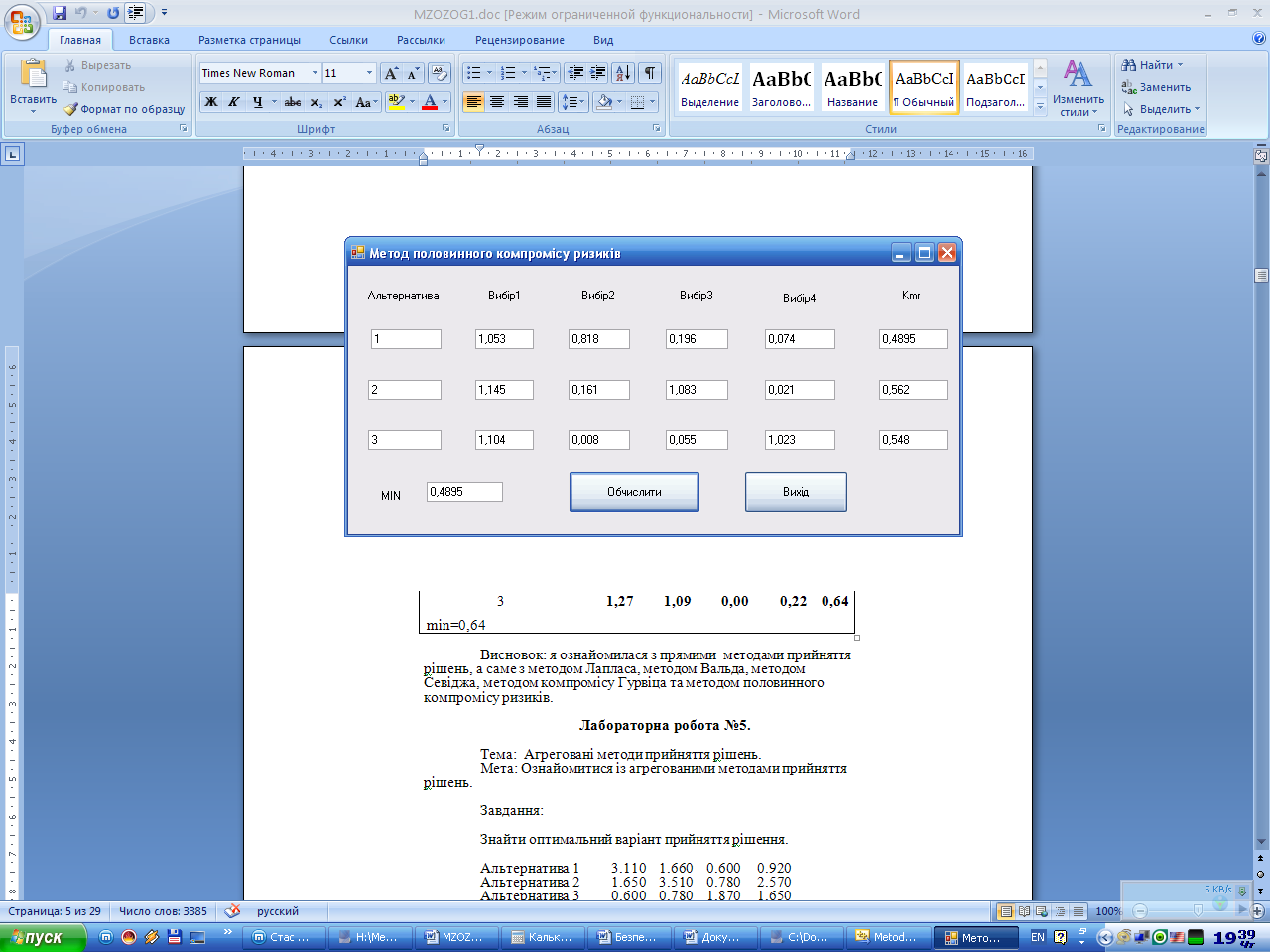
Виконуючи дану лабораторну роботу, студенти ознайомились із прямими методами прийняття рішень: метод Лапласа, метод Вальда, метод Свіджа, метод компромісу Гурвіца та метод половинного компромісу ризиків.

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.2025647.68 Кб0MO_ekzamen.doc
#
27.11.2019790.53 Кб5MO_redagovan_1-4 (2).doc
#
01.03.2025237.06 Кб0MR_MN_control.doc
#
21.11.2019245.76 Кб2MR_strategiyi.doc
#
01.05.2025335.24 Кб0MR_vid_A_do_Ya.docx
#
01.05.20252.34 Mб0MTZ-Yatsyshyn.doc
#
01.03.2025194.05 Кб0MZV_testi.doc
#
01.04.20252.07 Mб0n1.doc
#
01.04.2025123.9 Кб0narodni_pisni_dlya_nezalezhnogo.doc
#
23.11.2019354.3 Кб1Natsio_z_vidpov.doc
#
23.11.2019271.87 Кб1nats_onalna_eko_nom_ka1.doc