23

Министерство образования и науки Российской Федерации

ФГБОУ ВПО СахГУ

МОР

2012

Южно-Сахалинск

Содержание

Предисловие…………………………………………………………………….4

Основные вопросы курса…………………………………………………........4

1. Симплексный метод в линейном программировании…………..5

2. Двойственность в линейном программировании………………12

3. Транспортная задача……………………………………………..14

4. Сетевое планирование и управление. Расчёт основных показателей……………………………………………18

5. Элементы теории игр…………………………………………..

Библиографический список…………………………………………………..24

Предисловие

Пособие предназначено для студентов экономических специальностей. Перед решением задач, необходимо изучить теоретический материал по соответствующему разделу и разобрать решения типовых задач.

Содержание курса

1. Система m линейных уравнений с n неизвестными; базисные и свободные переменные; понятие базисного решения. Методы Крамера, матричный метод и Жордана – Гаусса.

2. Задача о выпуске продукции при условии полного использования сырья, задача о диете, транспортная задача). Задача линейного программирования.

3.Задача линейного программирования. Понятие о выпуклых множествах. Множество допустимых решений систем линейных уравнений и неравенств. Экстремум целевой функции. Графический метод.

4. Симплексный метод решения задачи ЛП.

5.Двойственность в линейном программировании. Двойственная задача к стандартной и основной. Основная теорема двойственности. Теорема равновесия. Экономическая интерпретация двойственных переменных.

6. Транспортная задача. Разрешимость транспортной задачи. Методы построения исходного допустимого плана. Метод потенциалов.

7. Сетевое планирование и управление. Сетевые графики, основные показатели. Метод критического пути.

8. Элементы теории игр.

1. Симплексный метод в линейном программировании

Рассмотрим математическую модель стандартной задачи линейного программирования (система ограничений содержит знаки неравенств).

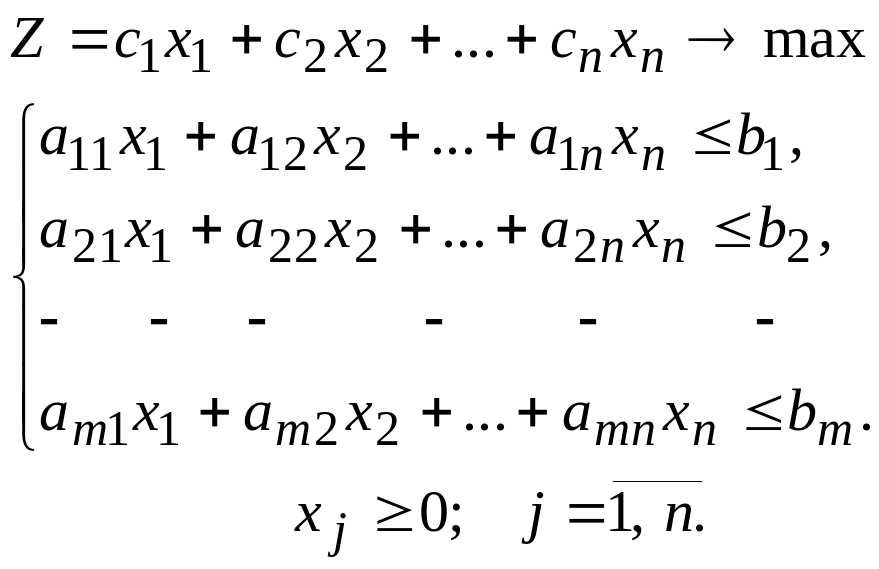(1)

Предположим, что все свободные члены b_i системы неотрицательны. Приведём систему к основной, добавив в левые части неотрицательные балансовые переменные X_n+1, …,X_n+m.

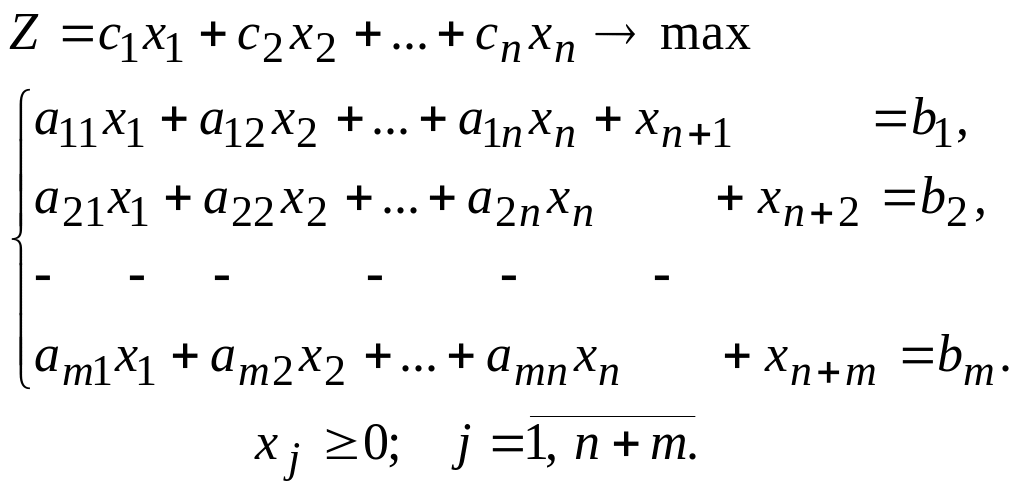(2)

Система ограничений в задаче (2) является канонической, т.к. она является системой с базисом и все её свободные члены неотрицательны. Такой системе соответствует опорное решение (базисное неотрицательное) =(0, 0, …,0, b₁, b₂, …, b_m), в котором все свободные неизвестные x_1, x₂, …, x_n равны нулю, а базисные x_n+1, x_n+2,…, x_n+m равны соответствующим свободным членам b₁, b₂, …, b_m.

Симплексный метод – это метод последовательного улучшения опорного решения. Задача решается в симплексных таблицах.

		0	С1	С2		Сn	0	0		0
Ci	Баз	bi	x1	x2	…	xn	xn+1	xn+2	…	xn+m	Ө
0	xn+1	b1	a11	a12	…	a1n	1	0	…	0
0	xn+2	b2	a21	a22	…	a2n	0	1	…	0
-	-	-	-	-	-	-	-	-	-	-
0	xn+m	bm	am1	am2	…	amn	0	0	…	1
	Z	0	-C1	-C2		-Cn	0	0		0

Этой таблице соответствует опорное решение Х₀=(0, 0, …,0, b₁, b₂, …, b_m) и соответствующее ему значение целевой функции Z₀=0.

Последняя строка таблицы называется индексной

Условием оптимальности решения при Z→max является неотрицательность оценок . Симплексным методом решается каноническая задача линейного программирования, у которой система ограничений каноническая, а целевая функция Z выражена через свободные неизвестные.