3.1.1. Критерий Рауса-Гурвица

Из теории известно, что критерий сводится к составлению определителя Гурвица и определению положительности соответствующих миноров. Для АСР 1-ого и 2-ого порядка с ПИ регулятором (как в прямом контуре, так и в контуре обратной связи) характеристическое уравнение будет иметь вид:

,

а их определители:

.

Если поставить коэф-ты в соответствии с записью векторов в MATLAB, то к соответствующему индексу надо прибавить 1.

М.б. два варианта решения проблемы:

1. Из коэф-тов вектора составляется определитель в виде квадратной матрицы и вычисляются определители всех диагональных алгебраических дополнений, путем пошагового удаления последней строки и последнего столбца. Все они должны быть больше 0 (положительны).

Длина вектора определяется функцией length(Nvec), а определитель вычисляется финкцией det(mat).

2. Прямое сравнение коэффициентовтов. Для системы 1-ого порядка:

Для системы 2-ого порядка:

В результате получаем, что:

или

Откуда можно сделать вывод, что система управления устойчива.

3.1.2. Критерий Михайлова

Для того чтобы система была устойчива, необходимо и достаточно, чтобы при ее кривая Михайлова, начинаясь с положительной вещественной полуплоскости, последовательно обходила квадрантов в положительном направлении (против часовой стрелки). Следует отметить, что кривые Михайлова устойчивых систем не пересекают начало координат и уходят на в -ом квадранте.

Для использования этого критерия в характеристическом уравнении оператор Лапласа заменяется на , Вследствие чего получим уравнение годографа Михайлова:

.

Замена оператора Лапласа в системе MATLAB осуществляется с помощью цикла for.

Выделяя вещественную и мнимую части функциями real и imag, строим годограф Михайлова в координатах . Далее по графику считаем количество пересеченных квадрантов.

График, соответствующий критерию Михайлова приведен на рис. 6

В результате из графика видно, что годограф Михайлова пересекает 2(3) квадранта. Т.к. порядок характеристического уравнения системы для объекта 1(2) порядка равен 2(3), следовательно, согласно критерию михайлова мохно заключить, что система устолйчива.

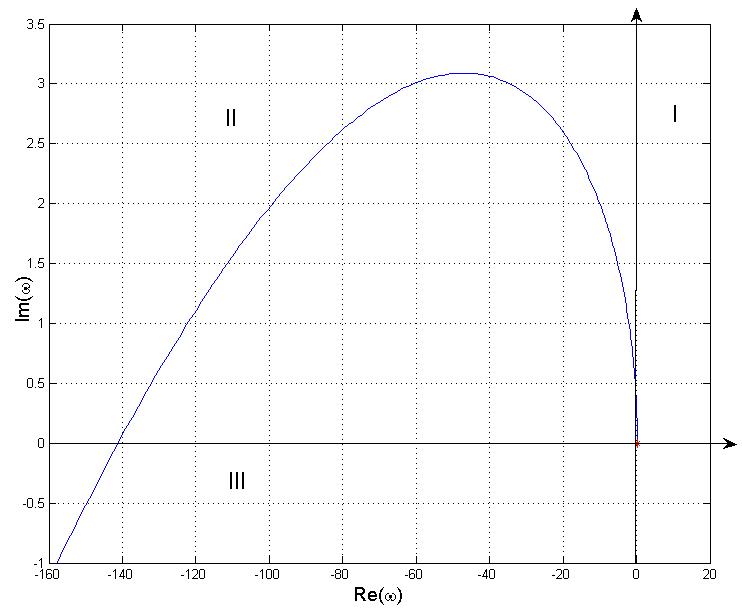
Рисунок 6. Годограф Михайлова

3.2. Критерий Найквиста

Критерий можно записать так: если кривая АФЧХ разомкнутой АСР не охватывает точку (–1; j0), то замкнутая АСР является устойчивой.

Поэтому, строим диаграмму Найквиста для системы с помощью функции Nyquist:

Nyquist(sysR*sysO), grid on

Диаграмма Найквиста представлена на рис. 7.

Из графика очевидно, что кривая не охватывает точку (–1; j0), сто соответствует устойчивости системы.

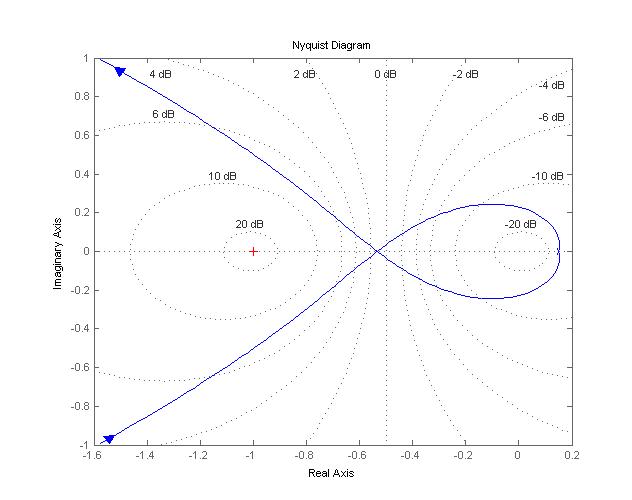
Рис. 7. Диаграмма Найквиста

4. Построение переходного процесса в аср.

Качество переходного процесса.

Переходной процесс – это изменение регулируемой величины во времени при переходе из одного установившегося состояния в другое.

Характер переходного процесса системы зависит от вида возмущающего воздействия и начальных условий. Для того, чтобы можно было сравнить между собой системы по характеру переходного процесса, из возможных воздействий выбирают типовые или наиболее неблагоприятные и определяют кривую переходного процесса при нулевых начальных условиях. В качестве типовых воздействий при анализе динамики АСР обычно используют единичное ступенчатое воздействие, единичный импульс, линейно возрастающее воздействие, синусоидальное воздействие и др. Для большинства систем типовым и наиболее неблагоприятным является воздействие вида единичной ступенчатой функции . Реакция системы на единичное ступенчатое воздействие при нулевых начальных условиях называется переходной функцией системы.

Переходная функция системы оценивается с помощью совокупности характеристик, называемых показателями качества переходного процесса. Обычно различают следующие показатели качества переходного процесса системы:

1. Динамическая ошибка регулирования – максимальное отклонение регулируемой величины. не должна превышать наперед заданного значения динамической ошибки ( ).

2. Статическая ошибка – это остаточное отклонение регулируемой величины от заданного значения. не должна превышать наперед заданного значения ( ).

3. Время регулирования или время переходного процесса – это время от начального изменения выходной величины до ее нового установившегося значения. Время регулирования характеризует быстроту затухания переходного процесса. В этом случае требуется минимизировать.

Одновременно соблюдать все требования к техническому процессу невозможно, поэтому в каждом конкретном случае за критерий оптимизации берется качество продукта, прибыль, производительность и т.д.

Передаточная функция замкнутой АСР:

.

где , .

С помощью функции step получаем значения векторов для времени (t) и h(t) и функцией plot строим график переходного процесса.

График переходного процесса АСР представлен на рисунке 8.

По полученному графику определяем параметры качества переходного процесса:

1. Динамическая ошибка .

2. Статическая ошибка .

3. Время регулирования .

4. Площадь под кривой S=____.

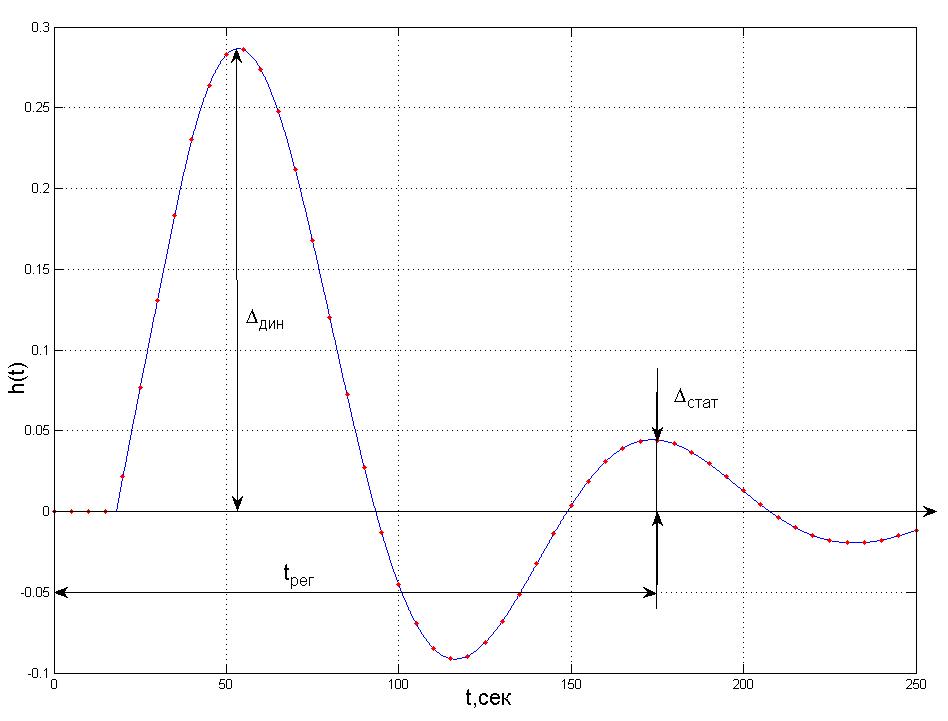
Рис. 8. Переходной процесс в АСР

Заключение

В данной работе в системе MATLAB при использовании пакета Control System Toolbox были проделаны следующие этапы исследования системы:

• определены динамические характеристики объекта:

    – переходная характеристика;

    – импульсная характеристика;

    – частотные характеристики (АЧХ, ФЧХ и АФЧХ).

• выбраны оптимальные параметры настройки ПИ регулятора,

• произведена проверка системы на устойчивость,

• построен переходной процесс и найдены его параметры качества.