1.2 Определение частотных характеристик объекта.
Важной характеристикой динамических звеньев и систем автоматического управления являются частотные характеристики. Достоинство методов исследования систем в частотной области состоит в том, что частотные характеристики позволяют просто выявить влияние того или иного параметра на динамические свойства системы (устойчивость, переходной процесс и т.д.). Кроме того, частотные характеристики можно получить экспериментально, что важно в тех случаях, когда трудно составить уравнения динамики (например, для систем с распределенными параметрами). Частотные характеристики звеньев и систем строятся на основании их комплексных передаточных функций.
Комплексной
передаточной функцией
называется отношение выходной величины,
преобразованной по Фурье, к входной
величине, преобразованной по Фурье в
режиме незатухающих гармонических
колебаний.
Амплитудно-частотной
характеристикой
(АЧХ) называется отношение амплитуды
выходного гармонического сигнала к
амплитуде входного гармонического
сигнала.
– это модуль комплексной передаточной
функции:
.
показывает, как данное звено пропускает сигнал на определенной частоте и оценка эта делается по отношению амплитуды выходной величины к амплитуде входной величины.
Фазо-частотной характеристикой (ФЧХ) называется разность между входными и выходными колебаниями:
.
показывает,
каков сдвиг по фазе между выходным и
входным сигналом на данной частоте:
.
В пакете Control System Toolbox построение АЧХ и ФЧХ реализовано посредством функции bode. для моделирования временного отклика систем. Функция bode возвращает диаграммы Боде – графики логарифмической амплитудно-частотной характеристики (ЛАЧХ) и логарифмической фазо-частотной характеристики (ЛФЧХ):
Функция impulse может быть записана в следующем виде:
bode(sys) или bode(sys,w)
bode(sysl,sys2,...,sysN) или bode(sysl,sys2,...,sysN,w)
bode(sysl,'PlotStylel',...,sysN,'PlotStyleN')
[mag,phase,w]=bode(sys)
Здесь аргумент w задает диапазон частот (w=[wmin,wmax] или w=[wmin:hw:wmax]), остальные аргументы – такие же, как у ранее рассмотренных функций step и impulse. Возвращаемые величины:
• диаграммы Боде для моделей с заданными именами;
• mag, phase, w – соответственно массивы значений амплитуд и фаз и вектор частот.
Как было сказано выше, функция bode непосредственно строит графики частотных характеристик в полулогарифмической плоскости по частоте – ЛАЧХ и ЛФЧХ. Для получения логарифмических характеристик в декартовых координатах (АЧХ и ФЧХ), с помощью функции bode возвращают вектора соответствующие амплитуде, фазе и частоте, соответственно. После чего строят графики зависимость амплитуды и фазы от частоты.
Графики АЧХ и ФЧХ представлены на рисунке 3.
Амплитудо-фазо-частотная
характеристика (АФЧХ)
представляет собой геометрическое
место точек на комплексной плоскости
концов вектора при изменении
от 0 до
.
Сам вектор – это модуль комплексной
передаточной функции или АЧХ, а угол
между этим вектором и положительной
вещественной осью – аргумент комплексной
передаточной функции или ФЧХ.
АФЧХ может быть
получено по передаточной функции путем
замены
.
После соответствующих преобразований
выделяют реальную (
)
и мнимую (
)
части. Для передаточной функции объекта
1(2)-ого порядка выражения для
и
в общем виде могут быть записаны следующим
образом:
|
;
.или
|
|
;
.
Подставляя численные значения объекта, получим:
|
|
;
.или
|
|
;
.Изменяя от 0 до выбранного значения, так, чтобы была очевидна точка сходимости, в редакторе М-файлов системы MATLAB можно ввести полученные выражения и построить параметрический график зависимости:
.
Отметим,
что получив выражения для
и
также можно построить графики для АЧХ
и ФЧХ (
и
).
Однако пакет Control System Toolbox предоставляет простое средство для построения АФЧХ. График АФЧХ можно получить с помощью функции nyquist, описание которой приведены ниже.
Функция nyquist возвращает диаграмму Найквиста (годограф):
nyquist(sys) или nyquist(sys,w)
nyquist(sysl,sys2,...,sysN) или nyquist(sysl,sys2,...,sysN,w)
nyquist(sysl,'PlotStylel',...,sysN,'PlotStyleN1)
[re,im,w]=nyquist(sys)[re,im]=nyquist(sys,w)
Аргументы этой функции аналогичны выше описанным функциям.
Возвращаемые величины:
• диаграмма Найквиста (в многомерном случае — для каждого канала вход/выход);
• re и im — соответственно векторы значений вещественной и мнимой частей комплексного коэффициента передачи для заданных частот.
Непосредственное использование функции nyquist приводит к построению зеркально отображенного графика с выводом сетки координат по частоте, что обусловлено использованием данной функции для исследования устойчивости систем, что будет показано ниже.
В нашем случае, используя функцию nyquist, возвращаем вектора, соответствующие значениям вещественной и мнимой части комплексной передаточной функции. Далее, как и для диаграмм Боде, через функцию plot строим соответствующий график для АФЧХ.
График приведен на рисунке 4.
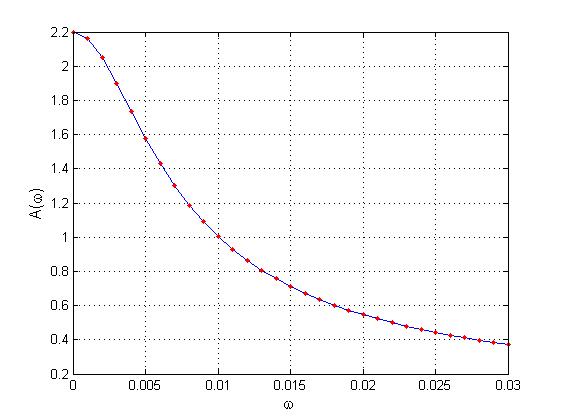
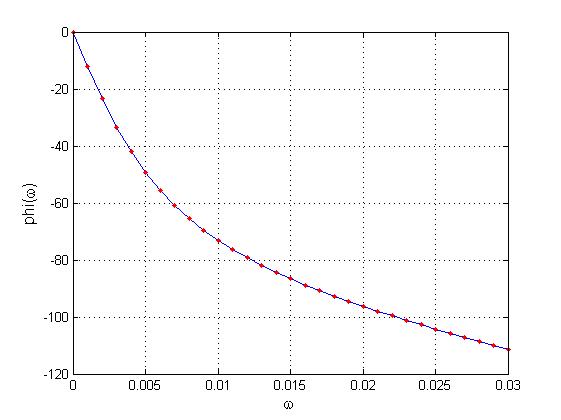
Рис. 3. Графики АЧХ
и ФЧХ
Рис. 3. График амплитудно-фазо-частотной характеристики