6. Определение дифференциального порога слуховой системы по методу констант графическим способом.

Вычисляются:

X_к – значение дифференциального порога по методу констант;

M – доверительный интервал (верхнее и нижнее значения) для значений количества проб в которых сигналы восприняты как неравные (f) в методе констант при доверительной вероятности β = 0.95. Значения доверительного интервала определяются в соответствии с таблицей «Приложение 1». При этом:

f – количество проб в которых сигналы восприняты как неравные (данные из протокола)

N – количество предъявлений проб сигналов с одной разностью интенсивностей стимулов (в нашем эксперименты N = 30)

Р_обн – вероятность обнаружения различия сигналов по громкости, вычисляется по формуле:

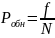
Результаты расчетов заносятся в табл. 6.1 и отображаются на рис. 6.1.

Таблица 6.1 Расчет вероятности обнаружения различия сигналов по громкости (P_обн) и значений доверительного интервала (M).

Количественные характеристики проб	Величина различия по громкости стандартных и переменных сигналов
	0	1	2	3	4	5	6
Количество проб, в которых сигналы восприняты как неравные; f	2	3	19	27	28	26	28
Вероятность обнаружения различия сигналов по громкости; Pобн	0.06	0.1	0.63	0.9	0.93	0.86	0.93
Доверительный интервал; М (верхнее и нижнее значения)	0,213	0,256	0,782	0,966	0,982	0,948	0,982
	0,018	0,034	0,455	0,744	0,787	0,703	0,787

Построение графика зависимости вероятности обнаружения различий в громкости стандартного и переменного сигналов (P_обн) от величины этого различия (∆I).

Как следует из графика Х_к=1,80

7. Статистическая обработка экспериментальных данных метода границ в координатах нормированного отклонения z.

Для уточнения значения дифференциального порога по методу констант и определения стандартного отклонения, производится «выпрямления» кривой вероятности обнаружения (рис.6.1) в координатах нормированного отклонения Z. Для этого по имеющимся значениям Р_обн (табл.6.1) в соответствии с таблицей «Приложение 2» определяются значения нормированного отклонения Z_oбн. Этими значениями, а также значениями, необходимыми для расчета параметров линейной зависимости заполняется Ta6лица 7.1.

Таблица 7.1 Сводная таблица значений нормированного отклонения Z, расчета параметров линейной зависимости и значений доверительного интервала в Z-единицах.

∆I	f	Pобн	Zобн	∆I*Zобн	∆I2	M	Zдов.инт
0	2	0.06	-1.55	0	0	0,213	-0,31
						0,018	-2,33
1	3	0.1	-1.28	-1.28	1	0,256	-0,67
						0,034	-1,88
2	19	0.63	0.33	0.66	4	0,784	-0,77
						0,455	-0,13
3	27	0.9	1.28	3.84	9	0,966	1,75
						0,744	0,64
4	28	0.93	1.48	5.92	16	0,982	2,05
						0,787	0,77
5	26	0.86	1.08	5.4	25	0,948	1,55
						0,703	0,52
6	28	0.93	1.48	8.88	36	0,982	2,05
						0,787	0,77
∑∆I = 21			∑Zобн = 2.82	∑∆I*Zобн = 23.42	∑∆I2 = 91

Для нахождения уравнения линейной зависимости решается системы линейных уравнений:

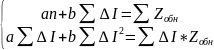
где: n – число различий в громкости стандартного и переменного сигналов (в нашем эксперименте n = 7);

a и b – параметры прямой;

значения ∑∆I, ∑Z_обн, ∑∆I², ∑∆I Z_обн - приведены в таблице 7.1.

Определив a и b, подставляем найденные значения в уравнение:

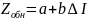
Решив данное уравнение, строим график прямо-пропорциональной зависимости Z_обн от ∆I.

Построение графика линейной зависимости нормированного отклонения (Z_обн) от величины различия по громкости стандартных и переменных сигналов (∆I) методом наименьших квадратов.