Метод ветвей и границ.

Метод ветвей и границ заключается в разбиении конечного множества, на котором ищется экстремум, на несколько подмножеств и в выяснении перспективности каждого из них. Если подмножество неперспективно, оно исключается из рассмотрения. Если в подмножестве может находиться экстремум, оно подвергается дальнейшему разбиению и исследованию. Разбиение и исследование продолжаются до тех пор, пока не будет выявлена единственная наилучшая точка. Исключение из рассмотрения неперспективных точек обуславливает направленность перебора. В большинстве задач дискретного программирования оценки перспективности подмножеств точек могут быть только приближенными. Если применяются излишне оптимистические оценки перспективности, перебор начинает приближаться к полному, увеличиваются потери на поиск. Если правила выбора перспективных ветвей излишне пессимистические, то снижается надежность определения экстремума.

Рассмотрим использование метода ветвей и границ для определения оптимальной последовательности фрезерования поверхностей.

Определение последовательности фрезерования отдельных поверхностей и их совокупностей является достаточно сложной задачей. Это обусловлено большим количеством факторов, влияющих на последовательность обработки и неясностью связей между факторами, затрудняющих выявление закономерностей построения последовательностей обработки.

Эту задачу трансформируем в задачу минимизации холостых перемещений инструмента. Такой подход возможен потому, что последовательность обработки будем искать в рамках установки, т.е. вопросы, связанные с определением поверхностей базирования и закрепления, решены.

Сокращение длины холостых перемещений является одним из резервов увеличения производительности труда. Под холостым перемещением понимается движение фрезы между двумя рабочими перемещениями. Одним рабочим перемещением может обрабатываться как одна, так и совокупность поверхностей (карман, колодец, контур) (рис. 3.2).

Все множество холостых перемещений для данной установки, имеющей n рабочих перемещений, можно представить в виде ориентированного графа _

G=(c, U),

у которого: с – множество вершин (множество рабочих перемещений); U – множество ориентированных дуг (наличие дуги указывает на возможность перемещения от одного рабочего перемещения к другому).

В реальных условиях граф G не является полным, так как существуют условия, запрещающие перемещения. К этим условиям можно отнести: расположение элементов базирующих и закрепляющих устройств; нежелательное изменение внутренних напряжений и перераспределение жесткости системы СПИД; выделение большого количества тепла, затрудняющего получение необходимой шероховатости и точности и т.д.

Задача минимизации холостых перемещений ставится в терминах дискретного программирования и формулируется следующим образом.

Минимизировать целевую функцию

n n

Σ Σ C_ij X_ij,

i=1 j=1

где С_ij=∞.

Через С_ij>0 обозначим расстояние между рабочими перемещениями i и j. С_ij=∞, если «прямого» маршрута между перемещениями i и j не существует. В некоторых случаях С_ij≠С_ji, т.е. начало обработки не совпадает с окончанием.

Булевы, перемещенные X_ij, определяются следующим образом:

I, если цикл включает холостое перемещение от рабочего перемещения i к j ;

0, в противном случае.

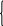
X_ij=

Переменные удовлетворяют условиям:

, i є {1,2,…,n} (отход)

, j є {1,2,…,n} (подход)

X_ij – неотрицательные целые при любых i и j.

Решение-цикл

Условие С_ii=∞ принимается для того, чтобы исключить возможность появления в оптимальном решении значений X_ii=I, не имеющих смысла.

Наилучшие результаты при решении поставленной задачи были получены при использовании метода ветвей и границ.

Существует несколько модификаций метода ветвей и границ. Здесь рассмотрим метод «задания маршрутов», так как для его применения нет необходимости решать предварительную задачу линейного программирования о назначениях. Для определения нижней оценки оптимального значения целевой функции применяется метод, основанный на том, что расстояние должно быть, по крайней мере, равно сумме C_ij при X_ij=1 плюс сумма наименьших C_ij в остальных случаях.

Алгоритм определения оптимального цикла, реалиизующий метод задания маршрутов, имеет вид: Сформировать список задач и для каждой задачи из этого списка проделать следующие шаги.

Шаг 1.

Прекратить вычисления, если основной список пуст. В противном случае выбрать одну задачу и вычеркнуть ее из основного списка.

Шаг 2.

Определить нижнюю оценку целевой функции для любого цикла, порождаемого выбранной задачей. Если же нижняя оценка больше или равна X₀^t, то принять X₀^t+1 и вернуться к шагу 1. В противном случае перейти к шагу 3.

Шаг 3.

Если текущее решение определяет цикл, то зафиксировать его, принять X₀^t+1 равным соответствующему значению целевой функции и вернуться к шагу 1. В противном случае перейти к шагу 4.

Шаг 4.

При наличии возможности выбрать переменную Х_hk, не входящую в текущее решение, такую, что С_hk<∞ при условии, что Х_hk=1 не приводит к образованию подцикла на переменных, уже вошедших в решение. При таком выборе внести в основной список задач две задачи.

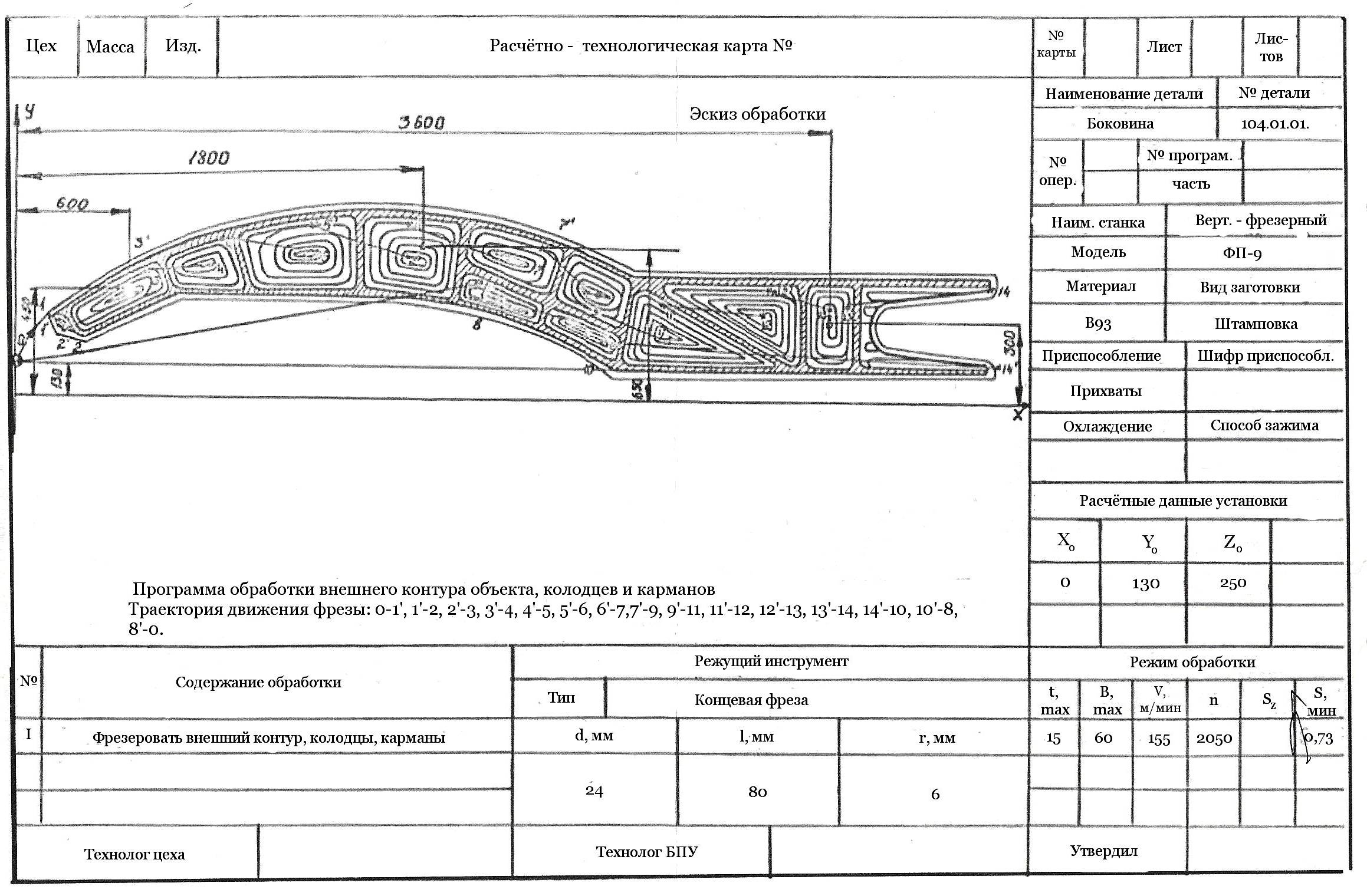Рис. 3.17.

Каждую из этих задач принять идентичной задаче, выбранной на шаге 1, за исключением лишь того, что в одну из них ввести изменение С_hk=∞, а в другую – условие Х_hk=1 и изменение С_kh=∞. Принять X₀^t+1= X₀^t и вернуться к шагу 1.

По приведенному алгоритму была составлена программа и проведен ряд экспериментов на электронно-вычислительной машине. Результаты экспериментов показали большую эффективность программы в смысле нахождения оптимального цикла, но при этом очень быстро возрастает время счета с увеличением размерности задачи.

На рис. 3.17 представлена траектория, сформированная с помощью этого алгоритма, для изображенной детали.