5. Методы, алгоритмы оптимального проектирования.

   1. Постановка задачи классификации объектов.

Пусть S (D) - универсальное множество объектов классификации,d_i-элемент этого множества, т.е. d_i Є S(D). Ŝ - множество объектов, принадлежащих классификации в данный момент. Очевидно, Ŝ принадлежит S(D).

Классификация элементов множества Ŝ сводится к разбиению его на систему пересекающихся подмножеств S = {S₁,S₂,....S_N}. Таким образом, чтобы удовлетворились аксиомы разбиения:

• S_i Є Ŝ

• S_i ≠ Ǿ, γ i Є 1,N

• S_i ∩ S_j =Ǿ, γ( i≠j)

• Ũ S_i = Ŝ

Множество S делимо по признаку p, если имеются элементы, обладающие этим признаком, т.е. Ξ d_i Є S^p Є S, где S^p- множество элементов, обладающих признаком p.

Объект классификации di обладает признаком классификации р, если находиться в отношении d_ipd_j к объекту d_j (типовой объект классифицируемой группы). Все элементы множества S, обладающие признаком р, составляют отдельный класс S^P_K Є Ŝ, а отношение р, определяющие признак деления, является отношением эквивалентности на множестве S, т.е.

• d_ipd_j → d_i = d_j

• d_ipd_j ↔ d_ipd_j

• (d_ipd_j) Λ (d_ipd_k)→ d_ipd_k

При рассмотрении деталей как объектов классификации различают их между собой по совокупности конструктивно-технологических признаков: габаритные размеры, типы поверхностей, материалы, шероховатость поверхностей и т.д.

Используя эти признаки можно составить описание детали:

υ (d_i) = <p₁, p₂, ....,p_m>, m≤l

( l –общее количество признаков).

Множество всех возможных описаний V есть прямое декартово произведение:

V= M₁*M₂*....*M_n1

В этом случае описание объектов классификации равнозначно заданию функции f (функция измерения), отображающей S в пространство V

f: S→V

2. Алгоритмы формирования классификационных группировок.

Представим каждую деталь, как точку в n-мерном пространстве свойств. Тогда каждому классу деталей должна соответствовать особенная группа точек в этом пространстве. Для оценки меры близости между точками и группами точек им ставится в соответствие некоторая функция. Рассмотрим, например, функцию

f(R)= 1/(1+αR² ),

где α- коэффициент пропорциональности,

R- расстояние между точками в пространстве.

За R примем так называемое расстояние по Хеммингу, равное числу несовпадающих координат обеих точек. Величина f считается мерой близости, пропор-циональной расстоянию R.

Таким образом, мера близости между точками a₂ и a₁ равняется

F( a_2, a₁)= 1/(1+αR²( a_2, a₁ ))

А средняя мера близости между точкой а и множеством точек А, равняется:

f(a,A)= (1/N_A )*∑f (A,a_i)

где N_A – количество точек множества А.

Аналогично вводится мера близости между двумя множествами точек А и В:

f(A,B)=( 1/N_A)* ∑f (a_i, B )

или

f(B,A)=( 1/N_b)* ∑f (A,b_j,)

Рассмотрим пример. Пусть имеются две детали, векторы которых в пространстве свойств соответственно равны

F (a₁)=[10100] и F(a₂)=[00010]

Определим разности (число несовпадающих координат)

F (a₁)=[10100]

F(a₂)=[00010]

F (a₁)- F(a₂)=[10110]

Расстояние R определяется как сумма значений компонентов вектора F (a₁)- F(a₂),т.е. R=1+0+1+1+0=3, а мера близости

f(a₁,a₂)=1/(1+[1/5² ]*3² ) = 0,74

где α= 1/5² - коэффициент, учитывающий общее количество свойств.

При реализации алгоритмов классификации объекты могут предъявляться на классификацию либо последовательно, один за другим, либо параллельно. Последовательные алгоритмы классификации применяются тогда, когда неизвестно заранее число деталей, подлежащих классификации.

Алгоритм 1.

Исходные данные А=(а₁,......,а_N)- последовательно вводимые детали; [1]- допустимая мера близости.

1.Первая деталь а₁ принудительно относится к первому классу

К₁ ={а₁}

F (a₃) = [11100]

F (a₄) = [10110]

F (a₁, a₂ , a₃ , a₄ )= [41411]; ∑=4+1+4+1+1=11

Среднее значение 11:5=2.2. тогда вектор типового представителя класса [a₁,a₂,a₃,a₄] имеет вид F(a* )=[10100]. В данном случае он совпадет с деталью a₂ .

Рассмотрим пример проведения классификации по предложенному ранее алгоритму 1. Детали, которые надо классифицировать представим на рис. 3.13

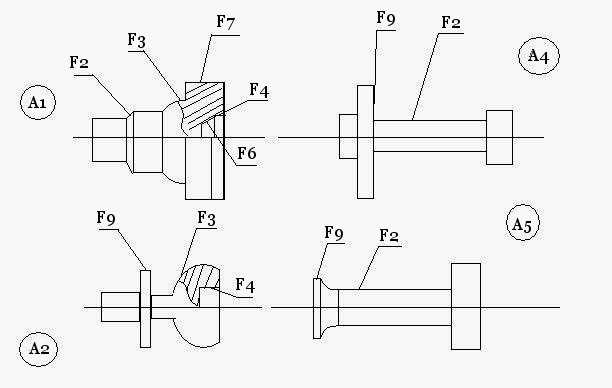
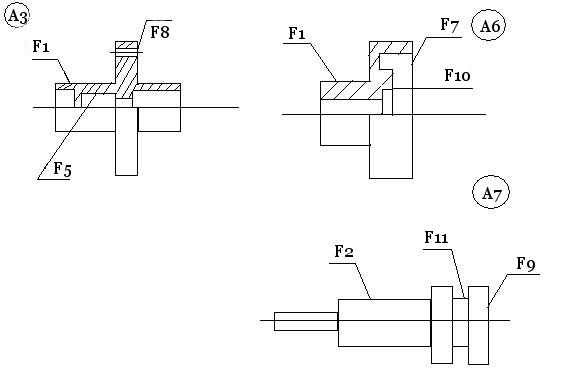
В таблице 3.3 представлено описание формы детали (упрощенно).

В качестве признаков выбраны типы поверхностей:

F_{1 -} цилиндрическая наружная гладкая

F₂ - цилиндрическая наружная ступенчатая

F₃ – сферическая наружная

F₄ - цилиндрическая внутренняя гладкая

F₅ - цилиндрическая внутренняя ступенчатая

F₆ – коническая внутренняя

F₇ – фланец

F₈ – фланец с отверстиями

F₉ - выступ наружный

F₁₀ – выступ внутренний

F₁₁-паз наружный

Таблица 3.3

	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11
F(A1)		1	1	1		1	1
F(A2)			1	1					1
F(A3)	1				1			1
F(A4)		1							1
F(A5)		1							1
F(A6)	1				1		1			1
F(A7)		1							1		1

Вычислим меру близости между детали a₁ и a₂. Выпишем векторы этих деталей:

F (a₁) = [01110110000]

F (a₂) = [00110000100]

F (a₁ a₂) = [01000110100]

R=0+1+0+0+0+1+1+0+1+0=4

f(a₁ a₂) =1/ (1+ [4 ² /11² ]) =0.885

Вычислим меры близости для остальных наружных деталей и сведем все это в матрицу (Таблица 3.4.)

Таблица 3.4

	a1	a2	a3	a4	a5	a6	a7
a1		0.88	0.66	0.83	0.83	0.71	0.77
a2			0.77	0.93	0.93	0.71	0.93
a3				0.83	0.83	0.93	0.77
a4					0.1	0.77	0.99
a5						0.77	0.99
a6							0.71
a7

Пусть порядок предъявления деталей на классификацию следующий

{a₁ a₂ a₃ a₄ a₅ a₆ a₇ }

Рассмотрим последовательность формирования классов при ограничении [1]=0.85

1.Первая деталь a₁ относится к первому классу K₁

K₁ ={ a₁ }

2. Вторая деталь a₂ относится к первому классу K₁ и вычисляется мера близости деталей a₁ и a₂ в классе

K₁ ={ a₁ a₂ }→ f(K₁}=0.88> [1]

3.Третья деталь a₃ относится к первому классу K₁ и вычисляется мера близости деталей a₁ a₂ a₃ в классе:

K₁ = { a₁ a₂ a₃ }→ f(K₁ )=0.66< [1]

В этом случае не выполняется условие f(K₁)≥[1], поэтому деталь a₃ образует класс K₂:

K₂={ a₃ }

4.Четвертая деталь a₄ относится последовательно к первому K₁ и ко второму K₂ классам меры близости:

K₁ ={ a₁ a₂ a₄ }→ f(K₁ )=0.83<[1]

K₂ ={ a₃ a₄ }→ f(K₂)=0.83<[1]

Условие f(К₁ )≥[1] не выполняется и поэтому четвертая образует новый класс K₃

K₃={ a₄ }

5.Пятая деталь a₅ относится последовательно к первому К₁ ,второму K₂ и третьему K₃ классам и вычисляются меры близости

K₁ ={ a₁ a₂ a₅ }→ f(K₁ )=0.83<[1]

K₂= { a₃ a₅ }→ f(K₂)=0.83< [1]

K₃ ={a₄ a₅ }→ f(K₃ )=1.0>[1]

По условию f(К₁ )≥[1] пятая деталь относится к третьему классу.

6.Шестая деталь a₆ относится последовательно к первому K₁, второму K₂ и третьему K₃ классам и вычисляются меры близости:

K₁ ={ a₁ a₂ a₆}→ f(K₁ )=0.71<[1]

K₂ ={ a₃ a₆ }→ f(K₂ )= 0.93>[1]

K₃ = { a₄ a₅ a₆ }→ f(K₃ )=0,77< [1]

7.Седьмая деталь a₇ относится последователь к первому K₁ ,второму K₂, третьему K₃ классам и вычисляется мера близости:

K₁ = { a₁ a₂ a₇}→ f(K₁ )=0.77<[1]

K₂ ={ a₃ a₆ a₇}→ f(K₂ )= 0.71<[1]

K₃ ={ a₄ a₅ a₇ }→ f(K₃ )=0,99>[1]

По условию f(К₁ )≥[1] седьмая деталь a₇ относится к третьему классу. Таким образом, получили следующие классы и меры близости деталей:

K₁ ={ a₁ a₂ }→ f(K₁ )=0.88

K₂ ={ a₃ a₆ }→ f(K₂ )= 0.93

K₃ ={ a₄ a₅ a₇ }→ f(K₃ )=0,99

Сформированный состав классов соответствует интуитивному разбиению множества деталей, изображенному на рис.3.13

Для формирования кода типового представителя какого-либо класса деталей необходимо поделать следующее. Возьмем, для примера третий класс.

1.Выполняем покомпонентное сложение векторов, соответствующим деталям этого класса

F(a₄)=[01000000100]

F(a₅)=[01000000100]

F(a₇)=[01000000101]

F(a₄ a₅ a₇)=[03000000301]

2.Выполняем алгебраическое сложение чисел в компонентах результирующего вектора

∑=7

Среднее значение 7/3=2.3

3.Формируем вектор состава признаков класса деталей. Он будет

∑*=[01000000100]

Таким образом, к этому классу относятся детали ограниченные наружными цилиндрическими ступенчатыми поверхностями и имеющие снаружи выступ.

Типовые и групповые процессы послужили основой для создания методов автоматизированного проектирования. Этому способствовало отсутствие методов проектирования на ЭВМ индивидуальных технологических процессов. Однако использование только типизации и групповой технологии не принесло ожидаемого эффекта от применения ЭВМ, так как эти методы требуют больших затрат времени на подготовку качественно новых типовых и групповых процессов и большого объема ИПС для их хранения. Заимствование у архивов предприятий типовых и групповых технологических процессов как метод комплектования ИПС АС ТПП, широко применявшийся в первый период разработки АС ТПП первого поколения не мог быть рекомендован, так как ориентирует на пройденные этапы развития и методов проектирования.

Работы по созданию теории и методов автоматизированного проектирования индивидуальных технологических процессов позволяет говорить об автоматизированных системах технологического проектирования второго поколения. В этом случае в системе предусматривается проектирование и исполнения индивидуальных технологических процессов с последующим их анализом, классификацией и группирования по принципу единства технологии и оснастки.