17. Принципы построения моделирующих алгоритмов.

Принципы построения моделирующих алгоритмов:

• с постоянным шагом во времени (принцип ∆t)

• по особым состояниям (событиям) (принцип δz)

Обобщенный алгоритм моделирования с постоянным шагом во времени:

Достоинства:

1) Простота реализации

2) Удобство при большом числе событий

Недостатки:

1) Нерационально затрачиваются ресурсы при редких событиях

2) Сложность выбора шага изменения времени

3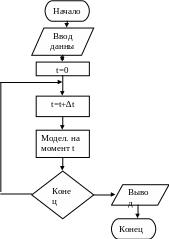 ) Появление ошибок в отображении процессов в связи с дискретными моментами времени.

Обобщенный алгоритм моделирования по событиям

Достоинства:

1) Сокращение объема вычислений при редких событиях

2) Более точное отражение процессов во времени

Недостатки:

1) Усложнение алгоритма за счет необходимости определения времени наступления наиболее раннего события.

18. Сущность метода статистического моделирования

Задачи, решаемые методом статистического моделирования:

• моделирование процессов на протекание которых влияют случайные величины

• решение математических задач, не связанных со случайностями, но для которых можно искусственно придумать вероятностную модель (вычисление площади).

Особенности метода статистического моделирования:

• простая структура вычислительных алгоритмов (составляется алгоритм для одного испытания и повторяется много раз)

• метод дает приближенный результат, ошибка вычисления пропорциональна 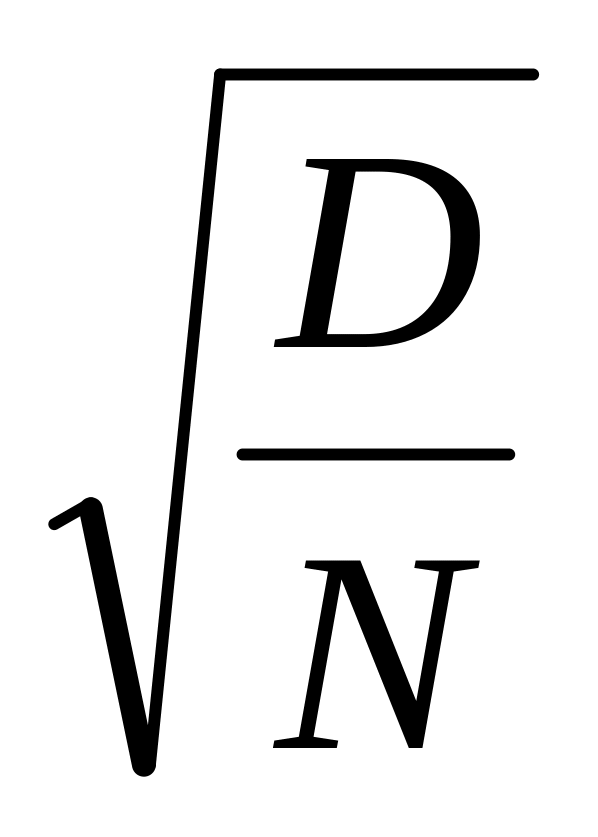(D-const, N-кол-во испытаний).

Сущность метода:

Метод статистического испытания заключается в воспроизведении сложных случайных явлений при помощи статистической модели, функционирование которой подчиняется тем же законам, что и исследуемые случайные явления.

Под статистической моделью понимается такая математическая модель, в которой сложные случайные явления с неизвестными вероятностными характеристиками и законами распределения заменяются простыми случайными величинами и событиями, вероятностные характеристики и законы распределения которых известны.

Метод основан на многократном проведении испытаний построенной модели с последующей статистической обработкой полученных данных с целью определение характеристик рассматриваемого сложного случайного явления в виде статистических оценок его параметров, случайный результат, полученный при проведении каждого испытания, называется реализацией.

Пр. Требуется определить функцию распределения случайной величины если известны:

• зависимость y=F(a,b,…,w)

• функции распределения величин a,b,…,w

1.По каждой из величин a,b,…,w проводится случайное испытание и определяются их случайные значения.

2.Используя полученные величины определяем y

3.N раз повторяем

4.на основе N значений y находим функцию распределения

19. Способы формирования случайных чисел. Аппаратный и физический.

При статистическом моделировании систем одним из основных вопросов является учет стохастических воздействий. Количество случайных чисел, используемых для получения статистически устой­чивой оценки характеристики процесса функционирования системы S при реализации моделирующего алгоритма на ЭВМ. Количество случайных чисел колеблется в достаточно широких пределах в зависимости от:

1 класса объекта моделирования;

2.вида оцениваемых характеристик;

3необходимой то­чности и достоверности результатов моделирования. Результаты статистического моделирования существенно за­висят от качества исходных (базовых) последовательностей случай­ных чисел.

На практике используются три основных способа генерации случайных чисел:

• аппаратный (физический);

• табличный (файловый);

• алгоритмический (программный).

Аппаратный способ. Генерация случайных чис­ел вырабатываются специальной электронной приставкой — генератором (датчиком) случайных чисел,— служащей в качестве одно­го из внешних устройств ЭВМ. Реализация этого способа генерации не требует дополнительных вычислительных опе­раций ЭВМ по выработке случайных чисел, а необходима только операция обращения к внешнему устройству (датчику). В основе лежит физический эффект, лежащего в основе таких генераторов чисел, чаще всего используются шумы в электронных и полупроводнико­вых приборах, явления распада радиоактивных элементов и т. д.

Достоинства:

Запас чисел не ограничен;

Расходуется мало операций;

He занимается место в памяти .

Недостатки:

Требуется периодическая проверка;

Нельзя воспроизводить последовательности;

Используется специальное устройство;

Необходимы меры по обеспечению стабильности.

Табличный способ. Случайные числа, представленные в виде таблицы, помещаются в память ЭВМ. Этот способ получения случайных чисел обычно используют при сравнительно небольшом объеме таблицы и файла чисел.

Достоинства:

Требуется однократная проверка;

Можно воспроизводить последовательности.

Недостатки:

Запас чисел ограничен;

Много места в ОЗУ;

Необходимо время для обращения к памяти.