46 Содержание обработки результатов экспериментов.

Основное содержание обработки результатов экспериментов:

1. Вычисление оценок параметров исследуемых величин

2. Исключение грубых ошибок измерений

3. Оценка точности и достоверности результатов моделирования

4. Проверка статистических гипотез

5. Построение регрессионных зависимостей, оценка их качества

6. Анализ полученных результатов

Требования к оценкам характеристик случайных величин

Состоятельность, несмещенность, эффективность

Оценка – состоятельная, если она при неограниченном увеличении числа опытов сходится по вероятности к математическому ожиданию параметра

Оценка – несмещенная, если ее математическое ожидание при любом конечном N равно истинному значению параметра

Оценка – эффективная, если среди всех возможных она обладает наименьшей дисперсией

Оценка математического ожидания x_i- значение параметра в i-ом испытании

Оценка дисперсии

Оценка среднего квадратического отклонения

Дисперсия оценки математического ожидания

Оценка корреляции двух случайных величин

Корреляционный момент:

Коэффициент корреляции

Оценка вероятности

Дисперсия оценки вероятности

Методы исключения грубых ошибок измерений

1. Правило трех сигм

2. Использование доверительного интервала

47 Оценка точности и достоверности результатов моделирования.

Правило трех сигм: Разброс случайных величин от среднего значения не должен превышать

Вычислить оценки величин, не включая в расчеты сомнительные значения, а затем проверить, попадают ли сомнительные значения в указанный интервал. Поскольку результаты, получаемые методом статистического моделирования, неизбежно носят случайный характер, после обработки результатов моделирования требуется ответить на вопросы:

1. К каким ошибкам может привести замена параметра случайной величины его точечной оценкой? (т.е. какова точность полученных результатов)

2. С какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы? (т.е. какова достоверность полученных результатов)

, где -точность оценки

- Достоверность оценки – вероятность того, что ошибка не выйдет за заданные пределы

С вероятностью неизвестное значение параметра попадет в интервал

Доверительная вероятность доверительный интервал

Построение доверительного интервала для математического ожидания

Случайная величина представляет собой сумму N независимых одинаково распределенных случайных величин и в силу центральной предельной теоремы распределена по нормальному закону.

;

функция распределения для нормально распределенной случайной величины с параметрами m=0, =1 ; Величина определяет для нормального закона число средних квадратических отклонений, которое нужно отложить вправо и влево от центра рассеивания для того, чтобы вероятность попадания в полученный участок была равна

Требуемое число реализаций для обеспечения заданной точности математического ожидания

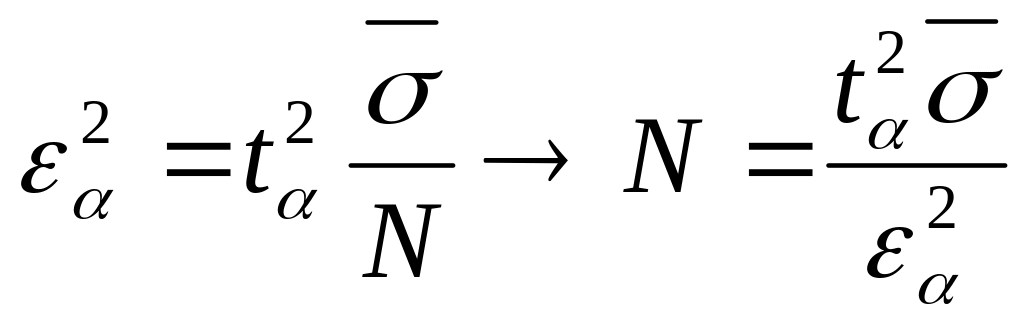
Определение количества реализаций моделирования в каждом опыте

1. проводится предварительный эксперимент с количеством измерений N’, которое составляет в зависимости от трудоемкости опыта от 20 до 50;

2. вычисляется среднеквадратичное отклонение ( точнее ее оценка);

3. в соответствии с поставленными задачами эксперимента устанавливается требуемая точность измерений ;

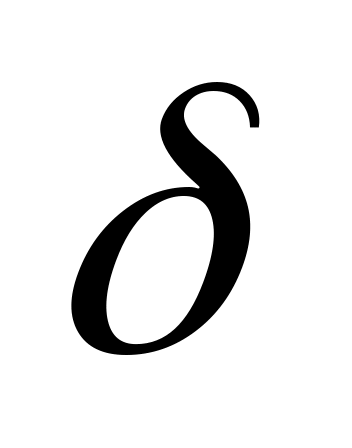4. устанавливается нормированное отклонение , значение которого обычно задается (зависит также от точности метода), по формуле определяют N