Вопрос 7. Экономическое содержание двойственности. Способы получения и практическое использование оценок ресурсов и их св-ва: оценка как мера влияния на функционал.

Рассм модель оптимизации пр-ва по критерию max дохода (при использовании для производства i-й продукции одного технологического способа производства T_i (i = 1,2,..., n)).

p_i — доход от реализации продукции, изготовляемой однократным применением i-й технологии.

a_ij — затраты j-го ресурса ( j =1,2,..., т) при однократном применении i-й технологии.

Состояние производственной системы задается вектором интенсивностей использования технологий Т₁,..., Т_n.

Вектор “выпуск-затраты”, описывающий функционирование производственной системы, имеет вид .

При этом выпуск товарной продукции равен ,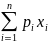

а затратыi-го ресурса составляют величину .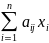

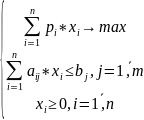
Рассмотрим модель с т зрценности имеющихся у предприятия ресурсов.

Каждый вид ресурса обладает некоторой “теневой ценой”, определяющей ценность ресурса с т зр дохода от реализации выпускаемой продукции. Она зависит от наличного запаса ресурса и потребности в нем для выпуска продукции.

Экономический результат совпадает с затраченными ресурсами, исчисленными в их теневых ценах.

Оптимальные теневые цены называют объективно обусловленными оценками (о.о.о.) или оптимальными оценками, или двойственными оценками ресурсов.

Для определения о.о.о. ресурсов составим самостоятельную задачу ЛП.

• Обозначим через 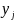( j=1,2,..., m) о.о.о.j-го ресурса.

• Величины должны быть такими, чтобы сумма теневых цен ресурсов, затрачиваемых при любом используемом производственном способе, не была меньше величины дохода :

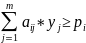
• Если произв. система в оптимальном состоянии, то ресурсы потребляются в соответствии сихо.о.о., а их суммарная теневая цена - наименьшая возможная

Модель:

1 и 2 теоремы двойственности:

1. равенство экстремальных значений целевых функций:

2. свободные переменные в оптимальном решении прямой задачи (принимают нулевое значение) соответствуют базисным переменным оптимального решения двойственной задачи (принимают положительные значения), и наоборот.

Соотношения “дополняющей нежесткости”:

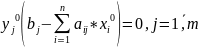
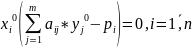
Краткая экономическая интерпретация соотношений:

1. в оптимальном состоянии суммарный выпуск предприятия совпадает с затратами производственных ресурсов, исчисленными в их теневых ценах.

2. Первое из соотношений показывает, что, если j-й производственный ресурс является недефицитным (т.е. выражение в круглых скобках строго положительно), то его теневая цена равна нулю. Наконец, второе из соотношений показывает, что если i-й производственный способ является интенсивным, т.е. , то величина выпуска совпадает с затратами производственных ресурсов по этой технологии.

Экономическая интерпретация двойственных оценок:

• Для продуктов – это упущенная выгода в случае включения данного продукта в производственную программу (насколько уменьшится совокупный выпуск, если мы решим отвлечь недефицитные ресурсы на выпуск 1 ед. этого продукта);

• Для ресурсов – предельная отдача ресурсов (насколько увеличится совокупный выпуск при увеличении данного ресурса на 1 ед.).

Свойства двойственных оценок: