Вопрос 3.Метод имитационного моделирования (мим) применительно к задачам систем управления запасами.

Классическая модель управления запасами:

D – годовое потребление;

Cп – стоимость единицы продукции (включает составляющие, зависящие от количества товара);

Co – составляющая расходов на поставку, которая не зависит от количества товара;

Ch – годовые издержки хранения;

q – объем партии товара (размер запаса);

T – период повторения заказа (время между поставками).

Задача – построить модель и оптимизировать ее.

Будем считать, что спрос равномерен.

- Формула оптимального размера заказа

• Число 2 мы можем не писать в формуле, если у нас зарезервированы места на складе

Но! Эта формула (Уилсона – Харриса) была выведена давно и не учитывалась временная стоимость денег. А мы учтем:

Рассматриваем метод Монте-Карло, моделируем модель управления запасами, хотим получить величину спроса на товар.

За год, зная годовое потребление (спрос), необходимо минимизировать затраты. Модель разыгрываем столько раз, пока не получим идеал.

Минусы: перебор (иногда может длиться очень долго).

Имитационное моделирование — это метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику.

Цельимитац. эксперимента: проверка выдвинутой гипотезы, оценка реакции моделируемой системы на то или иное воздействие, выявление влияния случайных возмущений на ход процесса и т.д. Далее строится модель, связывающая эндогенные переменные с ее управляющими и экзогенными переменными (напр.: в виде показателей, представленных временными трендами).

В узком смысле подИМ понимают имитацию поведения системы путем воспроизведения взаимодействий ее элементов между собой и с внешней средой (метод Монте-Карло). Структура связей модели предполагается заданной. По сути это модели «черного ящика». Решения получаются в ходе эксперимента в виде конкретных количественных характеристик.

Метод Монте-Карло – это численный метод решения математических задач, ответ на которые формируется в виде числа, а процесс решения основывается на моделировании, разыгрывании случайных величин.

Используется, когда необходимо определить, какое воздействие оказывает неопределенность исходных данных на поведение модели.

Суть:

Производим изделия. Для их производства необходимы детали, которые закупаются у поставщика. Спрос на детали оценивается от x1 до xn. Частота спроса на аккумуляторы показана в таблице – за несколько недель:

Спрос в неделю	Частота
х1	a1
…	…
хn	an

Начальный запас деталей составляет q шт.

Произв-ся подача заказов на партии деталей размером в c шт., когда их запас опускается ниже уровня в q0 шт.

Интервал времени между подачей заказа и осуществлением поставок в таблице:

Время поставки заказа, неделя	1	2	3	4
Вероятность	p1	p2	p3	p4

Единичная стоимость хранения запасов в неделю задана, рассчитывается для общего размера запаса, оставшегося на конец недели.

Стоимость заказа известна,

отсутствие деталей на складе оценивается в aруб./нед.

Задача: оценить средние издержки.

Решение.

• строим ф-ю распредобъема спроса в неделю и интервалы случайных чисел для значений стохастической переменной (4 и 5 столбцы)

  Спрос в неделю	Частота	Вероятность	Значение функции распределения	Интервал случайных чисел
  х1	a1	p1= a1/сумм	f1=p1	от	1	до	f1
  …	…	…	…
  хn	an	pn= an /сумм	fn=p1+…+pn=1	от	fn-1 +1	до	fn
  	=сумм	=1

• строим ф-ю распред и интервалы случайных чисел для времени выполнения поставок:

Время поставок	Вероятность	Значение функции распределения	Интервал случайных чисел
1	p1	f1=p1	от	1	до	f1
4	p4	fn=p1+p2+p3+p4=1	от	fn-1 +1	до	fn
Итого	1

Процесс имитации:

1. Каждая имитируемая неделя начинается с проверки, поступил ли сделанный заказ. Если заказ выполнен, то текущий запас увеличивается на величину заказа c шт.

2. Путем выбора случайного числа генерируется недельный спрос для соответствующего распределения вероятностей.

3. Рассчитывается итоговый запас = исходный запасq - величинаспроса. Если q недостаточен для удовлетворения недельного спроса, спрос удовлетворяется, насколько это возможно.Фиксируется число нереализованных продаж.

4. Определяется, снизился ли запас до точки восстановления d шт. Если да, причем не ожидается поступления заказа, сделанного ранее, то делается заказ.

Определим средние издержки в неделю:

• ст-сть заказов= Затраты на один заказ х Среднийспрос.

• стоимость хранения = Затраты на хранение единицы в нед х Средняя величина конечного запаса.

• стоимость упущ продаж = Стоимость упущ продажи х Среднее число упущ продаж в неделю.

средние издержки в неделю=Стоимость заказов + Стоимость хранения + Стоимость упущ продаж

Дискретные СВ:

Строим последовательность, удовлетворяющую условиям 1 и2, каждая запись состоит из известных ξ₁,…, ξ_n с вероятностями p₁,…,p_n

Алгоритм:

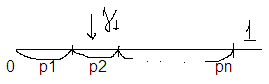
1. γ, γ<p₁ =>ξ₁, если нет то 2

2. γ<p₁+p₂ =>ξ₂

3. γ<p₁+p₂+p₃ =>ξ₃и тд

Так как ξ распределена равномерно на (0, 1), то вероятность попасть на интервал из (0, 1) равна длине интервала.

Непрерывные СВ

F(x) - Функция распределения

f(x) - Плотность распределения

Свойства:

1. Случайность

2. Независимость

3. Соответствие ЗР: для любого (t₁, t₂) P{t₁<запись <t₂}=F(t₂)-F(t₁)=

F(ξ)= γ, γ€R(0, 1)

γ – СВ, так как 1 и 2 выполняются

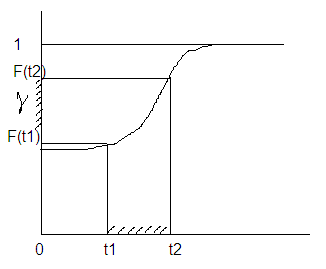
Вероятность, что γ €(t₁, t₂) равна длине интервала

Моделирование многомерных случайных величин.

Рассмотрим на примере двумерных величин. Разыгрывание сводится к разыгрыванию её составляющих.

Дискретный ЗР

• Если х и у независимы, то находится ЗР каждой из составляющих, которая затем разыгрывается как одномерная, не зависимо от другой.

• Если х и у зависимы, то находится ЗР одной составляющей и условный ЗР другой.

Непрерывный

• Если х и у независимы, то находится ЗР любой из составляющих и разыгрывают произведение методом обратной функции.

• Если х и у зависимы, то находится ЗР одной составляющей и условный ЗР другой.

Рассмотрим моделирование непрерывной векторной СВ .

Ее полное описание задается совместной плотностью ,

Стандартный метод моделирования векторных СВ основан на представлении w(x) в виде произведения

.

вектор может моделироваться покомпонентно:

• ξ1 с ПРВ ,

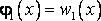• ξ1 по ПРВ 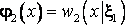и т. д.

• Последней ξm , имеющая ПРВ .

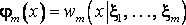После каждая компонента моделируется как скалярная величина

Оценка точности решения имитационных задач.

Оцениваем точность полученного результата, после моделирования СВ следующим образом: определяем необходимый объем выборки для заданной точности. Используем ЦПТ:

Если n ->∞ , то ->0 а значит, ошибка не превышает

Чтобы найти заданную точность