Вопрос 27. Основные понятия теории линейного программирования. Теоретические основы симплекс-метода.

Задача ЛП – однокритериальная задача условной (с ограничениями) оптимизации с линейным функционалом и линеными ограничениями.

Примерами задач ЛП могут служить задачи о фанерном цехе, о составлении рациона, классическая транспортная задача, динамическая задача планирования производства.

1. решение задачи ЛП находится на границе допустимого множества;

2. множеством решений может быть: ø, точка, отрезок, луч, прямая.

3. Если решение достигается, то это присходит в одной крайних точек.

В силу конечности крайних точек, задача сводится к их перебору.

4. Хотелось бы от общего перебора перейти к направленному, например, с постоянным улучшением функционала.

Во всех случаях задача ЛП сводится к стандартной

Каноническая(для нее симплекс-метод)

Общая

m – количество ограничений, n – количество переменных, n>m.

, x_b – базисные, x_s – свободные.

– базисные столбцы.

– свободные столбцы.

Если x_s= 0, – базисное решение.

Базисное решение может оказаться недопустимым.

Теорема. Если множество допустимых значений задачи ЛП не пусто, то в нем  хотя бы одно базисное решение.

Теорема. Множество допустимых базисных решений задачи ЛП совпадает множество крайних точек допустимого множества решений этой задачи.

Теорема. Если задача ЛП имеет решение, то оно достигается хот бы в одной из крайних точек.

Симплекс метод.

Предполагается, что есть допустимое базисное решение – x_bx_s(базисные и свободные компоненты этого решения).

Из предыдущего можно отметить, что . Функционал тоже можно разделить на c_bи c_s.

– симплекс разности.

Важные выводы:

1. если все симплес разности  0, то значение целевой функции улучшить нельзя, то есть перед нами решение задачи;

2. не базисный столбец a_j имеет смысл вводить в базис, если симплекс разность > 0;

3. можно выбирать наибольшую из положительных симплекс разностей d_j.

Пусть a_r – столбец, который было решено ввести в базис.

 из-за того, что остальные из свободных переменных останутся свободными.

.

l

l – это одна из базисных переменных, индекс той переменной, которая реально выводится из базиса.

Значение x_l = 0 для этого нового базиса.

Сам симплекс метод сводится к следующему:

1. Имеем базисное решение. Для него формируем A_b, A_s, C_b, C_s, X_b, X_s.

2. Вычисляем сиплекс разности. Если все они  0, получено решение, конец процедуры. Если нет, вводим в базис столбец a_r.

3. Если , то функционал можно увести в +, а если нет – .

4. Вычисление нового базисного решения

5. Переход к 1.

Вопрос 28. Статическая межотраслевая модель в. Леонтьева. Основные соотношения.

Статистические межотраслевые модели используются для разработки планов выпуска и потребления продукции и основываются на соотношениях межотраслевого баланса.

предположения:

1. каждая отрасль производит один продукт;

2. в каждой отрасли имеется единственная технология производства;

3. нормы производственных затрат не зависят от объёма выпускаемой продукции;

4. не допускается замещение одного сырья другим.

обозначения:

- общий (валовой) объем продукции i–й отрасли (i = 1..n);

- объем продукции i-й отрасли, потребляемой j-й отраслью в процессе производства (i,j = 1,2,…,,n);

- объем конечного продукта i-й отрасли для непроизводственного потребления.

величина xij может быть представлена следующим образом:

aij называется коэффициентом прямых материальных затрат (КПЗ).показывает, какое количество продукции i-й отрасли идет на производство единицы продукции j-й отрасли. постоянные.

Модель:

в матричном виде:

X = (x1, x2, ..., xn) - вектор валовых выпусков;

Y = (y1, y2, ..., yn) - вектор конечного продукта;

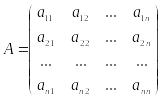- матрица коэффициентов прямых материальных затрат.

Интерпретируя выражение АХ как затраты, эту систему часто называют моделью «затраты выпуск».

КПЗ являются основными параметрами статической межотраслевой модели. Их значения могут быть получены двумя путями:

1. Статистически.на основе анализа отчётных балансов за прошлые годы.

2. Нормативно. Предполагается, что отрасль состоит из отдельных производств, для которых уже разработаны нормативы затрат; на их основе рассчитываются среднеотраслевые коэффициенты.

Свойства КПЗ