3. Методы порогов сравнимости

Использование бинарных отношений между анализируемыми вариантами решений или альтернатив. Бинарные отношения соответственно определяют условия, при которых:

1) один вариант решения превосходит другой;

2) оба варианта решений эквивалентны;

3) оба варианта решений несравнимы между собой.

При изменении условий меняется и количество сравниваемых альтернатив. При этом изменяется и состав так называемого ядра, состоящего из альтернатив, оказавшихся не худшими при всех сравнениях.Реализация методов основана на использовании численных методов для оценки функций от нечетких/случайных величин без применения методов Монте-Карло.

Вопрос 25. Модель факторного анализа, критерии качества структуры модели. Использование результатов факторного анализа в регрессионных моделях

Для изучения сложных социально-экономических систем возможно использование методов факторного анализа, так как они позволяют

-сократить размерность признакового пространства;

-вскрыть скрытые причинно-следственные связи.

Использование факторного анализа дает следующие преимущества:

• Снижение признакового пространства, ;

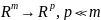• Лучшая интерпретация результатов исследования;

• Выявление и анализ структуры изучаемого процесса;

• Сжатия большого массива информации без потери содержательного наполнения признаков.

ФА предполагает разложение ф-ров на

• Общие

• характерные

модель:

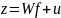
z – вектор стандартизированных элементарных признаков;

f – вектор общих факторов размерности k<m,

W – матрица факторных нагрузок размерности k*m;

u – характерность.

В отличие от МГК не утверждается, что наблюдаемые признаки могут быть однозначно вычислены (без потери информации) по значениям общих факторов f.

Остаток, не объясненный общими факторами, называется характерностью (u) и интерпретируется как влияние специфичных для каждого признака факторов и случайных ошибок.

1. Для определения коэффициентов модели фа

вычисляем ковариационные матрицы левой и правой частей векторного уравнения

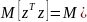
предположения:

1. Общие факторы стандартизированы и декоррелированы 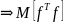является единичной матрицей;

2. Характерные и общие факторы независимы ;

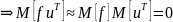3. Характерные факторы декоррелированы 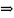ковариационная матрица 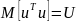является диагональной

Тогда уравнение для ковариаций преобразуется к компактному виду:

где R – корреляционная матрица элементарных признаков,

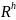- редуцированная корреляционная матрица (т.к. матрица U – диагональная, то элементы матрицы вне диагонали равны соответствующим элементам матрицы R)

Диагональные элементы редуцированной матрицы называются общностями и обозначаются как 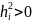. Качественно общность обозначает вклад общих факторов в полную дисперсию признака: .

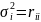Остаток – характерность.

определение общностей:

• Метод наибольшей корреляции

Мощности 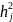присваивается наибольшее значение элемента столбца (строки) матрицы R кроме диагонального элемента матрицы R, равного единицы

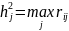
• Метод триад используется, когда матрица частных корреляций сильно отличается от матрицы парных корреляций (R)

При данном методе в j-й строке (столбце) матрицы R отыскиваются 2 наибольших значения коэффициентов корреляци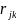и и и составляется триада

если вдруг , тогда ставим значение = 1

• Метод малого центроида

На главной диагонали матрицы R ставятся наибольшие коэффициенты корреляции каждой строки (столбца). По новой матрице вычисляется отношение квадрата суммы элементов соответствующей строки (столбца) к сумме всех элементов матрицы:

Цель расчета – методы направлены на увеличение относительного веса в факторной структуре признаков с сильными корреляционными связями и уменьшение связи слабо коррелируемых признаков.