Вопрос 24. Методы стохастической многокритериальной оптимизации

Нужно для управления сложными системами. Особенность именно стохастической оптимизации – все переменные не детерминированные, а случайные (спрос, курсы валют, курсы акций). Детерминированные – запланированные затраты, инвестиции. Разница в том, что здесь мы максимизируем или минимизируем матожидания, квантили, отклонения – смотря что нас интересует. Соотвественно переменные тоже в виде матожиданий и тд представлены. В остальном методы такие же, как для детерминиированных процессов (в последнем вопросе):

Постановка задачи:

Пусть имеются критерии .

Требуется найти точку , которая в некотором смысле минимизирует все эти критерии. Критерии называют частными критериями.

В совокупности они образуют векторный критерий , который и полежитоптимизации.

задача:

при условии .

Обычно нет решения, минимизирующего все частные. =>нужно искать компромиссное решение. Их стараются найти в классе так называемых эффективных решений (множество Парето).

Множество Парето – общее у всех. Как его найти?

1. g⁽¹⁾(x)->max => 1/ g⁽¹⁾(x)->min (все задачи необходимо сводить на мин.)

2. g⁽²⁾(x)->min

3. …

Нужно найти наилучшее решение х1…хn, которое минимизирует все эти функции.

Решение называется Парето оптимальным, если нельзя улучшить показатель хотя бы одного критерия, при этом чтобы не ухудшились показатели другого критерия. Необходимо использовать прямые методы: задача должна сводиться к однокритериальной.

Бывает несколько парето-опт. Тогда необходим доп. перебор эфф. решений. Приёмы:

• методы сведения задач многокритериальной оптимизации к задачам скалярной оптимизации;

• методы компенсации;

• методы порогов сравнимости.

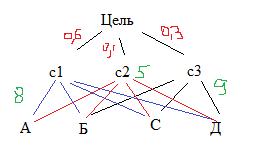
Метод аналитической иерархии. Общая схема МАИ. Постановка задачи:

1.Задана общая цель (n), назначена соответствующая система, которая должна оптимизироваться.

2. Задано произвольное число альтернатив, из которых нужно выбрать лучшее

3. Задано произвольное число частных критериев, по которым анализируются эти альтернативы.

Требуется найти наилучшую альтернативу. Атрибуты:

1. Н а первом шаге задача оптимизации структурируется в виде соответствующей иерархии ( цели, критерии и альтернативы).

2. Реализация попарных сравнений для элементов каждого уровня с учетом специфики требований элементов более высокого уровня иерархии. При этом результаты попарных сравнений реализуются в виде матрицы, по которым затем определяется веса важности этих элементов

3. Определяются количественные индикаторы альтернативы, называемые приоритетами.

Шкала сравнений: 1.Эквивалентны(1) 2.Умеренное превосходство (3-1) 3.Существенное превосходство (5-1) 4.….(7-1) 5.….(9-1)

Матрица сравнений сравнивает каждый элемент с каждым:

	А	Б	С	Д	сумма	Нормируем	Итог
А	1	2	3	6	12	1/2	1*1/2+2*1/4+3*1/6+6*1/12=2
Б	1/2	1	3/2	3	12/2	1/4	1
С	1/3	2/3	1	2	12/3	1/6	4/6
Д	1/6	1/3	1/2	1	12/6	1/12	4/12
сумма					24	1

Свойства матрицы:

• a_ii=1, для любых i

• aij=1/aji =>aij*1/aji=1 – обратно симметричная матрица

• aik*akj=aij

• vi/vk*vk/vj=vi/vj – согласованная матрица