3. Метод инструментальных переменных

Для получения несмещенных (по крайней мере состоятельных) оценок параметров эконометрических моделей в ситуациях, когда имеют место корреляционные взаимосвязи между независимыми переменными x_it и ошибкой _t.

Предположим, что существуют так называемые “инструментальные” переменныеz_i, число которых в общем случае совпадает с числом независимых факторов модели х_i, i=1,2,..., n;

при t=1,2,..., Т, каждая из которых характеризуется нулевыми корреляционными взаимосвязями с ошибкой эконометрической модели .

При заданномТ матрица значений инструментальных переменных Z имеет такой же размер, как матрица Х.

Умножим слева векторно-матричное уравнение на матрицу у=Х+на матрицу Z.

Получим Zу=ZХ+Z,

С учетом того, что M[Z]=0, умножая слева на (ZХ)^–1, непосредственно имеем a_z =(ZХ)^–1Zу, где a_z – вектор оценок параметров эконометрической модели, полученный с использованием инструментальных переменных.(состоятельные)

Вопрос 17. Аналитическое решение и графическое представление игры 2x2. Возможности и перспективы применения теории игр при решении соц-экон задач.

Задачатеорииигр – отыскание оптимальной стратегии поведения участников конфликта с цельюmaxвыигрышей или minпроигрышей.

Участники выбирают из нек-го числа альтернатив (чистых стратегий), каждая из к-х приводит к опред последствиям.

Простейший случай игры – 2х2 с нулевойсуммой, т е выигрыш одного игрока означает проигрыш другого.

Пример.

Пусть игра задана платежной матрицей

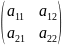
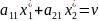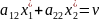Средний выигрыш первого игрока, если он использует оптималь­ную смешанную стратегию х* = (х*_{1 ,} х*₂), а второй игрок— чистую стра­тегию 1, равен це­не игрыv: . Если 2й игрок применяет стратегию 2, то . Приравниваем это и получаем сис­тему уравнений для определения оптимальной стратегии первого игрока и цены игры:

Решая эту систему, получим оптимальную стратегию и цену:

, ,

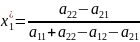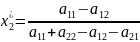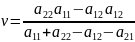
Так же для 2го игрока:

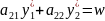
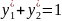
Графический метод

Для определенности, игрок I имеет возможность выбирать между двумя стратегиями с вероятностями p₁ и p₂ = 1-p₁.

в системе координат хОу на оси абсцисс откладывается отрезок А₁,А₂, равный единице, и через концы этого отрезка проводятся перпендикулярные к оси абсцисс прямые, на которых откладываются выигрыши игрока А.

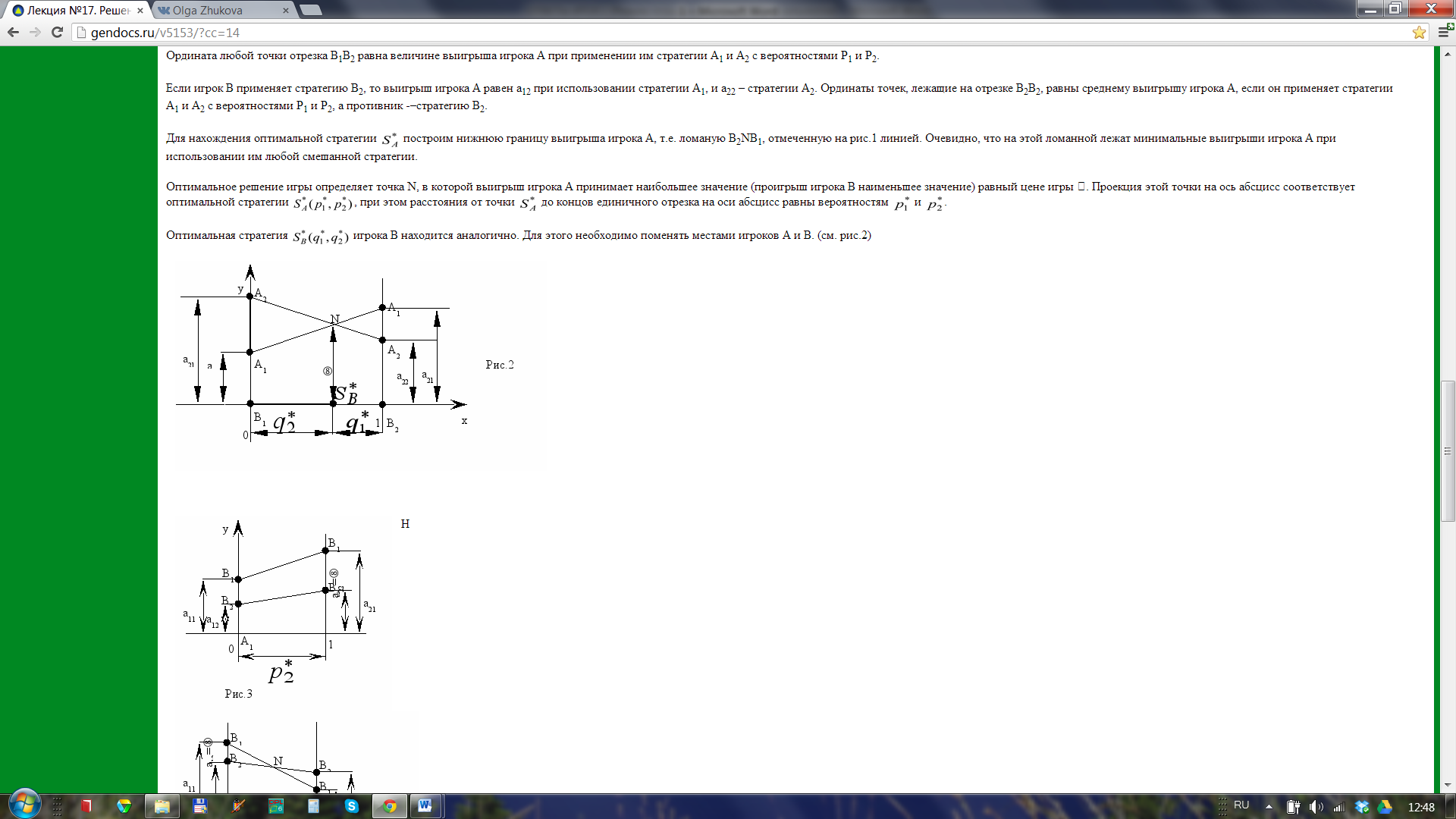
Левый перпендикуляр, совпадающий с осью ординат, соответствует стратегии А1, для которой Р1=1, Р2=0, а правый равен стратегии А2, для которой Р1=0, Р2=1. При применении игроком В стратегии В1 выигрыш будет а11, если игрок А использует стратегию А1, и будет а21, если он применяет стратегию А2. Отложив отрезки, равные а11 и а21 на соответствующих перпендикулярах получим две точки: В1 соответствующий стратегии А1 и В1 соответствующий стратегии А2. Ордината любой точки отрезка В1В2 равна величине выигрыша игрока А при применении им стратегии А1 и А2 с вероятностями Р1 и Р2.

Если игрок В применяет стратегию В2, то выигрыш игрока А равен а12 при использовании стратегии А1, и а22 – стратегии А2. Ординаты точек, лежащие на отрезке В2В2, равны среднему выигрышу игрока А, если он применяет стратегии А1 и А2 с вероятностями Р1 и Р2, а противник -–стратегию В2.

Для нахождения оптимальной стратегии построим нижнюю границу выигрыша игрока А, т.е. ломаную В2NB1, отмеченную на рис.1 линией. Очевидно, что на этой ломанной лежат минимальные выигрыши игрока А при использовании им любой смешанной стратегии.

Оптимальное решение игры определяет точка N, вкоторой выигрыш игрока А принимает наибольшее значение (проигрыш игрока В наименьшее значение) равный цене игры . Проекция этой точки на ось абсцисс соответствует оптимальной стратегии , при этом расстояния от точки до концов единичного отрезка на оси абсцисс равны вероятностям и .

Оптимальная стратегия игрока В находится аналогично. Для этого необходимо поменять местами игроков А и В. (см. рис.2)