Вопрос 16. Эконометрические модели с нестандартными ошибками

У нестандартных ошибок ковариационная матрица может быть отлична от диагональной матрицы Cov()_²Е, что является следствием:

• корреляционных взаимосвязей между ее разновременными значениями на интервале (1, Т),

• дисперсия ошибки может не обладать свойством постоянства, _²const (гетероскедастичность ошибки)

• ошибка  может быть связана с одной или несколькими независимыми переменными эконометрической модели х_i.

Нарушение условий приводит к тому, что оценки коэффициентов эконометрических моделей, полученные на основе “классических” методов МНК и ММП, теряют некоторые свои “качества”. Прежде всего, это относится к свойству эффективности оценок, полученных при ограниченных объемах выборки. Такая ситуация, заставляет нас искать определенные подходы, приемы получения “качественных” оценок параметров эконометрических моделей и при свойствах их ошибок, отличных от тех, которые были определены стандартными условиями.

Данные подходы и приемы обычно базируются на так называемых обобщенных методах оценивания – обобщенном МНК (ОМНК) и обобщенном ММП (ОММП), на использовании при получении оценок параметров моделей так называемых “инструментальных переменных”. Рассмотрим особенности этих подходов более подробно.

1. Обобщенный метод наименьших квадратов

ОМНК базируется на свойстве положительно определенной ковариационной матрицы , допускающей представление в виде произведения двух матриц: =,

где матрица — невырожденная.

^–1()^–1=Е,

()^–1^–1=^–1.

Предположим, что матрица известна. Умножим матрично-векторное уравнение исходной эконометрической модели у=Х+ слева на матрицу ^–1 и получим у_*=Х_*a+_*,

где у_*=^–1у; Х_*=^–1Х;_*=^–1.

Покажем, что ковариационная матрица вектора _* равнаЕ:

Cov(_*)=M[_*,_*]=M[^–1_*_*^–1]=^–1^–1=E. вытекает, что _²=1.

Модель:

у=Х+

Применяя к модели обычный метод наименьших квадратов, получим вектор оценки a из следующего выражения: a=(Х_*Х_*)^–1Х_*у_*=(Х^–1Х)^–1Х^–1у.

Оценки коэффициентов aобладают свойствами несмещенности и эффективности.

2. Обобщенный метод максимального правдоподобия

предполагается, что ошибка модели подчиняется нормальномуЗР, т. е. ()N(0, _).

В этом случае плотностьнормальногоЗР значений ошибки _t, t=1,2,... Т; можно представить в следующем виде:

()= _ _y^–1].)= (₁ ₂..._T)_ _^–1],

При этом ₁ =₂=...=_Т.

При независимых ошибках ₁, ₂,...,_{Т ,}()=

l= – 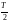ln(2) – ln_² – ln_– (у–Х)_^–1(у –Х).

Дифференцируя выражение по вектору параметров  и дисперсии ошибки _² и приравнивая нулю частные производные выражения для оценок параметров модели и ее дисперсии в следующем виде: a=(Х_^–1у)^–1Х_^–1у; _²= (у–Хa)_^–1(у –Хa).

Заметим, что с учетом равенства _=²_можно записать: a=(Х_^–1у)^–1Х_^–1у.

Оценки ОММП обладают свойствами асимптотической несмещенности, состоятельности и эффективности.